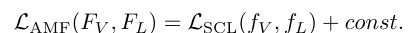논문 리뷰 - On the Generalization of Multi-modal Contrastive Learning

govlKH·2024년 8월 14일

목록 보기

40/45

논문의 (long) Preview + 사전 지식 Background

최근 다중 모달 대비 학습(Multi-modal Contrastive Learning, MMCL)은 시각적 작업에서 뛰어난 성능을 보여주며 많은 주목을 받고 있습니다. 본 논문에서는 MMCL이 시각적 표현을 어떻게 효과적으로 추출하는지에 대한 이론적 이해가 부족한 상황에서, MMCL의 일반화 성능을 이론적으로 분석하고, 기존의 자가 감독 대비 학습(Self-supervised Contrastive Learning, SSCL)과의 차이점을 설명합니다.

MMCL의 핵심 아이디어는 이미지와 텍스트 쌍과 같은 다중 모달 데이터를 함께 임베딩하여, 동일한 쌍의 샘플은 서로 가까워지도록 하고, 관련 없는 샘플은 멀어지도록 하는 것입니다. 그런데 이러한 MMCL이 어떻게 SSCL을 능가하는지에 대한 이론적 근거는 부족했습니다. 본 논문에서는 MMCL과 비대칭 행렬 분해(asymmetric matrix factorization, AMF) 사이의 내재적인 연결을 통해, MMCL의 시각적 하위 작업에 대한 일반화 보장을 처음으로 제시합니다.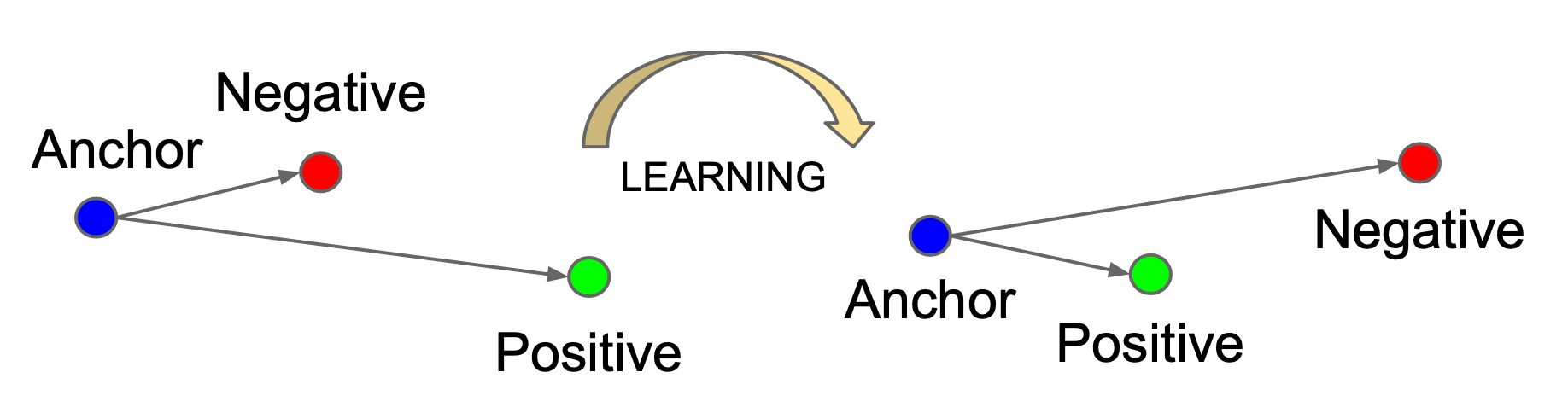

MMCL의 이론적 분석을 위해, 본 논문에서는 MMCL의 목적 함수와 multi-modal co-occurrence matrix의 Asymmetric Matrix Factorization 사이의 동등성을 구축하였습니다. 이 프레임워크를 바탕으로, MMCL과 SSCL을 통합하여 비교합니다. MMCL은 텍스트 쌍으로 유도된 양성 쌍을 통해 SSCL을 암묵적으로 수행하며, 이러한 관점에서 텍스트 쌍이 더 의미론적으로 일관되고 다양한 Positive Pair들을 유도하여 downstream task에서 일반화에 도움이 된다고 분석합니다.

MMCL이 SSCL보다 뛰어난 이유는 텍스트 쌍이 더 나은 의미론적 일관성과 다양성을 제공하기 때문입니다. 이러한 결과를 바탕으로, CLIP guided resampling methods를 제안하여, Multimodal 정보를 활용해 ImageNet에서 SSCL의 downstream task 성능을 크게 향상시킵니다.

특히, 본 논문은 MMCL과 SSCL의 차이를 통합된 관점에서 분석하고, 실제 데이터에서 텍스트로 유도된 Positive Pair들이 데이터 증강 기반의 Positive Pair들보다 더 나은 의미론적 일관성과 다양성을 제공함을 보입니다. 이 분석을 통해, Multimodal Positive Pair의 우수성을 입증하고, CLIP과 같은 사전 훈련된 모델을 활용하여 Self supervised Learning을 개선하는 방법을 제시합니다.

결론적으로, 본 논문에서는 다음과 같은 기여를 합니다:

다중 모달 대비 학습(MMCL)에 대한 첫 번째 일반화 이론적 보장을 제시하며, MMCL의 contrastive loss를 AMF 목표와 연결하여 새로운 관점을 제공합니다.

MMCL과 SSCL 간의 관계와 차이점을 통합된 관점에서 이해하며, Multimodal 정보가 Self supervised learning 보다 더 나은 Positive image pair들을 유도한다고 설명합니다.

CLIP과 같은 사전 훈련된 모델을 활용하여 Self supervised image learning을 안내하는 새로운 시나리오를 이야기하며, 이를 통해 ImageNet에서 성능을 개선하는 네 가지 기술을 제안합니다.

=> 즉, 이 연구는 Multi-Modal Contrastive Learning의 일반화 성능에 대한 새로운 이론적 이해를 제공하며, 실험적으로도 그 우수성을 입증함을 밝힙니다.

Asymetric Matrix Factorization이란?

비대칭 행렬 분해(asymmetric matrix factorization, AMF)는 데이터 분석 및 기계 학습에서 널리 사용되는 기술로, 특정 형태의 행렬을 두 개의 다른 행렬로 분해하여 원본 행렬의 구조적 특성을 이해하고 활용하는 방법입니다.

행렬 분해(Matrix Factorization)는 일반적으로 다음과 같은 목표를 가지고 있습니다:

데이터 차원 축소: 원본 행렬의 차원을 줄여서 효율적으로 분석하거나 저장할 수 있습니다.
특성 추출: 데이터의 잠재적인 구조나 패턴을 추출하여 더 깊이 이해할 수 있습니다.
예측 및 추천: 결측값을 예측하거나 추천 시스템에서 사용자와 아이템 간의 관계를 예측하는 데 사용됩니다.

비대칭 행렬 분해(AMF)의 특징:

비대칭 행렬: 비대칭 행렬은 원본 행렬이 비대칭인 경우를 말합니다. 즉, 행렬 $A$ 가 있을 때, $A \neq A^T$ 입니다.
분해 방식: AMF에서는 원본 행렬 $A$ 를 두 개의 다른 행렬 $U$ 와 $V$ 로 분해합니다. 보통의 경우, 원본 행렬 $A$ 를 다음과 같은 형태로 분해합니다: $A \approx U \cdot V$
여기서 UUU와 VVV는 각각 원본 행렬과 같은 차원을 가진 행렬입니다. $U$ 는 행(feature) 차원에 해당하고, $V$ 는 열(item) 차원에 해당합니다.
목표: AMF의 주요 목표는 원본 비대칭 행렬 $A$ 의 중요한 패턴이나 구조를 추출하는 것입니다. 이 과정에서 $U$ 와 $V$ 는 비대칭적인 구조를 반영하여 원본 행렬의 특성을 잘 설명하도록 학습됩니다.

응용:

추천 시스템: 영화 추천 시스템에서 사용자-영화 평점 행렬을 비대칭 행렬로 보고, 이 행렬을 분해하여 사용자와 영화 간의 잠재적 선호를 추출합니다.
정보 검색: 문서와 단어 간의 관계를 분석하여 문서 검색의 품질을 향상시키는 데 사용됩니다.
Multimodal 학습: 본 논문에서는 MMCL의 목적 함수와 AMF의 동등성을 구축함으로써, Multimodal 데이터의 패턴을 이해하고 시각적 표현을 추출하는 데 AMF를 활용합니다.
AMF는 데이터의 차원 축소와 패턴 인식에서 중요한 역할을 하며, 복잡한 데이터 구조를 이해하고 활용하는 데 강력한 도구라고할 수 있습니다.

3.1. Mathematical Formulation

본 논문에서는 멀티모달 대비 학습의 일반화 이론을 다룹니다. 여기서는 CLIP과 같은 멀티모달 대비 학습의 수학적 수식과 이론적 배경을 상세히 설명합니다.

수학적 공식화
멀티모달 대비 학습을 이해하기 위해, 기본적인 수학적인 공식들을 소개합니다. 예를 들어, CLIP을 고려해봅시다. 이 모델은 시각적 도메인과 언어 도메인에서 쌍을 이룬 데이터 $(x_v, x_l)$ 을 사용합니다. 여기서 $x_v$ 는 이미지를, $x_l$ 은 해당 이미지에 대한 텍스트 설명을 의미합니다. 각각의 $x_v$ 또는 $x_l$ 은 $r$ 개의 클래스 중 하나에 속합니다.

모든 시각적 데이터의 집합을 $X_V$ 로, 모든 언어 데이터의 집합을 $X_L$ 로 나타내며, 각각의 분포를 $P_V$ 와 $P_L$ 로 정의합니다. 이들의 결합된 멀티모달 분포는 $P_M$ 입니다. 간단히 설명하자면, $X_V$ 와 $X_L$ 은 매우 큰 유한 집합으로 가정하고, 각각의 크기를 $N_V = |X_V|$ 와 $N_L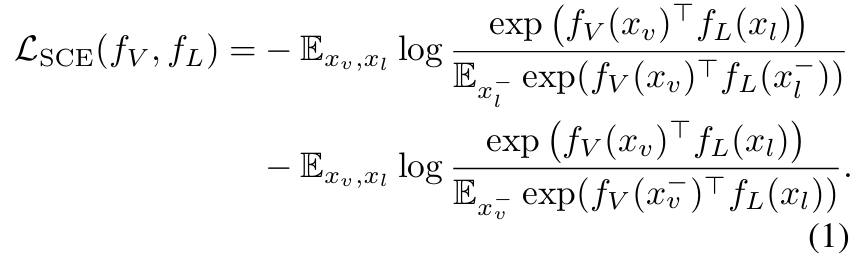 = |X_L|$ 로 정의합니다.

멀티모달 대비 학습의 목표는 시각적 데이터 $X_V$ 와 언어 데이터 $X_L$ 의 공동 임베딩을 $k$ -차원 잠재 공간 $\in \mathbb{R}^k$ 에서 얻는 것입니다. 이를 위해 시각적 인코더 $f_V : X_V \rightarrow Z$ 와 언어 인코더 $f_L : X_L \rightarrow Z$ 를 학습하여, 의미적으로 유사한 샘플들(이미지-이미지, 텍스트-텍스트 또는 이미지-텍스트 쌍)이 가까운 표현을 가지도록 하고, 서로 다른 샘플들은 멀리 떨어지도록 합니다.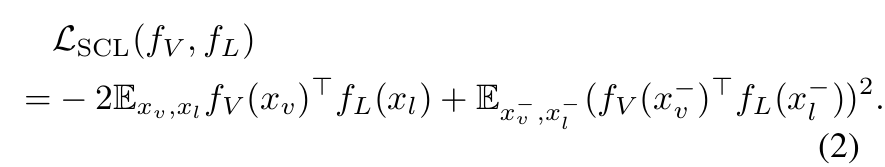
Pretraining이 진행된 후에는 linear proving을 기반으로 한 downstream tasks에 적용하는 방법을 살펴보겠습니다. 이는 딥러닝 모델에서 사전 훈련된 표현(즉, 학습된 임베딩 또는 특징)을 하위 작업에 적용하여 평가하는 방법에 대한 설명으로, 이를 하나씩 설명해 보겠습니다.

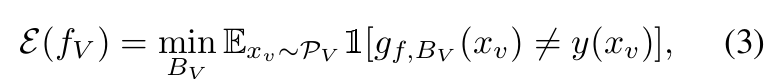
Linear Probing Task는 모델이 학습한 표현을 평가하는 한 방법으로, 주어진 특징에서 클래스 레이블을 예측하는 간단한 선형 분류기를 훈련시키는 것입니다. 위와 같이 추출된 feature에 기반하여 output을 linear embedding을 통해 뽑하네고, 이것이 실제 target과 같은지에 대하여 error값을 수식화한 것 입니다.

이 섹션에서는 다중 모달 대조 학습(MMCL)을 이해하기 위해, 이 방법을 비대칭 행렬 분해(AMF) 관점에서 분석해 보겠습니다. 기본적으로 MMCL의 목표는 시각적 데이터와 언어적 데이터의 임베딩을 학습하여 이들이 같은 의미를 가지는 쌍으로 가까이 배치되도록 하는 것입니다. 그러나 이렇게 개별 샘플 수준에서의 학습 목표가 전체 데이터의 분포에 어떤 영향을 미치는지에 대한 이해는 부족합니다. 본 논문에서는 MMCL의 목표를 재구성하여, MMCL이 실제로는 비대칭 행렬 분해와 본질적으로 동등하다는 것을 보여줍니다.

데이터 분포 $P_M(x_v, x_l)$ 를 시각-언어 데이터 쌍 간의 co-accurance matrix 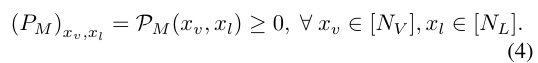$P_M \in \mathbb{R}^{N_V \times N_L}$ 로 표현합니다.

$P_M$ 은 a non-negative asymmetric matrix로 정규화 과정을 거쳐서 아래와 같이 Asymmetric Matrix Factorization관점에서 살펴볼 수 있습니다.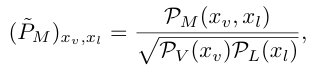

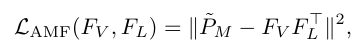
이제 저희는 이것과 함께 Theorem 3.1을 기반으로 어떻게 Contrasrtive Learning의 방법론이 AMF를 기반으로 해석될 수 있는 지 살펴보겠습니다.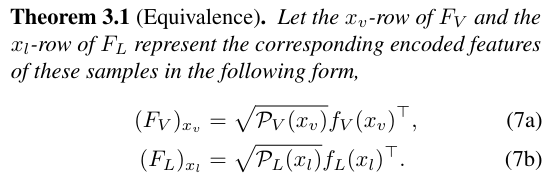

즉! 저희는 아래와 같은 식이 성립하는 지를 확인해 보겠습니다.

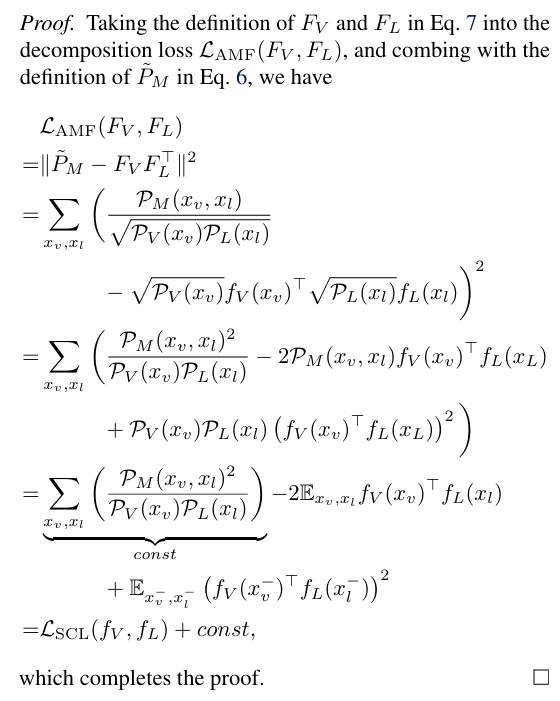
증명은 위와 같으며, 생각보다 큰 트릭은 없이 전개를 해 나가는 것을 확인할 수 있고, 저희가 원하는 식이 성립함을 확인해 볼 수 있습니다.

이 결과는 MMCL이 기본적으로 Co-accurance matrix의 저차원 분해를 학습하고 있음을 보여줍니다. 비대칭 행렬 분해는 원래의 Co-accurance matrix가 매우 크기 때문에 직접적으로 해결하기 어렵지만, MMCL은 이를 contrastive loss(InfoNCE loss)를 통해 효율적으로 계산할 수 있는 손실로 변환하여 문제를 해결합니다.

즉, 이는 이론적으로, 이 동등성은 AMF가 MMCL의 전체 분포를 특성화하고, downstream task에 대한 이상적인 표현에 대한 보장을 제공합니다. 왜냐하면 AMF에서의 행렬분해를 통해 시그마가 높은 값들만을 남긴다는 의미이며, 이것을 통해 저차원에서 대표하는 값들로 사용할 수 있다는 것 입니다!

Contrastive learning이 단순히 Positive Negative pair로만 학습해서 좋아 보이는 것 뿐 아니라, 대표하는 시그마들을 확실하게 가져올 수 있게 되기에 우수한 표현력이라는 것이 보장된다는 것 입니다!

Representation Learning과 Low-Rank Approximation의 연결

위 식은 멀티모달 데이터의 공동 분포를 정규화한 행렬 $\tilde{P}_M$ 를 낮은 차원의 행렬 $F_V$ 와 $F_L$ 의 곱으로 근사할 수 있다는 것을 의미합니다. 이 근사는 저차원 표현을 학습하는 과정에서 데이터의 중요한 구조를 캡처하는 데 유용합니다.

멀티모달 대조 학습의 목표는 두 도메인(예: 텍스트와 이미지) 간의 공통된 잠재적 표현을 학습하는 것입니다. 이는 비대칭 행렬 분해에서 $\tilde{P}_M$ 를 $F_V F_L^\top$ 로 근사하는 것과 동일한 목표를 가집니다.

손실 함수의 등가성

$L_{\text{AMF}}(F_V, F_L)$ 는 본질적으로 멀티모달 데이터 간의 관계를 나타내는 행렬을 저차원 표현으로 분해하는 과정에서의 오차를 측정합니다. 이 손실 함수는 멀티모달 대조 학습의 SCL 손실과 등가적이라는 것은, 멀티모달 대조 학습이 저차원 표현을 학습함으로써 데이터 간의 관계를 효율적으로 캡처하고 있음을 이론적으로 뒷받침합니다.

이는 멀티모달 대조 학습이 단순히 개별 샘플 간의 유사성을 학습하는 것이 아니라, 데이터 전체의 분포를 효과적으로 학습하고 있다는 의미를 지닙니다.

멀티모달 대조 학습의 일반화 성능

이 등가성은 멀티모달 대조 학습이 다양한 다운스트림 작업에서 잘 일반화될 수 있는 이유를 설명해줍니다. 저차원 표현을 통해 데이터의 핵심 구조를 학습함으로써, 새로운 데이터나 과제에도 효과적으로 적용될 수 있는 일반화된 표현을 얻는 데 도움이 됩니다.

결론적으로 이 식이 SCL 손실과 동일하다는 것은 멀티모달 대조 학습이 단순한 인스턴스 레벨의 학습을 넘어, 전체 데이터의 분포를 학습하는 저차원 근사로 해석될 수 있음을 보여줍니다. 이는 멀티모달 대조 학습의 이론적 기반을 확립하고, 이 방법이 다양한 실제 작업에서 좋은 성능을 보이는 이유를 설명하는 중요한 역할을 합니다.