이번 포스터에서는 Monte Carlo method에 대해 알아보겠습니다.
MC는 반복적으로 random sampling을 사용하여 수칙 결과를 얻는 것 입니다.
VAE 이해하기 위한 내용(3) - Monte carlo Algorithm
이를 참고하시면 이해가 수월할 것 같습니다.
강화학습은 Monte Carlo 방식입니다.
모든 RL은 tabular updating method을 사용합니다.
강화학습에서는 action value ft table :Q-table을 사용합니다.
model-free
MC policy Iteration은 기본적으로 GPI를 기본으로 합니다.
MC는 다른 강화학습과의 차이는 eposode-by-episode로 샘플을 얻어 진행한다는 점입니다.
결국 끝이 있어 끝나는 경우를 eposodic task 라고 하고, 끝나지 않는 경우를 continuous task 라고 합니다.
MC는 한 게임이 끝날 때 return을 가지고 진행하기에 episodic task입니다.
한 에피소드를 가지고 policy evaluation을 하고, 이것을 토대로 policy improvement를 하고, 또 새로운 에피소드를 가지고 policy evaluation을 하고를 반복합니다.
terminal까지 가는 backup이기에 multi step backup이라고 합니다.
Q ft을 estimate하는 방향으로 진행됩니다.
매 샘플로 주어진 에피소드마다 리턴값들을 얻고, 이들의 기댓값이 Q vlaue 를 계산하는데 사용됩니다.
강화학습을 하면 장점이 있는데, state space 내는 굉장히 방대합니다. 하지만 샘플로 진행되기에 state의 개수에 의존하지 않습니다. 손해보는 것 같지만 예를 들어 바둑과 같은 경우에 절대로 두지 않을 수들이 꽤 많습니다. 이런 경우들을 배제해주기에 효율적일 때가 많습니다.
MC의 장점은 Markov property가 깨져도 크게 영향을 받지 않습니다. MDP를 기본 모델로 지정하지만 Markov property를 충족하지 못해도 좋은 성능을 냅니다.
우선 boostrapping을 알아보겠습니다.
Q value는 Gt:true value를 사용하는 방법과 Rt+1 + 감마(St+1,At+1):estimate를 사용하는 방법이 있습니다. boostrapping은 이 두가지 방법 중 두 번째 방법을 사용하는 것을 말합니다.
MC는 첫 번째 경우를 사용하여 update를 진행하기에 boostrapping이 아닙니다.
Markov property는 past state은 영향을 미치지 않는다 입니다.
그런데 만약 이를 잘 충족하지 않는다면 두 번째 방법은 문제가 생깁니다. 현재 state을 가지고 다음 state을 말한다는 것이 정확하지 않게 됩니다.
따라서 두 번째 방법은 Markov property가 굉장히 중요합니다.
그에 반해 첫 번째 방법은 끝까지 간 후 return들의 평균입니다. 즉, 현재 state만 next state에 영향을 미친다는 Markov property가 조금 오차가 생겨도 게임을 끝까지 한 결과에 대해 진행하기에 크게 영향을 받지 않게 됩니다.
따라서 MC는 no boostrapping으로 Markov property를 조금 충족하지 못 하여도 괜찮다는 장점이 있습니다.
MC policy iteration 안에 있는 policy evaluation에 대해 알아보겠습니다.
이는 정확한 계산이 아니기에 Policy prediction이라고도 합니다.
목표는 current policy 안에서 경험을 한 real experience가 있을 것 입니다. 그런 entire episode가 있을 때 true Q value ft을 학습하는 것 입니다. 근사치로 찾아가는 것 입니다.
MC는 무조건 끝나는 게임이어야 하기에 terminal이 존재합니다.
여기서는 sample들로 하기에 action value ft값인 expectation을 계산할 수 없습니다. 따라서 MC policy evaluation에서는 empirical mean return을 사용합니다. sample로 return값들을 얻을 텐데 이를 평균내어 사용하게 됩니다.
First/Every visit : (s,a) pair 에서 각각 나온 return값들을 하나만 사용할지 다 사용할지.
increment count : state action pair가 몇 번 나왔는지 count
increment total sum : return값들을 누적
=> 평균을 구하기 위해 Q(s,a)=S(s,a)/n(s,a)로 Q value estimate를 구해줍니다.
만약 return값들이 iid를 만족하고 에피소드를 계속 늘려서 n(s,a)->무한대 로 보내면 큰수의 법칙에 의해 Q value estimate는 true Q값으로 converge하게 됩니다.
위를 계산하기 위해 increment count, increment total sum을 항상 기록해두어야 합니다.
이것을 개선하여 incremental mean을 사용합니다.
k까지의 평균을 구한다고 하면, k-1까지의 평균에 현재 값만 알면 쉽게 구할 수 있게 됩니다. 또 다른 변수가 필요 없게 됩니다. 계속 incremental하게 update만 하면 됩니다.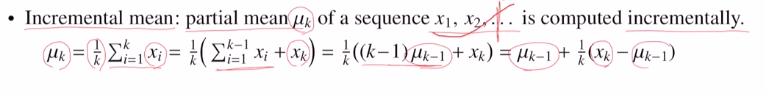
이를 이용하여 incremental monte carlo update를 진행합니다.
여기서 1/n(St,At) 의 값은 0에 가까워지며 줄어들게 됩니다. 하지만 이는 손해입니다. 왜냐하면 뒤에 붙어있는 현재 값의 영향이 작아지기 때문입니다.
따라서 이것을 개선하고자 step size를 설정하여 알파라는 상수로 대체합니다.
이렇게 되면 최근 값도 일정 비율로 참여한다는 장점이 있게 됩니다.
non-stationary problem이 됩니다. agent가 시간이 점점 지날 수록 성능 즉 policy가 좋아집니다. reward prob가 바뀔 수 있다는 것 입니다. non iid 입니다. 특히 동전을 계속 같은 곳에서 던져야 하는데 agent가 점점 성능이 좋아지는 agent이기에 항등분포를 만족하지 않습니다. 따라서 알파를 사용하는 것이 효율적입니다.
또한 알파를 사용하면 바로 전에 나왔던 Q value estimate에 곱해주는 것입니다.
이렇게 함으로 old 에피소드를 exponential하게 감소시키는 역할을 합니다.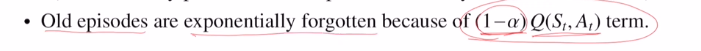
고려대학교 오승상 교수님 강화학습 강의 : https://www.youtube.com/watch?v=eibrMjPEAMg&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=11
