이번 포스터에서는 Implicit Quantile Network: IQN을 알아보겠습니다!
우선 Distributional Reinforcement learing을 상기시켜 보겠습니다.
이것의 핵심은 reward의 randomness에 초점을 맞춘 것 입니다.
reward를 random variable로 보기로 했습니다.
이 reward를 확률분포로 생각하기 때문에 이것의 discounted sum인 return도 확률분포이기에 이것을 action value distribution이라고 했습니다. 이것의 expectation을 구하면 그것은 Q ft이 됩니다.
중요한 것은 Q ft보다는 action value distribution을 본다고 했습니다.
그렇기에 더이상 bellman eq를 사용하지 않고, 분포 사이를 정의한 Distributional bellman eq를 사용합니다.
그런데 가장 중요한 점은 policy가 주어졌을 때 Distributional bellman operator가 contraction이 된다는 점이었습니다. Q ft을 다룰 때는 실수값의 차이만 따지면 되었지만, 이제는 분포 사이를 따지기에 여기서는 Wasserstein metric을 사용했습니다. 그 이유는 이 metric을 사용했을 때만 contraction이 가능했기 때문입니다.
contraction이 된다는 것은 bellman update를 통해 학습을 하게 될 텐데, 각 iteration이 converge한다는 것이고 최종적으로 optimal target distribution을 찾게 됩니다.
이렇게 이론적으로는 훌륭하지만 practical 하게 사용하기는 어렵습니다.
그 이유로는 Wasserstein metric을 implementation하기에는 상당히 어렵습니다. 미분이 불가하여 SGD를 할 수 없기 때문입니다. 또한 기존의 DQN모델을 본다고 할 때 DQN은 input으로 state이 들어오면 output으로 각 action에 대한 Q value 값인 action의 개수만큼 실수값을 출력했습니다. 하지만 이제는 Q ft이 아닌 분포를 사용하기에 network가 distribution을 출력해야 하는데 이것은 불가능합니다. 이 두 가지 문제가 있었습니다.
따라서 이를 해결하기 위해 approximation해서 사용했습니다.
discrete하게 분포를 쪼개어 사용했는데 이것을 통한 방법이 C51, QR-DQN, IQN입니다.
DQN은 input으로 state x가 들어오고, 출력으로 각 action에 대한 Q 값을 출력했습니다.
(action의 개수만큼 출력)
C51에서는 각 action에 대해서 정확하게는 action value distribution을 출력해야 하지만, 이것이 불가능하기에 fixed support로 discrete하게 바꾸어 approximate하여 출력하였습니다.
pi를 학습 가능한 파라미터로 잡고 학습을 진행하였습니다.
(action 개수 x support 개수)
QR-DQN은 각각의 확률을 일정하게 1/N으로 통일하고, 이번에는 이전의 fixed return값들을 learnable로 바꾸어 줍니다. CDF의 inverse값을 학습하는 것이 목표였습니다.
(action 개수 x support 개수)
학습해야 할 return값들은 quantile midpoints에 대해 CDF의 inverse를 학습하는 것이었습니다. 여기서 loss ft은 quantile regression을 사용하였는데 이것을 최소화하는 것이 Wasserstein metric을 최소화하는 것과 같았습니다. 또한 미분이 가능하기에 SGD를 사용하여 학습을 할 수 있었습니다.
이번 포스터에서 알아볼 IQN은 implicit입니다. QR-DQN은 explicit으로 목표로 하는 target 분포가 일치했습니다. 하지만 IQN은 quantile midpoint가 아닌 random하게 샘플링하여 그에 맞는 return값을 찾아갑니다. 그것을 통해 Z를 유추하게 됩니다. 이렇게 샘플링을 사용하기에 implicit이라고 표현합니다.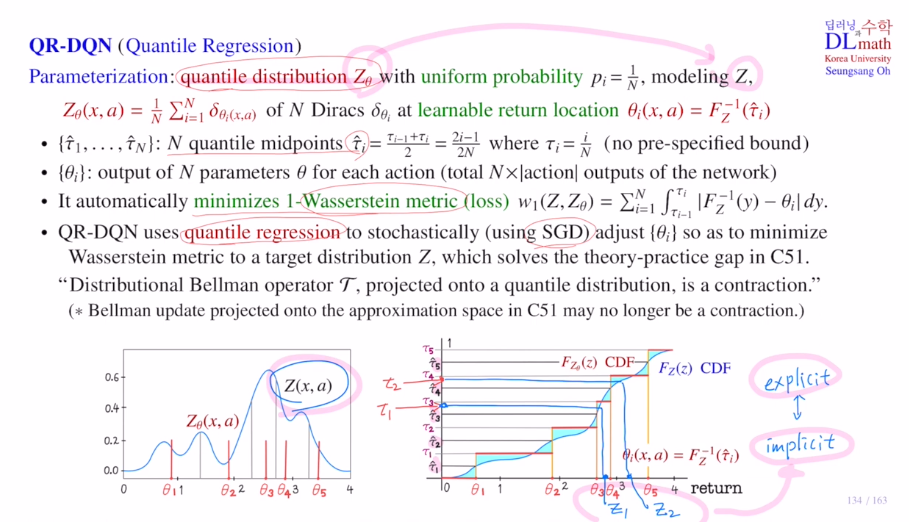
IQN은 Z라는 target distribution이 있을 때, 이것을 approximate하는데 사용되는 quantile value들을 기존 QR-DQN에서는 N개의 quantile midpoints를 사용했다면, 이제는 그렇지 않고 U[0,1]에서 uniform하게 random sampling을 하여 타우들을 뽑고, 그것을 기준으로 CDF의 inverse의 image를 통해 사용하게 됩니다. 샘플을 가지고 표현하기에 implicit하게 표현된다고 합니다.
여기서의 장점은 더이상 return개수가 fixed가 아닌, random sampling을 하기에 원하는 만큼 뽑아 자유롭게 사용할 수 있다는 장점이 있습니다. 이전에는 point를 많이 뽑으면 approximate 에러가 줄어들기에 quantile midpoint의 개수에 depend했지만, IQN은 random sampling을 하기에 approximate 에러가 quantile의 숫자에 영향을 받지 않습니다. network의 사이즈나 학습해야 할 데이터 양에 depend하게 됩니다.
또한 IQN의 추가적인 장점은 risk-sensitive policies를 적용할 수 있다는 점입니다. 여러가지의 distortion risk measures를 사용합니다. 다양한 distortion risk measures를 통해 여러가지 risk-sensitive policies를 적용할 수 있다는 것 입니다.(policy에만 적용가능합니다.)
distortion risk measures β는 [0,1]->[0,1] uniform distribution에서 또 다른 uniform distribution으로 보내주는 것 인데, 예를 들어 quantile value들을 U[0,1]에서 샘플링하였는데 이 값들을 약간씩 아래로 보내게 하여 return값들이 작은 쪽으로 움직이게 하는 것 입니다. 이렇게 하여 policy를 조절할 수 있게 됩니다.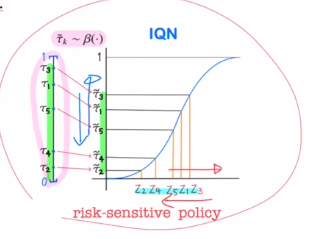
Risk-Sensitive Reinforcement Learning
기존의 greedy policy는 Q값을 maximize하는 action을 선택하는 것 이었습니다.
risk-sensitive policy는 추가적인 term이 붙어 그 식을 maximize하는 action을 선택하는 것 입니다.
아래 pdf를 보면 a1은 variance가 적어 loew risk를 나타냅니다. a1은 평균적으로 8을 얻고 낮으면 7 높으면 10정도를 얻습니다.
a2는 반대로 variance가 높아 risk가 큽니다. 평균적으로 10을 얻지만 낮으면 5를 얻게 됩니다.
안전한 것을 원하는 사람은 a1을 선택하게 될 것 입니다.
하지만 만약 기존의 greedy policy를 사용하게 된다면 평균값이 높은 a2를 선택하게 됩니다.
따라서 risk-averse 를 추가하기 위해 뒤의 term을 추가한 것 입니다.
β를 양수로 주는 것인데 β=2라고 할 때, [m-2σ, m+2σ]<-95% 이기에 2.5%정도 평균에서 빼주어기준선을 이동시킵니다. variance가 더 큰 것은 많이 움직이게 됩니다.
이렇게 되면 a1을 선택하게 변경됩니다.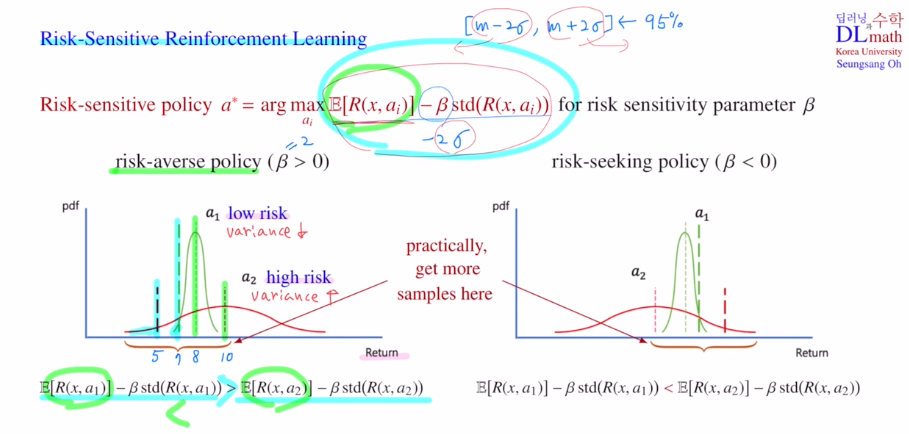
이번에는 risk-seeking policy를 보겠습니다.
오른쪽 그림을 보면 a1을 선택하게 될 것 입니다. 하지만 평균값이 떨어지더라도 높은 값을 얻을 수 있는 a2를 선호하는 사람이 있을 수도 있습니다. 이 때는 β를 음수로 둡니다. variance가 더 큰 것은 많이 움직이게 됩니다. 그렇기에 a2를 선택하게 됩니다.
β를 risk sensitivity parameter라고 하는데 이 베타값을 조절하여 risk를 얼마나 줄지 정합니다.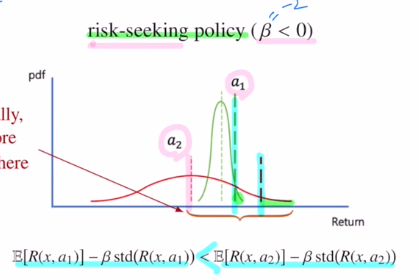
하지만! Risk-Sensitive Reinforcement Learning에서는 베타값을 실제 계산하지 않고 앞 expectation만 계산하게 됩니다. 이제는 expectation자체를 샘플링을 통해 움직입니다.
만약 low risk를 원하면 왼쪽에서 더 많은 샘플을 뽑는 것 입니다. 이렇게 베타와 동일한 효과를 내도록 합니다.
그렇다면 균등하지 않게 샘플링은 어떻게 할까요?
-> distortion risk measure을 사용합니다.
Changing sample distribution
distortion risk measure은 [0,1]->[0,1]로 보내는 함수인데 전체적으로 밑으로 내리거나 올리는 역할을 합니다. policy에서만 적용됩니다. maximize하는 action을 찾을 때만 사용된다는 것 입니다.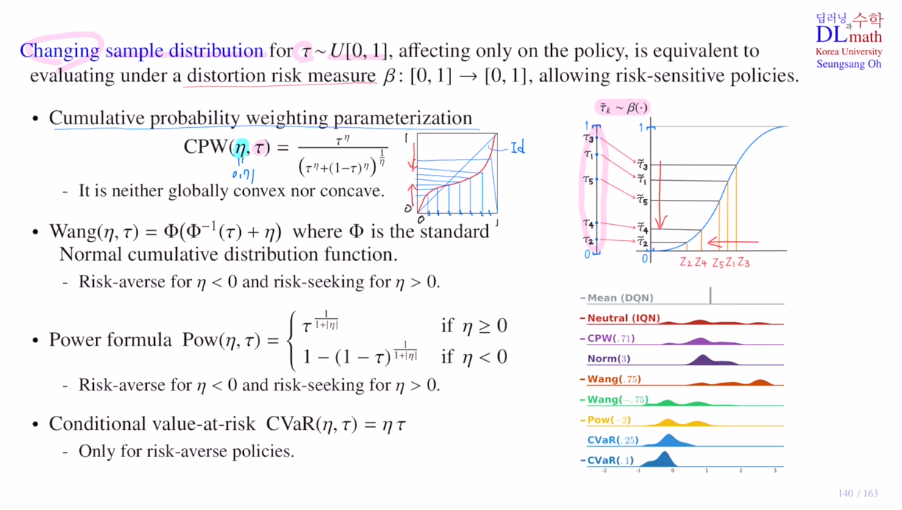
distortion risk measure의 종류가 있는데 이를 소개하겠습니다.
1) Cumulative probability weighting parameterization: CPW
공식을 통해 변형시킵니다.
에타값이 1이면 아무것도 바뀌지 않은 상태이고 작아질 수록 휘어져서 나옵니다.
global하게 convex or concave가 아닌 일부분은 convex, 일부분은 concave로 작은 값은 키워주고 높은 값은 작게 해줍니다. 가운데로 모아주게 됩니다.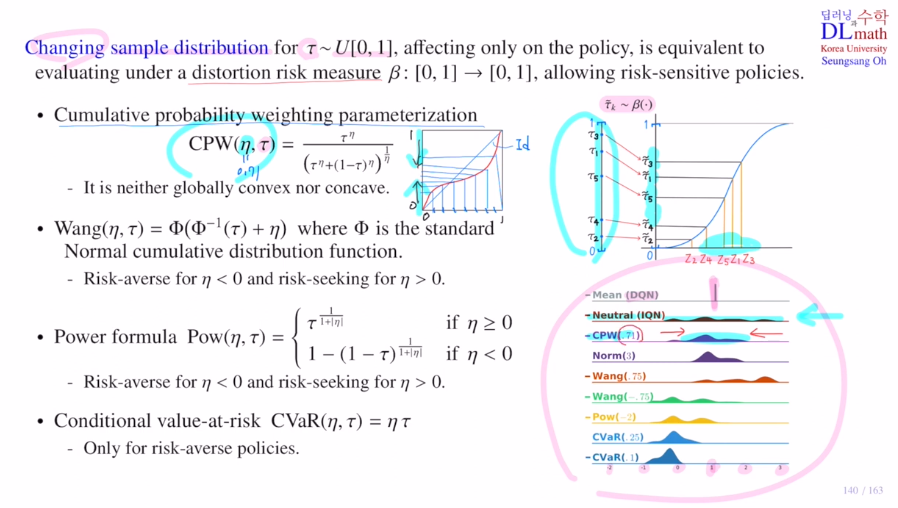
2) Wang
Φ는 표준정규분포의 CDF입니다.
타우값을 CDF의 inverse로 보내서(어떤 z값이 나오고) 에타만큼 더한 후(에타값이 양수면 오른쪽으로 이동) CDF로 보낸 것(기존 타우값보다 위로 상승) 입니다.
이렇게 에타값이 음수면 아래로 양수면 위로 옮겨주는 효과가 있습니다.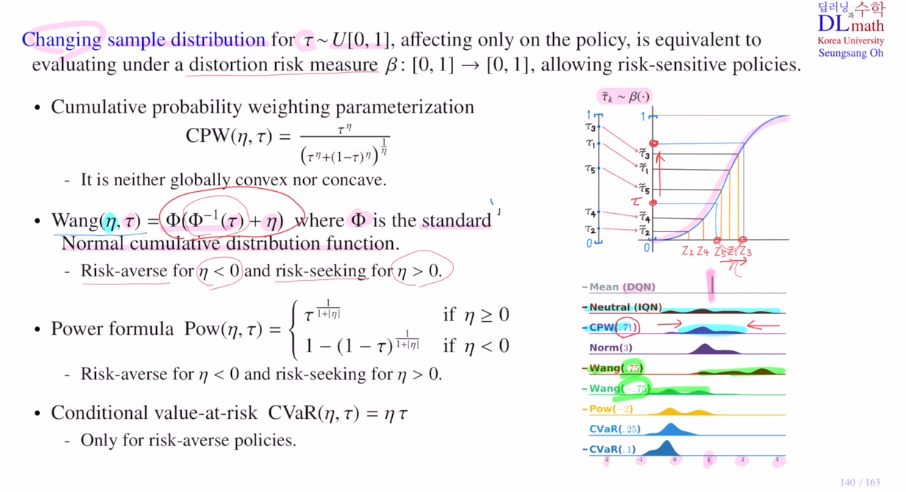
3) Power formular
에타값이 0보다 크면 concave ft을 적용하여 risk seeking으로 타우 값을 올려주고, 0보다 작으면 risk averse로 타우 값을 내려주게 됩니다.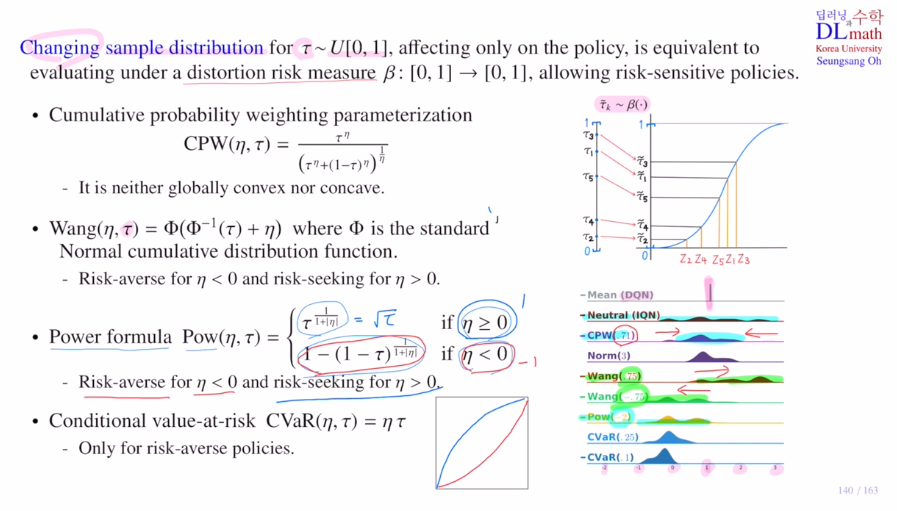
4) Conditional value-at-risk: CVaR
그냥 linear하게 에타를 곱해주는 것 입니다. 에타값을 0.5로 하면 전체적으로 내려주기에 only risk averse policy에 해당됩니다.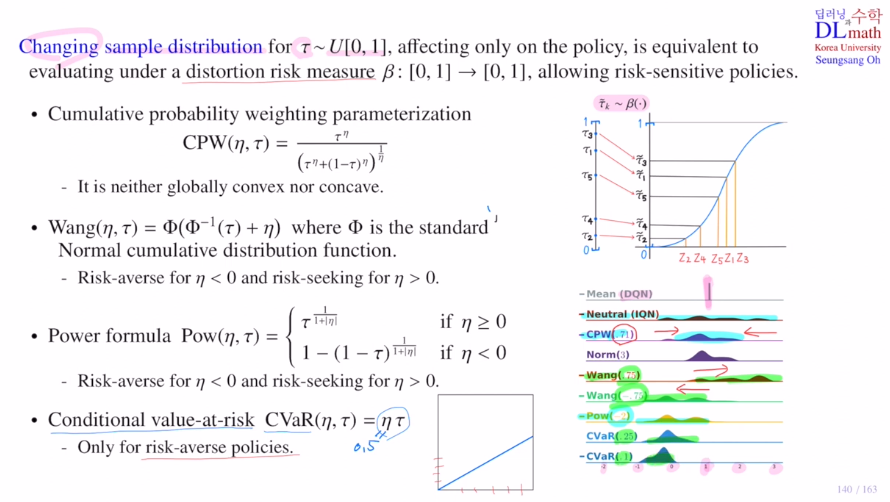
이러한 방법들로 risk seeking을 할지, risk averse를 할지 정해주는 것 입니다!
마지막으로 실제 implementaiton을 알아보겠습니다.
IQN network는 quantile ft을 approximate하는 것 입니다.
이것은 Uniform distribution에서 타우를 qunatile value 로 하나 선택한 다음에 target distribution의 CDF의 inverse값에 해당하는 return값을 학습하는 것 입니다.
이 과정에서 risk-sensitivity policy를 적용하는 것 입니다.
policy를 정할 때 적용을 합니다. 다시 말해 greedy policy a* 를 정할 때 사용하는데, Q값을 maximize하는 action을 선택합니다. 여기서는 Q value값이 약간 변형되어 distorted expectation이라고 하겠습니다. uniform distribution에서 qunatile value 타우를 선택하고 원래는 바로 적용해서 Z타우(x,a)를 만드는데, 이제는 distorted expectation을 사용합니다.
IQN모델을 보면 추가된 부분이 있습니다. 이제는 state만 input으로 들어오는 것이 아닌 quantile value도 input으로 들어오게 됩니다. output은 모든 quantile midpoints에서 값을 출력하는 것이 아닌 quantile 값에 해당하는 하나의 값만 출력합니다. 각 action별로 하나씩만 출력하게 됩니다. 최종 action의 개수만큼 출력합니다.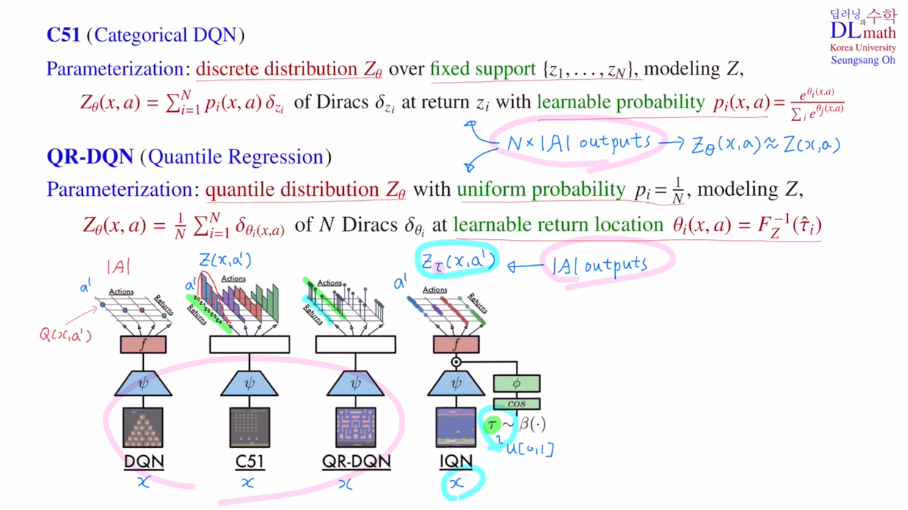
네트워크로 approximate하는 것을 살펴보겠습니다.
아래는 기존의 DQN 네트워크 입니다.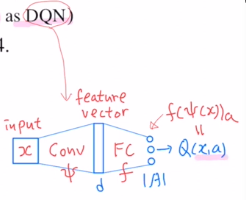
IQN은 새로운 quantile value τ가 있습니다.
이 quantile value τ를 dimension이 d인 feature vector로 만들어줍니다.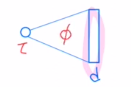
이제 두 정보를 합쳐서 f라는 FC layer로 보냅니다.
합치는 방법은 element multiple이 있고, 둘을 concat할 수도 있습니다.
혹은 residual 효과를 내게 할 수도 있습니다.
이를 통해 궁극적으로 Zτ(x,a)를 출력하게 됩니다.
본 논문에서는 τ를 n(=64)개의 약간 변형된 copy를 한 후 FC를 사용하고 Relu를 통해 dim d인 feature vector를 만들게 됩니다.
τ는 greedy policy를 정할 때 나오고, target network에서 한 번 나오고, behavior network에서 한 번 나옵니다. IQN에서는 샘플의 개수가 고정되어 있지 않기에 세 번 다 다르게 샘플링을 진행합니다. N,N',K
distortion risk measure은 greedy policy를 정할 때만 사용됩니다.
이것은 아주 중요한 이유가 있는데 action value distribution인 Z(x,a) 자체를 변형시키지는 않습니다. 이것 자체는 가지고 있고, 이것을 통해 policy를 정할 때만 distortion시키는 것 입니다.
하이퍼파라미터를 정하고, distortion risk measure 베타를 정합니다.
-> transition을 가져와 distortion risk measure를 통해 약간 변형시켜 가져옵니다.
-> distorted되어 있는 Q ft을 계산합니다.
-> 이것을 maximize하는 action을 선택해서 greedy policy로 선택합니다.
-> uniform distribution에서 quantile value를 선택하는데 behavior network에 있는 값을 결정하기 위해 선택하는 것이고, 아래에서 선택하는 quantile value들은 target network을 위해 선택한 것 입니다.
-> 이 target, behavior의 출력값을 가지고 TD error를 가능한 샘플 페어별로 계산합니다.
-> TD error를 Quantile Huber loss로 계산합니다. 각 페어들마다 찾은 다음에 결정하고 minimize하는 방향으로 학습합니다.
고려대학교 오승상 교수님 강화학습 강의 : https://www.youtube.com/watch?v=RihBHbp9dBA&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=34
