핸즈온 머신러닝 - Part1. 머신러닝 ch8. 차원 축소(3) 다른 차원 축소 기법

앞에서 설명드린 차원 축소 기법 이외에도 다양한 기법들이 존재합니다.

1) MDS : Multi-Dimensional Scaling
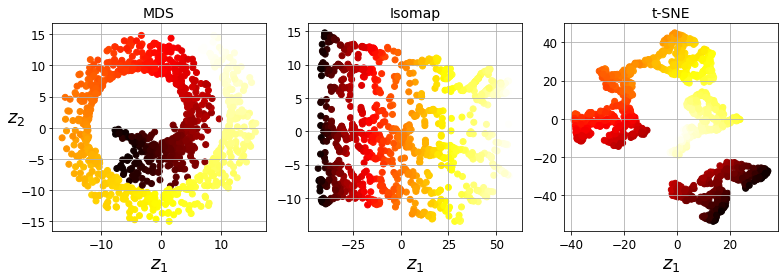
샘플 데이터들 간의 거리를 보존하면서 차원을 축소하는 기법입니다.

2) Isomap
각 데이터 포인트를 가장 가까운 이웃과 연결하는 식의 그래프를 만든 후 그래프에서 두 노드 사이의 최단 경로를 이루는 노드의 수인 geodesic distance를 유지 하면서 차원을 축소합니다.

3) t-SNE : t-distributed Stochastic Neighbor Embedding
비슷한 데이터는 가까이, 비슷하지 않은 데이터는 멀리 떨어지게 차원을 축소합니다. 주로 시각화에 많이 사용되며, 특히 고차원 공간에 있는 데이터의 군집을 시각화할 때 사용합니다.

4) LDA : linear discriminant analysis
LDA의 목적은 데이터들을 특정 한 축에 projection한 후에 각 범주들을 잘 구분할 수 있는 직선을 찾는 것을 목표로 합니다. 즉, 사영 후 범주들의 평균이 서로 멀어지고, 각 분산이 작도록 하는 것을 목표로 잡습니다.

아래는 스위스 롤에 위 알고리즘을 적용한 코드입니다.

# 스위스 롤
from sklearn.datasets import make_swiss_roll
X, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=41)


# 1) MDS
from sklearn.manifold import MDS

mds = MDS(n_components=2, random_state=42)
X_reduced_mds = mds.fit_transform(X)

# 2) Isomap
from sklearn.manifold import Isomap

isomap = Isomap(n_components=2)
X_reduced_isomap = isomap.fit_transform(X)

# 3) t-SNE
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, random_state=42)
X_reduced_tsne = tsne.fit_transform(X)

# 4) LDA
from sklearn.discriminant_analysis import LinearDiscriminantsAnalysis

lda = LinearDiscriminantsAnalysis(n_components=2)
X_mnist = mnist['data']
y_mnist = mnist['target']
lda.fit(X_mnist, y_mnist)
X_reduced_lda = lda.transform(X_mnist)