동적계획법

동적계획법이란?

문제를 여러 개의 간단한 문제로 분리하여 부분의 문제들을 해결함으로써 최종적으로 복잡한 문제의 답을 구하는 방법이다.

원리 및 구현방식

1. 큰 문제를 작은 문제로 나눌 수 있어야 한다.
2. 작은 문제들이 반복돼 나타나고 사용되며 이 작은 문제들의 결괏값은 항상 같아야한다.
3. 모든 작은 문제들은 한 번만 계산해 DP 테이블에 저장하며 추후 재사용할 때는 이 DP 테이블을 이용한다.
4. 동적 계획법은 톱-다운, 바텀-업 방식으로 구현할 수 있다.

예시

피보나치 수열

피보나치 수열 공식

D[N] = D[N-1] + D[N+2]

1. 동적 계획법으로 풀 수 있는지 확인하기

• 피보나치 수열은 위 공식 처럼 작은 문제로 나눌 수 있기 때문에 DP로 풀 수 있다.

2. 점화식 세우기

• 다양한 문제를 만났을 때 이들의 인과관계를 파악하는 것이 중요하다.
• 피보나치 수열의 경우 알고 있는 공식을 그대로 사용하면 된다.

3. DP 테이블 사용 이해하기

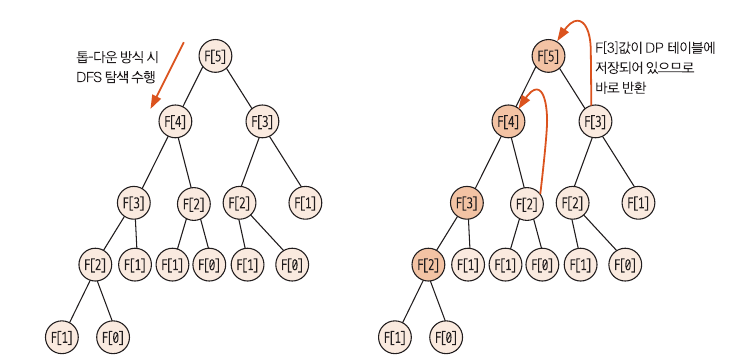
4. 톱다운 구현 방식

• 톱다운 구현방식은 말 그대로 위에서부터 내려가기 때문에 보통 재귀함수로 많이 구현된다.

5. 바텀 업 구현 방식

• 바텀없 구현방식은 밑에서 부터 올라가며 값을 찾아나가기 때문에 보통 반복문으로 많이 구현된다.

예제

예제를 풀며 두가지 방식 모두 구현해보자.
백준 정수 1로 만들기

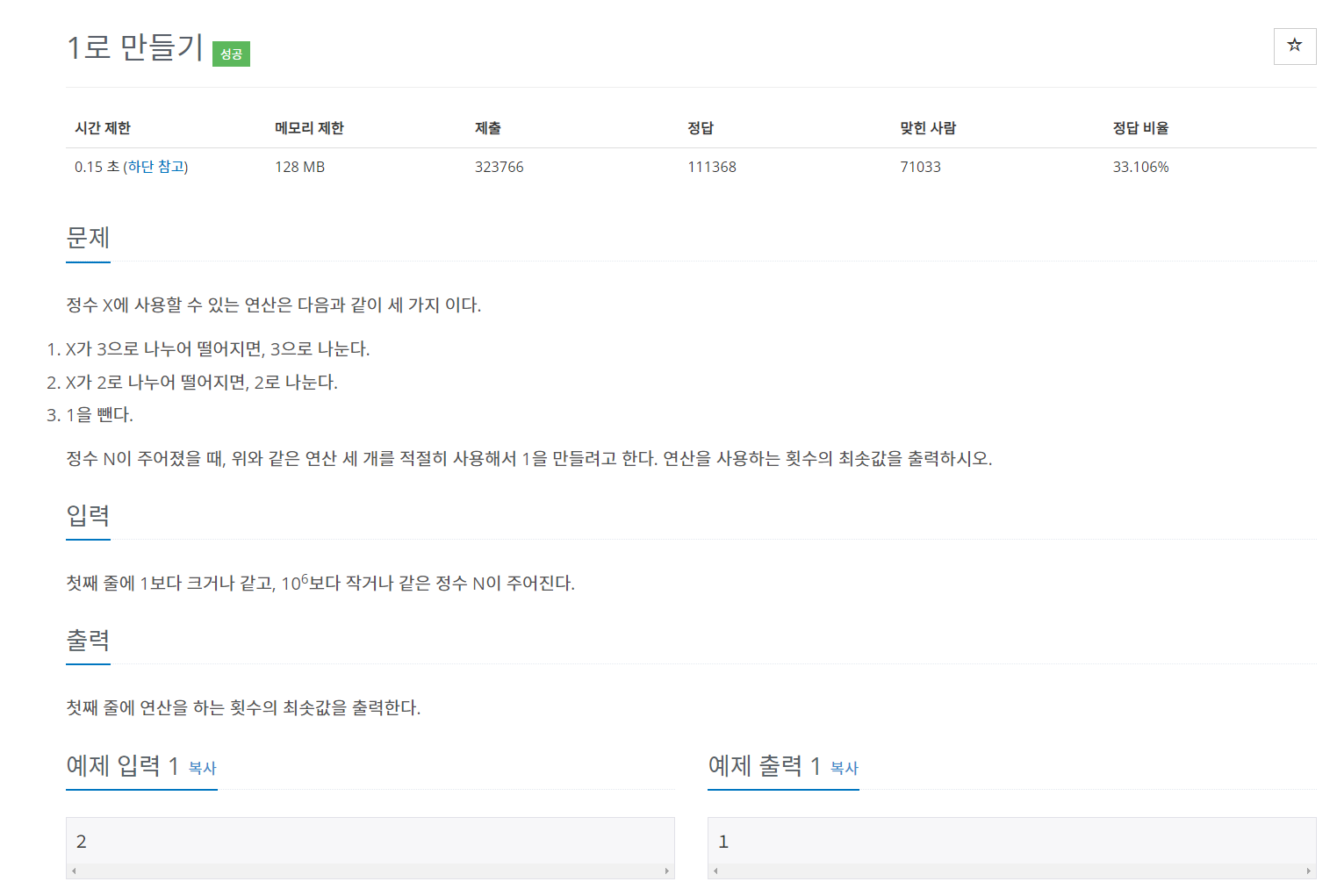
톱다운 방식

N에서 부터 1까지 내려가면서 값을 찾는 방식으로 접근하였다. 재귀함수 방식을 사용했다.

#include <iostream>

using namespace std;

int a[1000001] = {0,0,1,1};

int func(int N) {
	int x;
	if (N == 1 || N == 0) return 0;
	else if (a[N] != 0) return a[N];
	else if (N > 3) {
		x = 1 + func(N - 1);
		if (N % 3 == 0) x = min(x, a[N / 3] + 1);
		if (N % 2 == 0) x = min(x, a[N / 2] + 1);
		a[N] = x;
		return x;
	}
}
int main() {
	int N = 0;
	cin >> N;
	cout << func(N);
}

바텀업 방식

1에서부터 N으로 올라가면서 값을 찾는 방식으로 접근하였다. 해당 문제의 경우 이 방식이 훨씬 빠르게 탐색이 가능하다.
재귀함수 특성상 그냥 왠만하면 반복문을 사용하는 방식이 빠르긴 하다.

#include <iostream>
#include <vector>

using namespace std;

int main()
{
	int n;
	cin >> n;

	vector<int> vec(n + 1, 1e9);
	vec[0] = 0;
	vec[1] = 0;
	
	for (int i = 1; i <= n; ++i)
	{
		if (i + 1 <= n)
		{
			if (vec[i] + 1 < vec[i + 1])
			{
				vec[i + 1] = vec[i] + 1;
			}
		}

		if (i * 2 <= n)
		{
			if (vec[i] + 1 < vec[i * 2])
			{
				vec[i * 2] = vec[i] + 1;
			}
		}

		if (i * 3 <= n)
		{
			if (vec[i] + 1 < vec[i * 3])
			{
				vec[i * 3] = vec[i] + 1;
			}
		}
	}

	cout << vec[n];
}

위가 바텀업이고 아래가 톱다운 방식이다.
확실히 재귀함수 때문에 메모리를 많이 먹는 것을 볼 수 있었다.