조합

핵심이론

조합

조합은 n개의 숫자에서 r개를 뽑는 경우의 수를 뜻한다.

공식

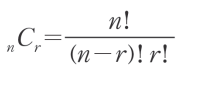
순열

순열은 n개의 숫자 중 r개를 뽑아 순서를 고려해 나열할 경우의 수를 이야기 한다.

공식

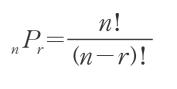
문제 접근 방법

ex) 5개의 데이터에서 3개를 선택하는 조합의 경우의 수를 구하여라

1. 모든 부분 문제가 해결된 상황을 가정해보자

위 문제의 경우 5개 중 4개의 데이터의 선택 여부가 결정되었다고 생각해보자.

그럼 5개 중에 3개를 선택하는 경우의 수는 마지막 데이터를 선택하느냐의 여부에 따라 두 가지로 나뉜다.

1. 마지막 데이터를 선택하지 않았을때
   -> 앞 4개의 데이터 중 3개를 선택하는 경우의 수

2. 마지막 데이터를 선택했을 때
   -> 앞 4개의 데이터 중 2개를 선택하는 경우의 수

1의 경우의 수와 2의 경우의 수를 합치면 이 문제의 답이 도출된다.
이를 점화식 D[5][3] = D[4][2] + D[4][3]으로 표현할 수 있다.

2. 가정한 내용을 바탕으로 일반식을 도출한다.

위의 점화식을 바탕으로 일반 조합 점화식을 한번 도출해보면
D[i][j] = D[i-1][j] + D[i-1][j]로 표현할 수 있다.

연습문제

백준 11051 이항계수 2

코드

#include <iostream>
#include <vector>

using namespace std;

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);

	int n, k;
	cin >> n >> k;

	vector<vector<long>> D(n + 1, vector<long>(n + 1, -1));

	for (int i = 0; i <= n; i++)
	{
		D[i][1] = i;
		D[i][i] = 1;
		D[i][0] = 1;
	}

	for (int i = 2; i <= n; i++)
	{
		for (int j = 1; j < i; j++)
		{
			if (D[i][j] = -1)
			{
				D[i][j] = D[i - 1][j - 1] + D[i - 1][j];
				D[i][j] = D[i][j] % 10007;
			}
		}
	}

	cout << D[n][k];
}

회고 및 느낀점

모듈러 연산의 특성을 잘 몰라서 굉장히 헤맸던 문제이다.
처음에 무식하게 진짜 이항계수를 구해서 %10007만 하면 되는 줄 알았으나 값의 범위가 long타입을 아득히 벗어나기 때문에 다른 방법을 사용해야했다.

모듈러 연산의 특징 (A%n + B%n) % n = (A+B) % n
을 활용하여 점화식으로 풀이하게 된다면
D[i][j]는 D[i-1][j] + D[i-1][j]으로 표현될 수 있으므로
D[i][j]%n을 구할 때 D[i-1][j]%n + D[i-1][j]%n을 구해도 상관없으므로 식을 세울 수 있다.

이런 특성을 잘 모른다면 식을 세울 방법조차 찾기 힘드니 이런 배경 지식은 참 중요하다는 생각이 들었다.. 열심히 공부해야지