벨만-포드

벨만포드 알고리즘은 그래프에서 최단 거리를 구하는 알고리즘으로, 주요 특징은 다음과 같다.

기능

특정 출발 노드에서 다른 모든 노드까지의 최단 경로 탐색

특징

음수 가중치 에지가 있어도 수행할 수 있다.
전체 그래프에서 음수 사이클의 존재 여부를 판단할 수 있다.

시간복잡도

O(VE)

구현 방법

1. 에지 리스트로 그래프를 구현하고 최단 경로 배열 초기화하기

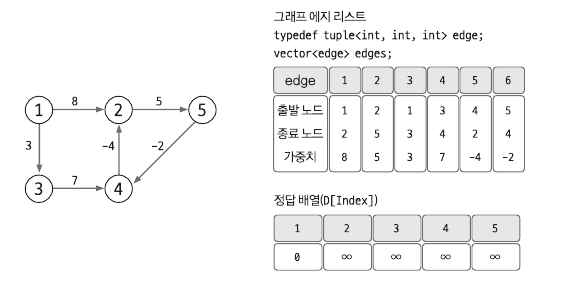
2. 모든 에지를 확인해 정답 배열 업데이트하기

최단 거리 배열에서 업데이트 반복 횟수는 노드 개수-1이다. 노드 개수가 N이고 음수 사이클이 없을 때 특정 두 노드의 최단 거리를 구성할 수 있는 에지의 최대 개수는 N-1이기 때문이다.
에지 E(s,e,w)에서 다음 조건을 만족하면 업데이트를 실행한다.

E(s,e,w) (s=시작노드, e=끝노드, w=가중치)
D[s]!=INF이며 D[e]>D[s]+w일 때 D[e]=D[s]+w로 배열의 값을 업데이트

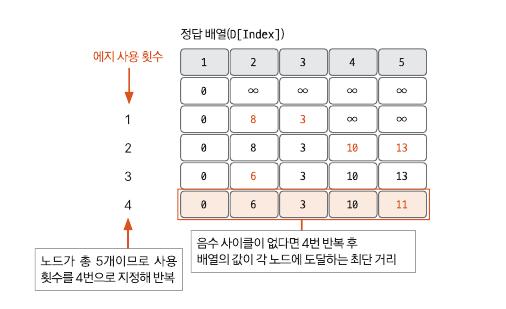
이렇게 음수 사이클이 없을 때 N-1번 에지 사용 횟수를 반복하면 출발 노드와 모든 노드 간의 최단 거리를 알려 주는 정답 배열이 완성된다.

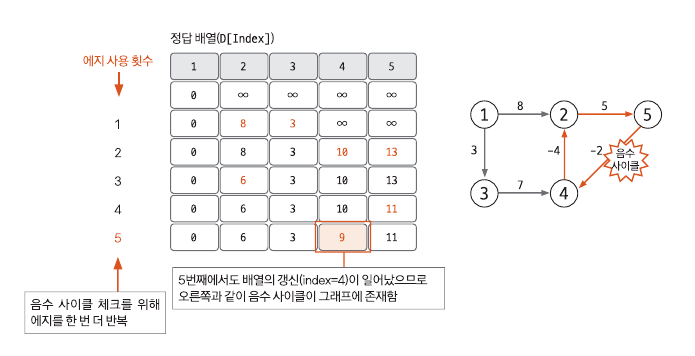
3. 음수 사이클 유무 확인

음수 사이클 유무를 확인하기 위해 모든 에지를 한 번씩 다시 사용해 업데이트 되는 노드가 발생하는지 확인한다. 만약 업데이트되는 노드가 있다면 음수 사이클이 있다는 뜻이며 최단 거리를 찾을 수 없는 그래프라는 뜻이 된다.

연습문제

백준 11657 타임머신

코드

#include <iostream>
#include <vector>

using namespace std;

void bellman_ford();
int checkAndUpdateDist();

struct edge
{
	int s;
	int e;
	int cost;
};

int n, m;
vector<edge> edges, start, end;
vector<long long> dist;

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);

	cin >> n >> m;
	edges.resize(m + 1);
	dist.resize(n + 1, 1e9);
	for (int i = 1; i <= m; i++)
	{
		int s, e, cost;
		cin >> s >> e >> cost;
		edges[i] = { s,e,cost };
	}

	bellman_ford();
	
	if (checkAndUpdateDist())
	{
		cout << "-1";
	}
	else
	{
		for (int i = 2; i <= n; i++)
		{
			if (dist[i] != 1e9)
			{
				cout << dist[i] << '\n';
			}
			else
			{
				cout <<  "-1\n" ;
			}
		}
	}
}

void bellman_ford()
{
	dist[1] = 0;
	for (int i = 1; i < n; i++)
	{
		checkAndUpdateDist();
	}
}

int checkAndUpdateDist()
{
	int flag = 0;
	for (int j = 1; j <= m; j++)
	{
		int s = edges[j].s;
		int e = edges[j].e;
		int cost = edges[j].cost;
		if (dist[s] != 1e9 && dist[s] + cost < dist[e])
		{
			dist[e] = dist[s] + cost;
			flag = 1;
		}
	}
	return flag;
}

어려웠던 점

출력 초과가 뜨는 바람에 대체 어디서 출력 초과가 생기는지 감이 잡히지 않아서 한참을 헤메다가.. 결국 질문 게시판을 보고야 말았는데
dist의 범위가 int를 벗어나는 바람에 문제가 생기는 것이었다.

앞으로 이런 어떤 값을 구하는 문제에서 값의 타입도 신경을 쓰며 해야겠다.