플로이드-워셜

플로이드-워셜 알고리즘은 그래프에서 최단 거리를 구하는 알고리즘이다.

기능

• 모든 노드 간에 최단 경로 탐색

특징

• 음수 가중치 에지가 있어도 수행할 수 있다.
• 동적 계획법의 원리를 이용해 알고리즘에 접근한다.

시간 복잡도

• O(V^3)로 느린 편이라서 노드의 갯수를 잘 보고 사용해야할 알고리즘이다.

핵심이론

A노드에서 B노드까지 최단 경로를 구했을 때, 최단 경로 위의 K노드에서 B노드로 향하는 부분 경로 역시 최단 경로이다.

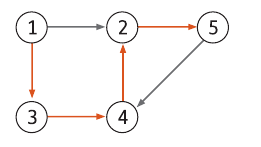
1->5의 최단 경로에서 1->4, 4->5의 최단 경로는 1->5의 최단 경로를 따른다.

점화식

D[S][E] = min(D[S][E],D[S][K] + D[K][E])
원래 저장되어 있던 S->E보다 K라는 노드를 거쳐가는 최단 거리가 더 빠른지 비교 후 빠른 쪽을 저장한다.

구현방법

1. 배열을 선언하고 초기화

최단거리 이차원 배열 D를 선언하고 초기화 한다. (D[출발][도착] 인데 보통 출발지 도착지 크기는 노드 갯수로 똑같기 때문에 D[노드갯수][[노드갯수]로 만든다.)
이 때, 출발과 도착지점이 같은 경우에는 0을 초기화하고 나머지는 무한대로 초기화한다.

2. 최단 거리 배열에 그래프 데이터 저장

엣지 데이터 S E Cost를 받는다.
Cost가 D[S][E]보다 작은 경우,
D[S][E] = Cost로 저장한다.

3. 점화식으로 배열 업데이트

점화식을 사용해서 최단 거리의 값을 업데이트 한다.
로직은 다음과 같다 (그냥 완전 탐색)

for 경유지
	for 출발 노드
    	for 도착 노드
        	D[S][E] = min(D[S][E],D[S][K] + D[K][E])

연습문제

백준 11404 플로이드

#include <iostream>
#include <vector>

using namespace std;

struct edge
{
	int s;
	int e;
	int cost;
};

int n, m;
vector<edge> edges, start, end;
vector<vector<long long>> dist;

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);

	cin >> n >> m;

	dist = vector<vector<long long>>(n + 1, vector<long long>(n + 1, 1e9));

	for (int i = 1; i <= n; i++)
	{
		dist[i][i] = 0;
	}

	for (int i = 0; i < m; i++)
	{
		int s, e, cost;
		cin >> s >> e >> cost;
		if (dist[s][e] > cost)
		{
			dist[s][e] = cost;
		}
	}

	for (int k = 1; k <= n; k++)
	{
		for (int s = 1; s <= n; s++)
		{
			for (int e = 1; e <= n; e++)
			{
				dist[s][e] = min(dist[s][e], dist[s][k] + dist[k][e]);
			}
		}
	}

	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			long long d = dist[i][j];
			if (d != 1e9)
			{
				cout << d << ' ';
			}
			else
			{
				cout << '0' << ' ';
			}
		}
		cout << '\n';
	}
}

회고

나름 단순한 알고리즘이어서 그런지 코드 작성 중 막히는 부분은 없었는데 이상하게 첫 시도에 실패하였다.

코드를 자세히 살펴보니 처음 엣지의 데이터를 최소 거리 배열에 넣어줄 때 if문을 빼먹은 채로 넣은 것 때문에 최소 거리 배열에 들어간 값이 최소가 아니라 그냥 가장 최신 값이 들어갔던 것이었다.

간단한 알고리즘이더라도 너무 급하게 하다가 실수하는 일이 없도록 해야겠다..