[프로그래머스] N으로 표현

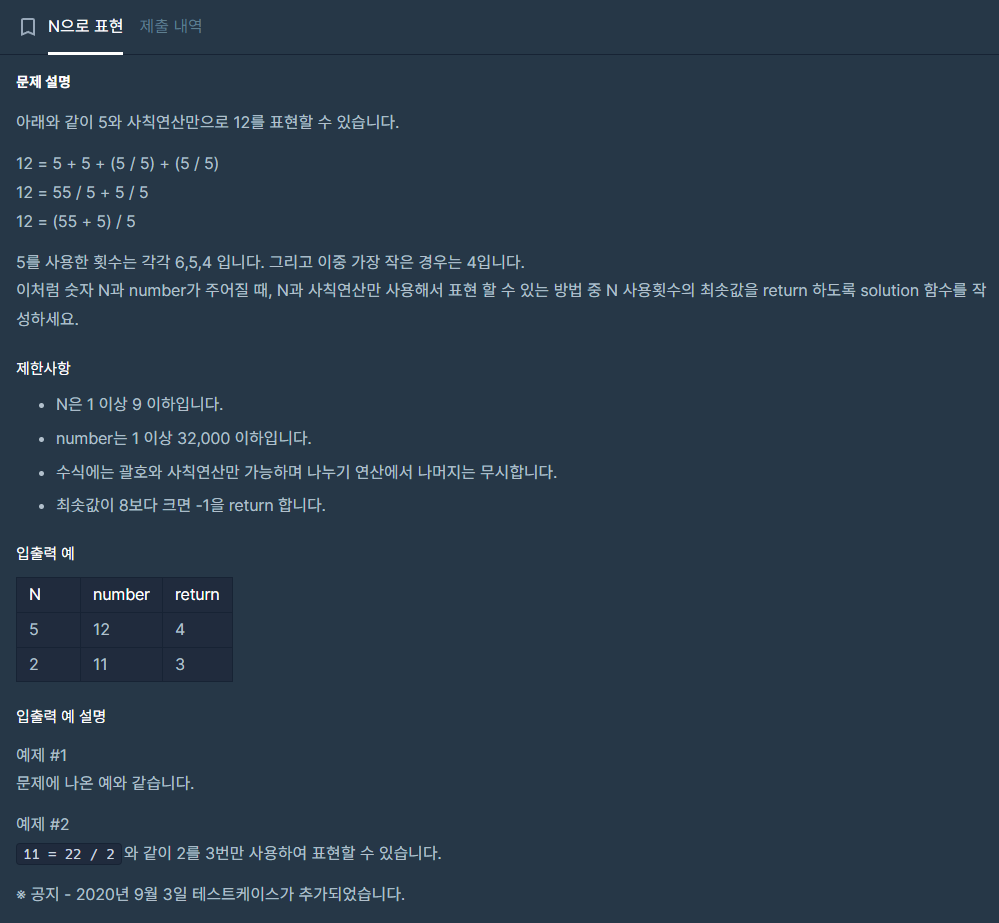
접근 방식에 문제가 있어서 결국 문제를 풀지 못하고 다른 사람의 풀이를 참고했던 문제이다..

접근했던 방식

일단은 다이나믹 프로그래밍 방식을 떠올렸다. 문제는 그 방식이 살짝 잘못됐었다.
D[i]를 자연수 i를 만드는 최소 N의 갯수로 둬버렸던 것이다.
그렇게 해서 만들었던 점화식이
D[i] = min(D[i+N] +1, D[i-N] +1, D[i*N] +1, D[i/N] +1, D[i+1] + 2, D[i-1] + 2)
뭐 이런 괴랄한 식을 세워버렸다.
근데 이 방식의 가장 문제점은 이미 구한 D[i]를 다시 갱신할 방법이 없다는 것
예를 들어 N이 5라고 쳤을 때, 12를 만들 때의 수식에는 55가 들어가는데 이를 탐색할 능력이 없다는 것이다.
그래서 D배열에 미리 5, 55, 555, 5555 ... 이들을 초기화 시켜놓고 문제에 접근을 해보았으나..
이 방식으로는 탐색 범위도 상당히 애매모호해지기 때문에 D배열을 얼마나 잡아야할지 감이 잡히지 않았다.
아무튼 이 문제에 적합한 해결 방식이 아니었다.

하지만 나는 D[i]를 자연수 i를 만드는 최소 N의 갯수로 둔 것에 너무 사로잡혀버려서 문제 풀이가 막혀버렸다.
풀이를 보고나서야 최솟값이 8보다 크면 -1을 return 합니다.의 진정한 의미를 깨닫게 되었다.

풀이 방법

D[i]를 N을 i개 조합해서 만들 수 있는 수들의 집합으로 만들면 된다.
그렇다면 D[i] 은 i개 이하의 모든 사칙연산 조합으로 볼 수 있다.
말이 좀 이상한 것 같은데, 쉽게 말해 그냥 모든 경우의 수를 조합하는 것.

예를 들어 D[2]이면 N 3개로 조합할 수 있는 모든 식을 구하면 된다.
이 말은 D[0] D[1]의 사칙연산으로 만들 수 있는 모든 조합 (정확히는 순열, 나누기나 빼기는 순서에 따라 값이 달라지니까), 그리고 N이 3개 있는 수로 나타낼 수 있다.

이 D[i]를 설정하는 법을 몰라서 냅다 몇시간을 버렸다..
결국 DP의 핵심은 무엇을 D[i]로 지정하고 그것을 어떻게 구할 것인가. 인데 사실상 아무것도 하지 못한 것이다.

#include <string>
#include <vector>
#include <unordered_set>

using namespace std;

int solution(int N, int number) {
    vector<unordered_set<int>> d(8);
    for (int i = 0; i < 8; ++i)
    {
    	//N, NN, NNN 형식의 수를 만들어서 추가해줌
        d[i].insert(stoi(string(i + 1, '0' + N))); 
        
        //i이하의 d로 모든 경우의 수를 탐색하여 d[i]에 추가
        for (int j = 0; j < i; ++j)
        {
            for (int op1 : d[j])
            {
                for (int op2 : d[i - j - 1])
                {
                    d[i].insert(op1 + op2);
                    d[i].insert(op1 - op2);
                    d[i].insert(op1 * op2);
                    if (op2 != 0) d[i].insert(op1 / op2);
                }
            }
        }
    }
    //제일 먼저 찾아 낸 것이 최소
    for(int i=0;i<8;i++)
    {
        if(d[i].find(number) != d[i].end()) return i+1;
    }
    //8개 이내에 못찾았으니 -1
    return -1;
}

회고

일단 다이나믹 프로그래밍이라는 방식으로 바로 풀이법이 떠오른 것 까지는 매우 만족스러웠다.
(방식이 틀려 해결은 못했지만 그럼에도 불구하고)

근데 아직 DP로 접근함에 있어 무엇을 저장해야하는 값으로 정해야하는지에 대한 직관력이 부족한 것 같다.
이 문제에서도 8 이상이라면 -1을 반환한다. 라는 꽤나 명시적인 힌트가 있었음에도 불구하고 이를 써먹을 생각을 제대로 하지 못한 것 같아서 아쉽다.

또한 DP로 풀이할 때, 나도 모르게 DP 배열은 어떤 값으로 고정관념이 박혀있었던 것 같다. 예를 들어 어떤 최솟값이라던가, 최댓값이라던가.
이 문제에서는 집합의 배열으로써 문제를 풀게 된다.
사실 하루종일 이 문제를 잡고 있었어도 떠올리지 못했을 수도 있다.

하지만 이렇게 접근 방법을 하나씩 알아간다면 내 인사이트도 언젠가 이런 문제쯤은 바로 꿰뚫어볼 수 있을 정도가 되지 않을까