[프로그래머스] 등굣길

프로그래머스 등굣길

접근 방식

문제를 보고 처음 떠오른 방법은 아래와 같다.

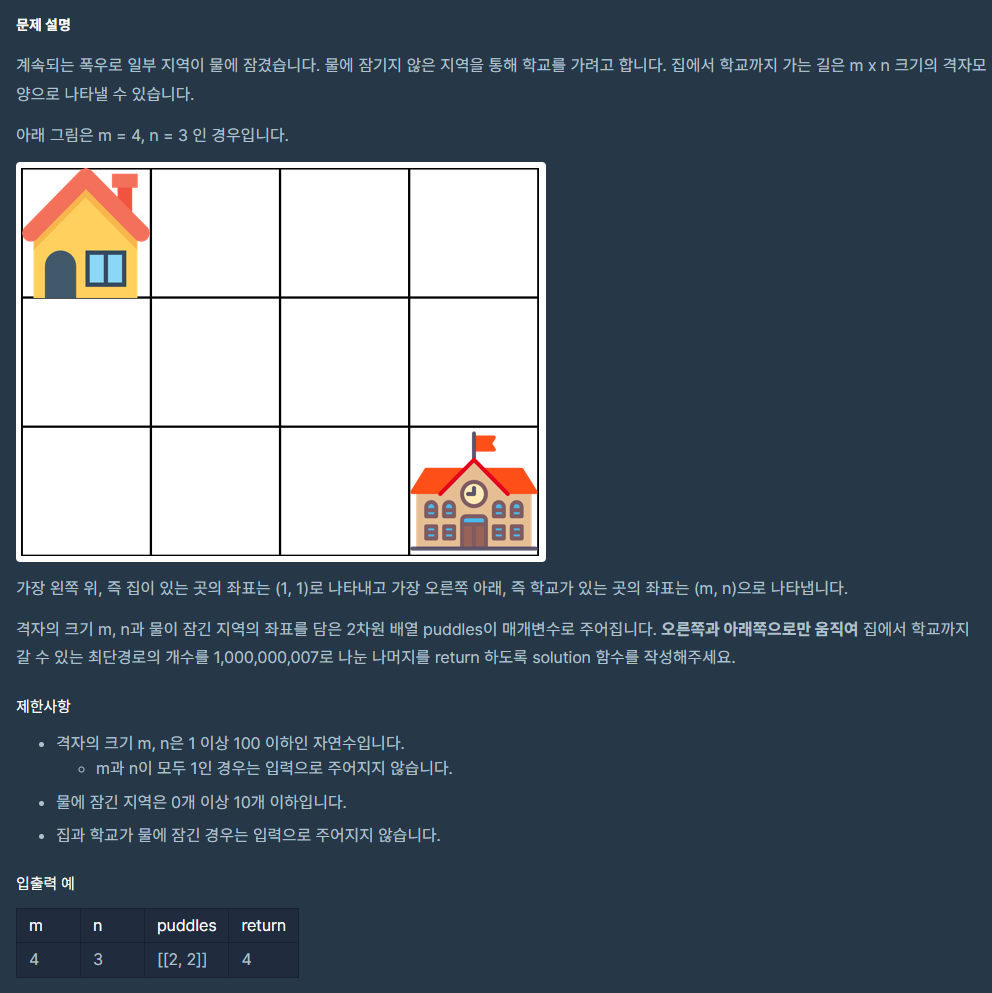
m*n 크기의 map 배열을 만들어서
map[m][n] 는 m,n에 갈 수 있는 경로의 수로 두고

map[m][n] = 왼쪽, 위쪽을 더한 값이므로 (오른쪽과 아래로 밖에 이동할 수 없기 때문에 왼쪽과 위쪽 칸의 경로 수를 더하면 된다)
map[m][n] = map[m-1][n] + map[m][n-1]을 하면 되겠지? 하고 바로 구현해봤다.

int getRouteCnt(vector<vector<int>>& map, int m, int n)
{
	//범위 밖이므로 0
    if (m < 0 || n < 0) return 0;
	
    //침수 구역은 못가므로 0
    if (map[m][n] == -1)
    {
        return 0;
    }
    
    //값이 존재한다면 return
    if (map[m][n] != -2)
    {
        return map[m][n] % 1000000007;
    }
	
    //아직 경로를 구하지 않은 칸을 만나면 경로를 구하여 return
    return getRouteCnt(map, m - 1, n) + getRouteCnt(map, m, n - 1);
}

int solution(int m, int n, vector<vector<int>> puddles) {
    int answer = 0;

    //-1 : 침수 -2 : 아직 구하지 않은 경우의 수
    vector<vector<int>> map(m, vector<int>(n, -2));

    map[0][0] = 1;

    //침수지역 -1로 초기화
    for (int i = 0; i < puddles.size(); i++)
    {
        map[puddles[i][0] - 1][puddles[i][1] - 1] = -1;
    }

    answer = getRouteCnt(map, m - 1, n - 1);

    return answer;
}

그 결과는?

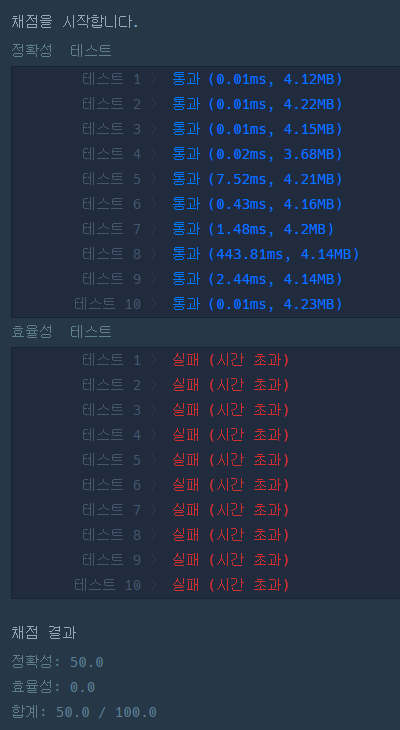
아.
100*100이라서 방심하고 그냥 쉽게쉽게 구했더니 재귀의 힘을 버티지 못하고 시간 초과가 떠버렸다.

흠.. 이러면 BFS를 한번 써보면 되겠다는 생각이 들었다.
인접한 노드가 아래와 오른쪽만으로 한정시키면 딱 현재 문제의 경우와 똑같다.
BFS로 탐색한다면 자연스레 왼쪽과 위쪽의 값이 존재하게 되므로
식은 원래 식과 동일하게 넣어주었다.

#include <string>
#include <vector>
#include <queue>

using namespace std;

int bfs(vector<vector<int>> &map, int m, int n)
{
    vector<vector<int>> isVisited(m+1,vector<int>(n+1, 0));
    queue<pair<int,int>> q;
    q.push({1,1});
    map[1][1] = 1;
    isVisited[1][1] = 1;
    
    //오른쪽, 아래
    int dx[2] = {1, 0};
    int dy[2] = {0, 1};
    
    while(!q.empty())
    {
        pair<int,int> cur = q.front();
        q.pop();
        
        for(int i=0;i<2;i++)
        {
            int nextX = cur.first + dx[i];
            int nextY = cur.second + dy[i];
            
            //범위 밖인 경우 제외
            if(nextX > m || nextY > n) continue;
            if(map[nextX][nextY] != -1 && isVisited[nextX][nextY] == 0)
            {
                q.push({nextX,nextY});
                isVisited[nextX][nextY] = 1;
                int up = ( map[nextX][nextY-1] == -1) ? 0 : map[nextX][nextY-1];
                int left = ( map[nextX-1][nextY] == -1) ? 0 : map[nextX-1][nextY];
                map[nextX][nextY] = (up + left) % 1000000007;
            }            
        }
    }
    
    return map[m][n];
}

int solution(int m, int n, vector<vector<int>> puddles) {
    int answer = 0;
    
    vector<vector<int>> map(m+1,vector<int>(n+1,0));
    
    //침수지역은 -1로 초기화
    for(int i=0;i<puddles.size();i++)
    {
        map[puddles[i][0]][puddles[i][1]] = -1;
    }

    answer = bfs(map, m, n);
    return answer;
}

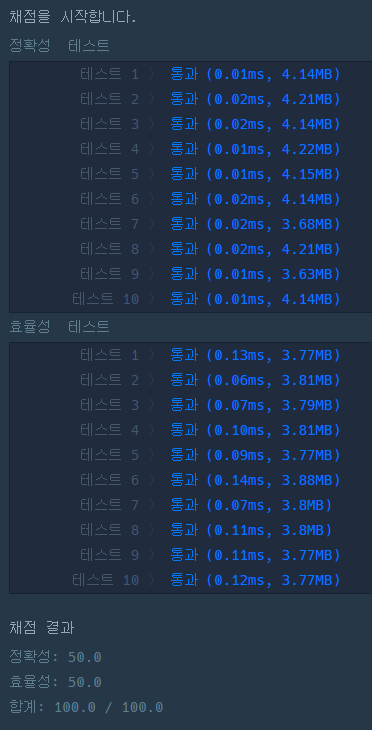
매우 빨라진 것을 확인할 수 있었다.

회고

생각나는 접근 방식 중에 가장 빠른 알고리즘을 생각해낼 수 있도록 하자..
그리고 실행시간에 대한 직관력이 더 필요하다.
물론 여기에는 몇초 이내라는 말이 명시되어있지는 않았지만
일단 재귀함수를 쓴 것은 별로 좋은 생각이 아니었던 것 같다.

BFS를 처음부터 썼더라면 참 깔끔하게 끝났을 것 같다.