배경

백준 알고르즘 문제를 풀다가 다익스트라 알고리즘을 처음 본지는 좀 됐지만... 너무 정리하기 귀찮아서 정리하지 않다가 같은 유형의 문제를 보게되어 이제서야 정리하게 된다.

이번에 날 괴롭힌 문제는 백준 5972번 번이다.
처음에 bfs로 최단거리를 풀려다가 시간초과로 에러를 출력했다.

개념

다익스트라(Dijkstra) 알고리즘은 DP을 활용한 대표적인 최단경로 탐색 알고리즘이다.
다익스트라 알고리즘이 DP에 속한 이유는 '최단거리는 여러 개의 최단 거리로 이루어져있기 때문'이다. 다만, 다익스트라의 특징은 하나의 최단거리를 구할 때 이전까지 구했던 최단 거리 정보를 그대로 사용한다는 특징이 있다.
작동원리는...
1. 출발 노드를 설정
2. 출발 노드를 기준으로 각 노드의 최소 비용을 저장
3. 방문하지 않은 노드 중에서 가장 비용이 적은 노드를 선택
4. 해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 최소 비용 갱신
5. 위 과정에서 3~4번을 반복
... 이와 같다.

글로만 봐서는 무슨 소리인지 나도 몰랐으니 간단한 예시를 통해 확인해보자!

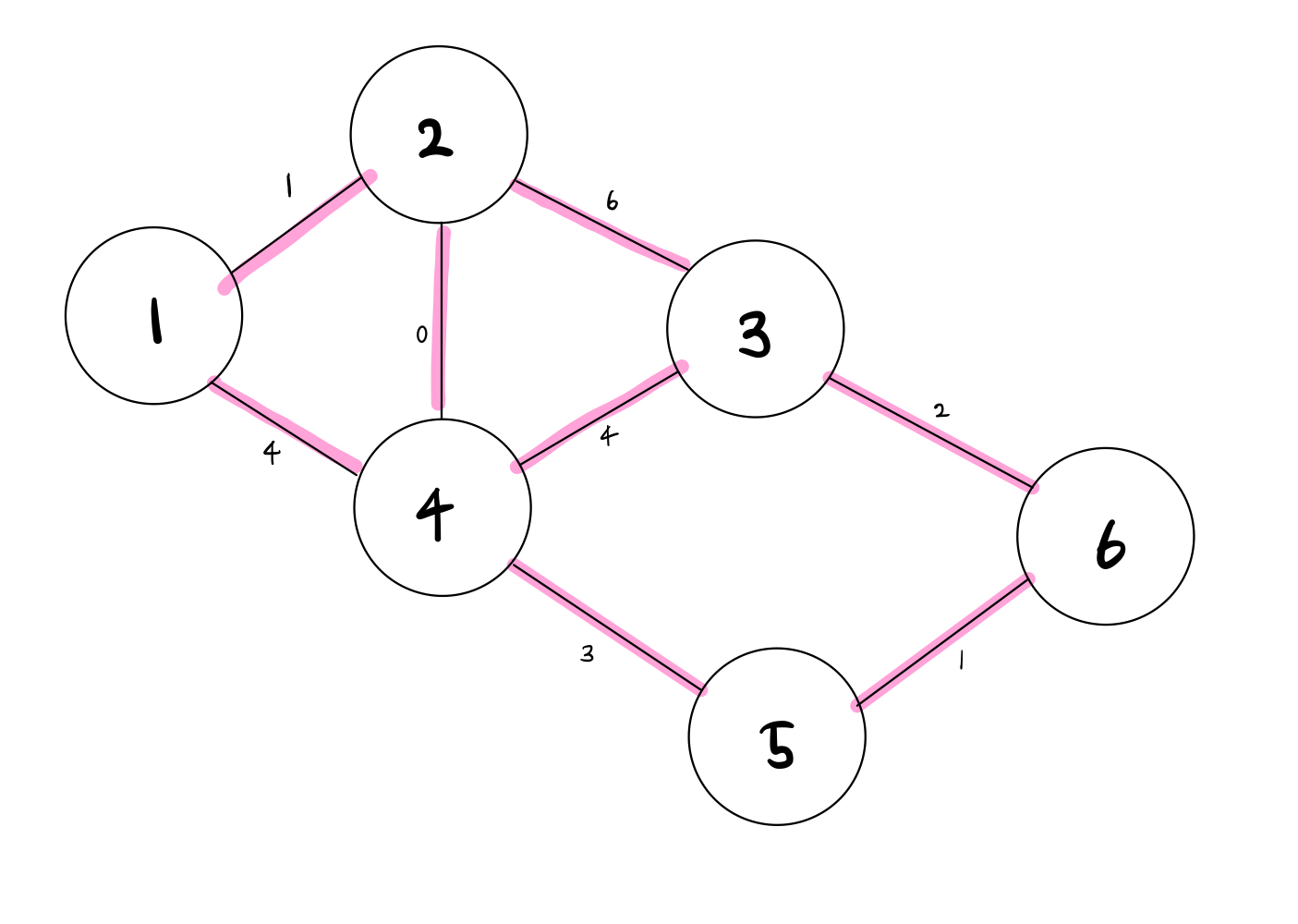
예시의 그림은 백준 5972번 Testcode를 그래프로 그려봤다.

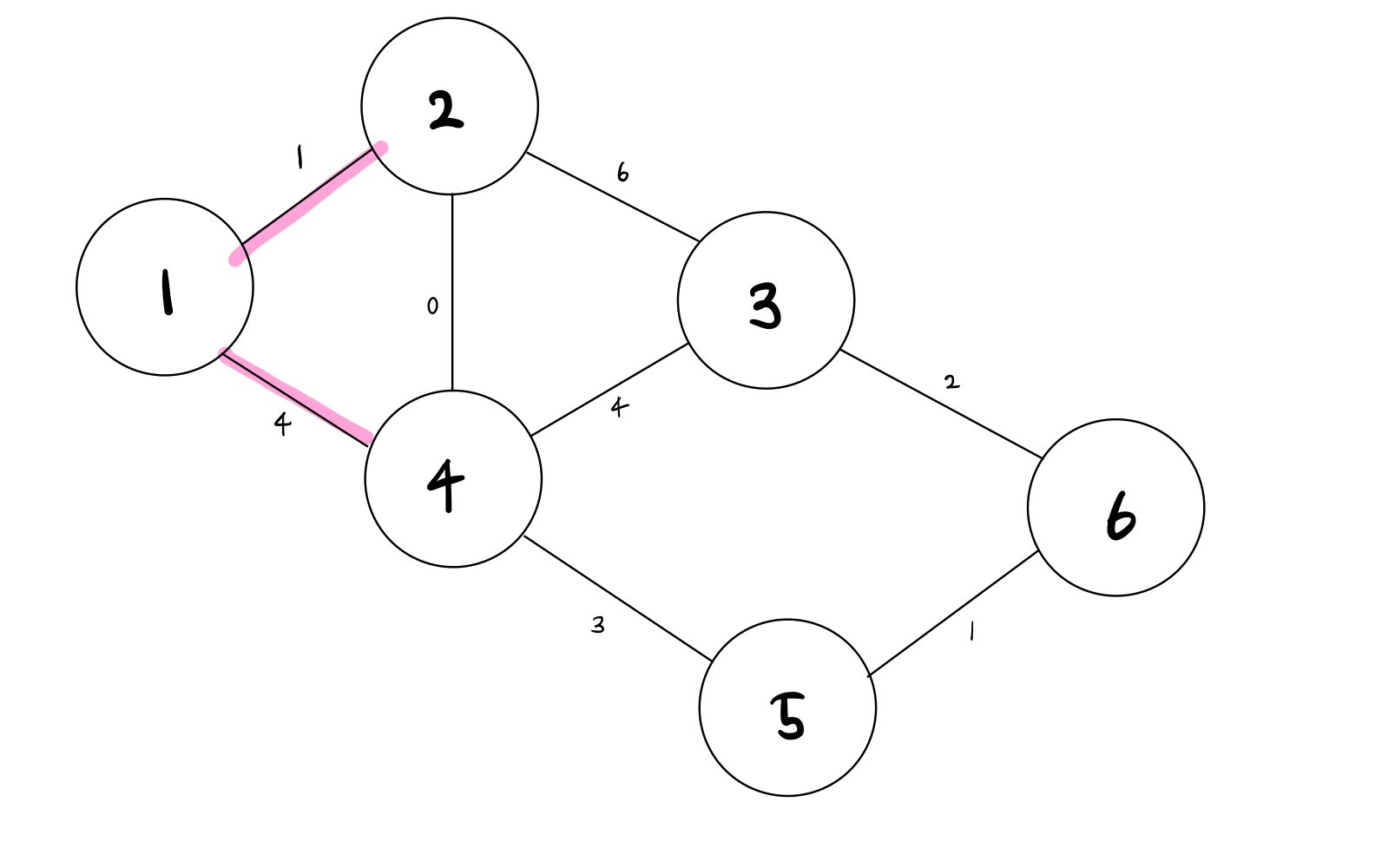
이 그래프를 표로 나타내면
(원래는 6x6으로 표현해야하나 문제에서 1에서 6으로의 최단거리를 구하고 있으니 이렇게 나타냈습니다.)

	1번노드	2번노드	3번노드	4번노드	5번노드	6번노드
1번 노드	0	1	INF	4	INF	INF

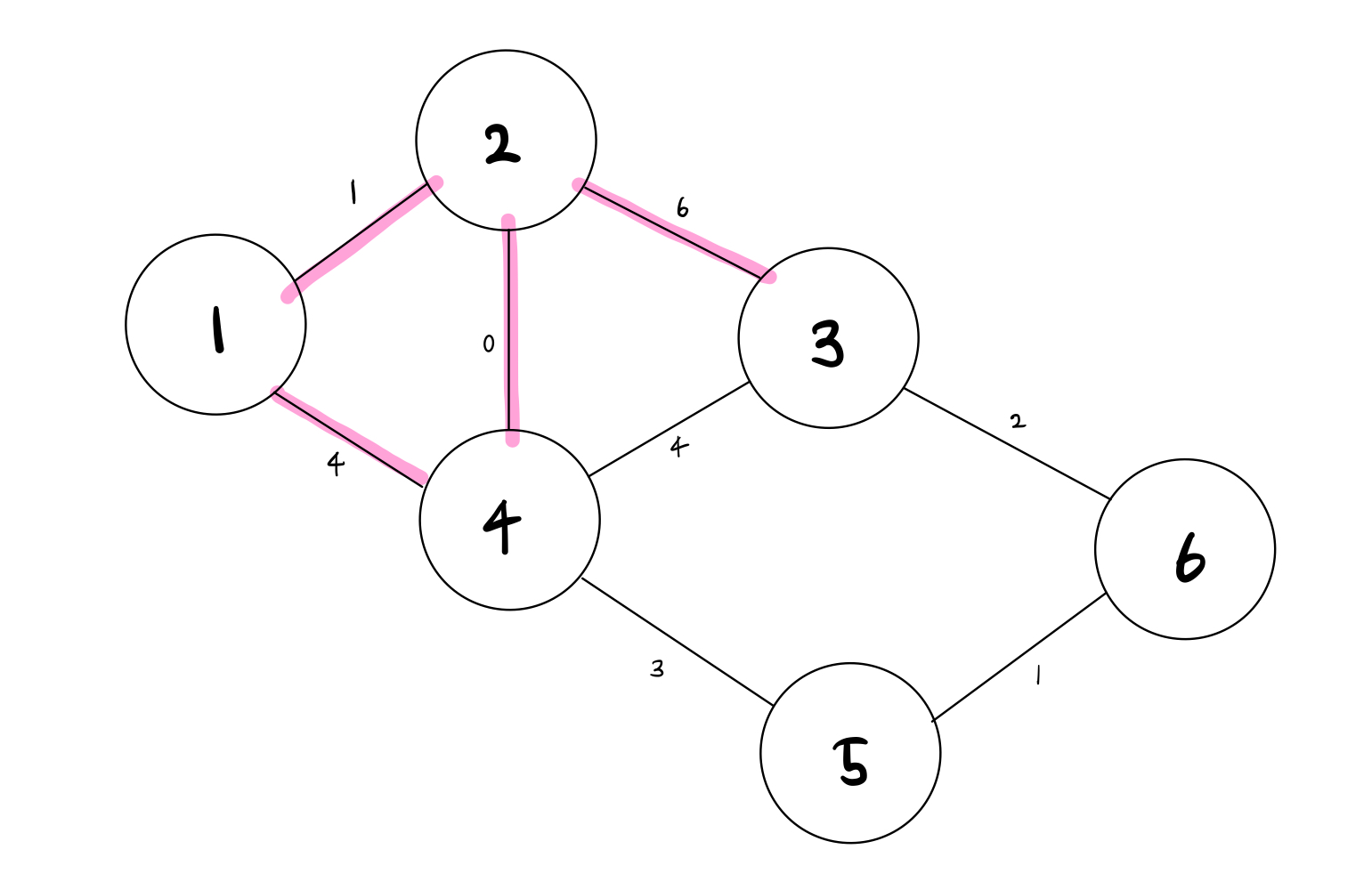
비용이 적은 노드는 2번노드이다.
이동하여 최소 비용을 갱신하면 다음 그래프와 같다.

	1번노드	2번노드	3번노드	4번노드	5번노드	6번노드
1번 노드	0	1	7	1	INF	INF

여기서 1에서 4번노드로 가는 값이 갱신된 이유는 기존보다 비용을 적게 내고 이동 할 수 있기 때문이다.

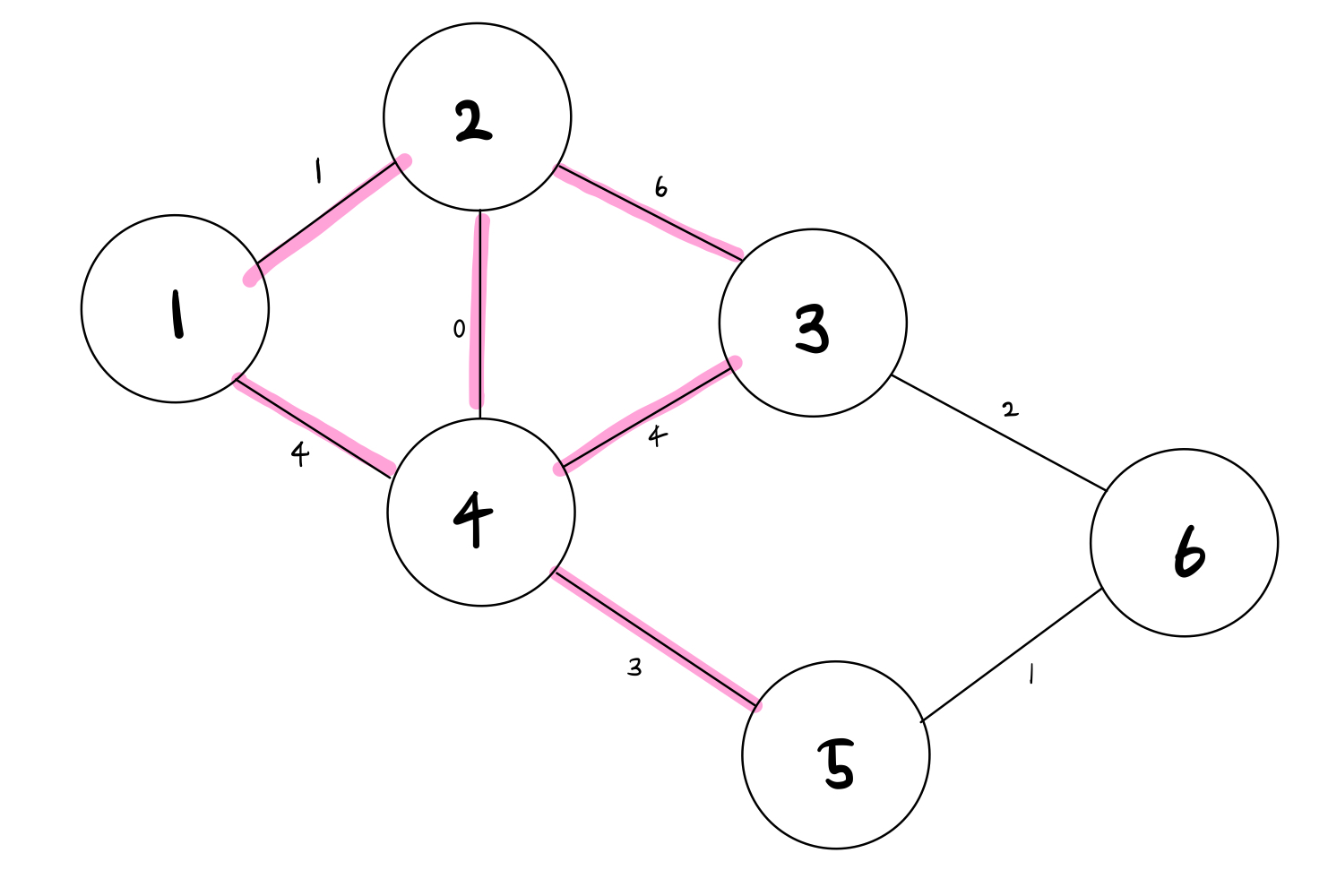
다시 방문하지 않은 노드 중에서 비용이 적은 노드(4번)를 선택하여 최소 비용을 갱신하면

	1번노드	2번노드	3번노드	4번노드	5번노드	6번노드
1번 노드	0	1	5	1	4	INF

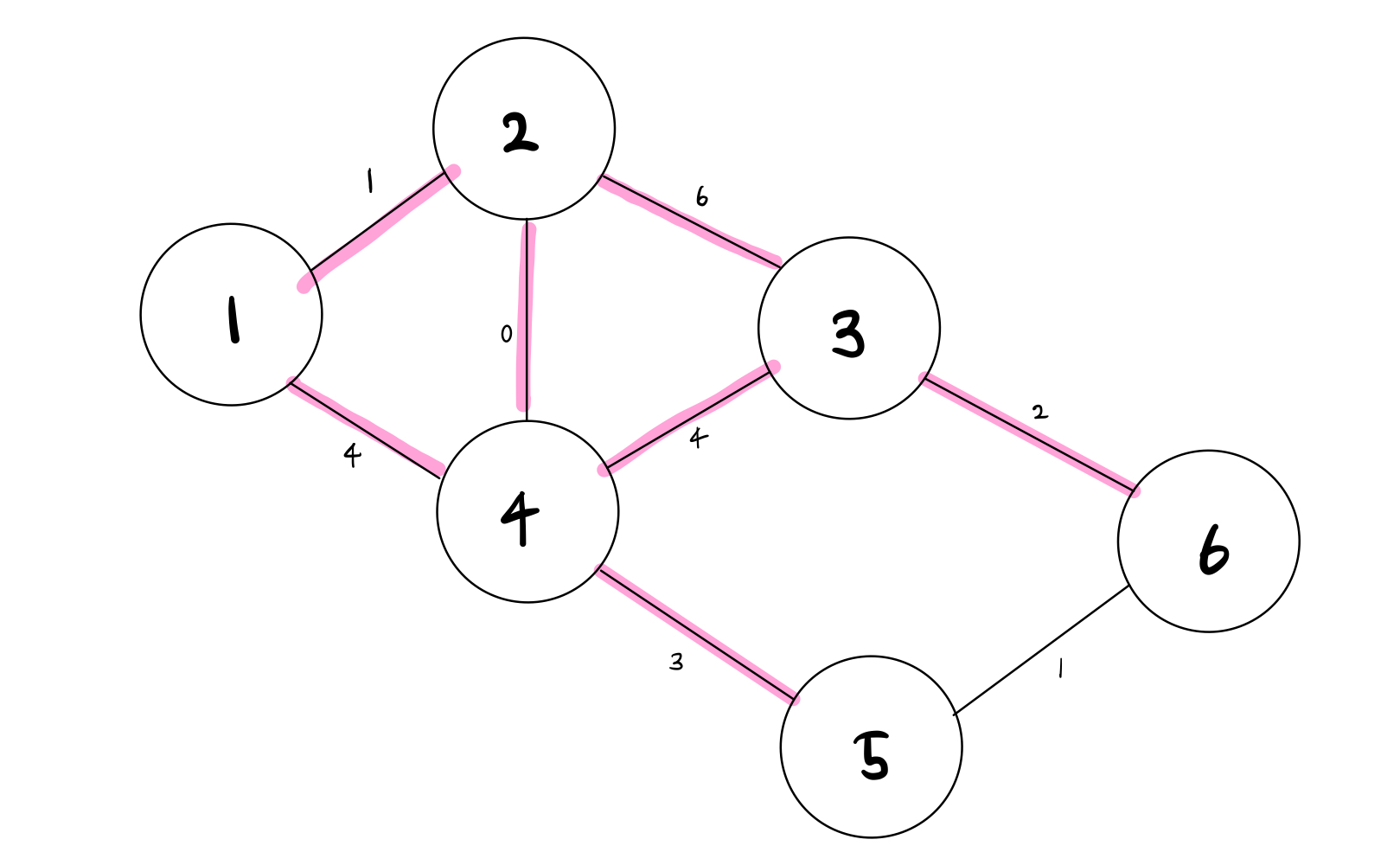
다시 방문하지 않은 노드 중에 비용이 적은 노드(3번)을 선택하여 최소 비용을 갱신한다.

	1번노드	2번노드	3번노드	4번노드	5번노드	6번노드
1번 노드	0	1	5	1	4	7

마지막으로 5번 노드, 6번노드를 방문하면 모든 노드가 갱신이 된다.

	1번노드	2번노드	3번노드	4번노드	5번노드	6번노드
1번 노드	0	1	5	1	4	5

구현

import sys, heapq
input = sys.stdin.readline

n,m = map(int,input().split())
INF = float("INF") # 무한대 상수 선언
graph = [[] for _ in range(n+1)] # 노드와 노드 사이의 거리를 담을 graph 리스트 선언
distance = [INF] * (n+1) # 거리를 최대값으로 만듬

for i in range(m): # 간선의 갯수만큼 
    a, b, c = map(int,input().split())
    graph[a].append((b,c))
    graph[b].append((a,c)) # 노드 위치와 비용순으로 graph에 집어넣습니다.

def dijkstra(s):
    q = []
    distance[s] = 0
    heapq.heappush(q,(0,s)) # q에 (거리, 위치) 를 담는다.
    while q:
        breakpoint()
        dist, cur = heapq.heappop(q) #거리와 현재위치
        if distance[cur] < dist: # 이미 계산돼 있는 최솟값보다 크다면 확인할 필요도 없으니 다음 반복으로 넘어갑니다.
            continue
        for next in graph[cur]:
            cost = dist + next[1]
            if cost < distance[next[0]]: # 이미 계산돼 있는 최솟값이 더 작았다면 갱신해줍니다.
                distance[next[0]] = cost # 갱신
                heapq.heappush(q,(cost,next[0])) # q에 (거리, 위치) 를 담는다.
    return distance[n] # 목적지의 최단거리를 리턴한다.

print(dijkstra(1))