배경

백준 문제를 풀다가 힙 정렬을 처음 보게 되었다.
힙 정렬과 파이썬 heapq 모듈을 안다면 쉽게 풀 수 있는 문제였지만 처음 보는 유형의 정렬이었기에 조금 당황했다...

다음에 당황하지 않기 위해 힙 정렬을 정리해보자!

개념

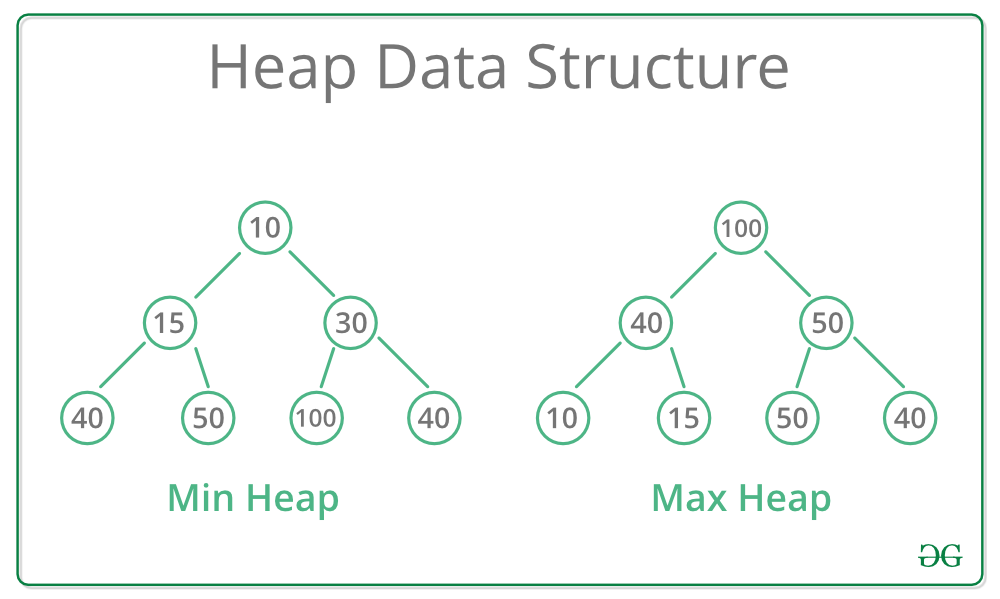
힙은 완전 이진 트리의 일종으로, 부모 노드의 값이 자식 노드의 값보다 크거나 작은 조건을 만족하는 자료구조 입니다.
그래서, 힙은 최대 힙(max heap) 또는 최소 힙(min heap)으로 구현됩니다.
힙은 주로 우선순위 큐를 구현하는데 사용되는데, 우선순위 큐는 시뮬레이션 시스템, 네트워크 트래픽 제어, 운영 체제에서의 작업 스케쥴링, 수치 해석적인 계산에 주로 사용합니다.

자료구조	삭제되는 요소
Stack	가장 최근에 들어온 데이터
Queue	가장 먼저 들어온 데이터
Priority Queue	가장 우선순위가 높은 데이터

출처: https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html

불안정 정렬이며, 힙을 사용하여 우선순위 큐를 구현하면 삽입과 삭제 연산이 평균적으로 O(log n)의 시간 복잡도를 갖습니다.

힙 정렬이란?

위에서 설명한 힙의 개념을 이용하여 정렬하는 알고리즘이다.
원리는 다음과 같습니다.

순서	내용
1	정렬할 리스트를 입력받는다.
2	리스트를 힙 구조로 변환한다.
3	힙에서 가장 큰 요소(루트 노드)를 추출한다.
4	추출한 요소를 정렬된 리스트에 추가한다.
5	힙의 크기를 줄이고, 다시 2단계부터 반복합니다.
6	힙이 비어있을 때까지 반복하여 정렬된 리스트를 얻습니다.

구현

# 힙을 구성하는 함수
def heapify(arr, n, i):
    largest = i  # 루트 노드를 가장 큰 값으로 설정
    left = 2 * i + 1  # 왼쪽 자식 노드
    right = 2 * i + 2  # 오른쪽 자식 노드

    # 왼쪽 자식 노드가 부모 노드보다 큰 경우
    if left < n and arr[i] < arr[left]:
        largest = left

    # 오른쪽 자식 노드가 부모 노드나 가장 큰 자식 노드보다 큰 경우
    if right < n and arr[largest] < arr[right]:
        largest = right

    # 가장 큰 노드를 부모 노드로 설정하고, 재귀적으로 힙을 구성
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)


# 힙 정렬 함수
def heap_sort(arr):
    n = len(arr)

    # 최대 힙을 구성
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)

    # 힙에서 요소를 하나씩 추출하여 정렬된 리스트에 추가
    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]  # 루트 노드와 맨 마지막 요소를 교환
        heapify(arr, i, 0)  # 힙 구성

출처 : https://colinch4.github.io/2023-09-01/16-25-24-157956/

위의 코드는 python으로 힙 정렬 알고리즘을 구현한 예시입니다. heapify 함수는 힙을 구성하기 위해 사용되고, heap_sort 함수는 힙 정렬을 수행합니다. arr 리스트에 정렬할 값들을 입력하고, heap_sort(arr)를 호출하여 정렬된 결과를 얻을 수 있습니다.

# 힙 정렬 사용 예시
arr = [12, 11, 13, 5, 6, 7]
sorted_arr = heap_sort(arr)
print("정렬된 배열:", sorted_arr)