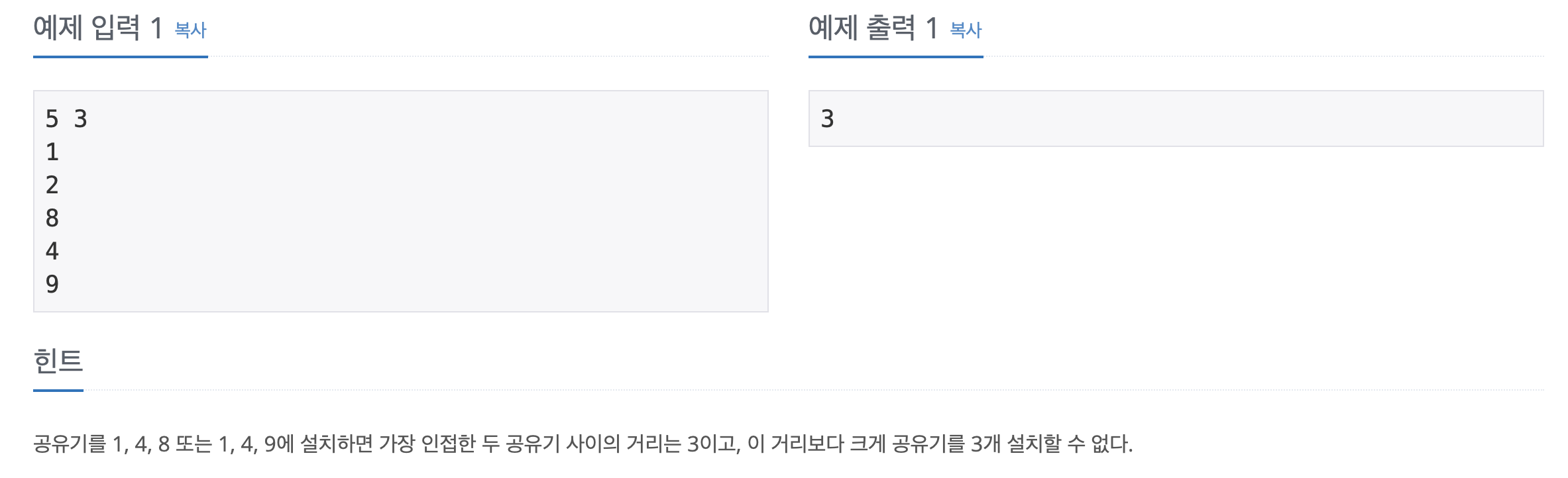
1️⃣ 문제 설명

백준 2110번 공유기 설치 풀러가기

입력값의 범위가 큰 것을 통해 이진 탐색 문제라는 힌트를 얻을 수 있다.

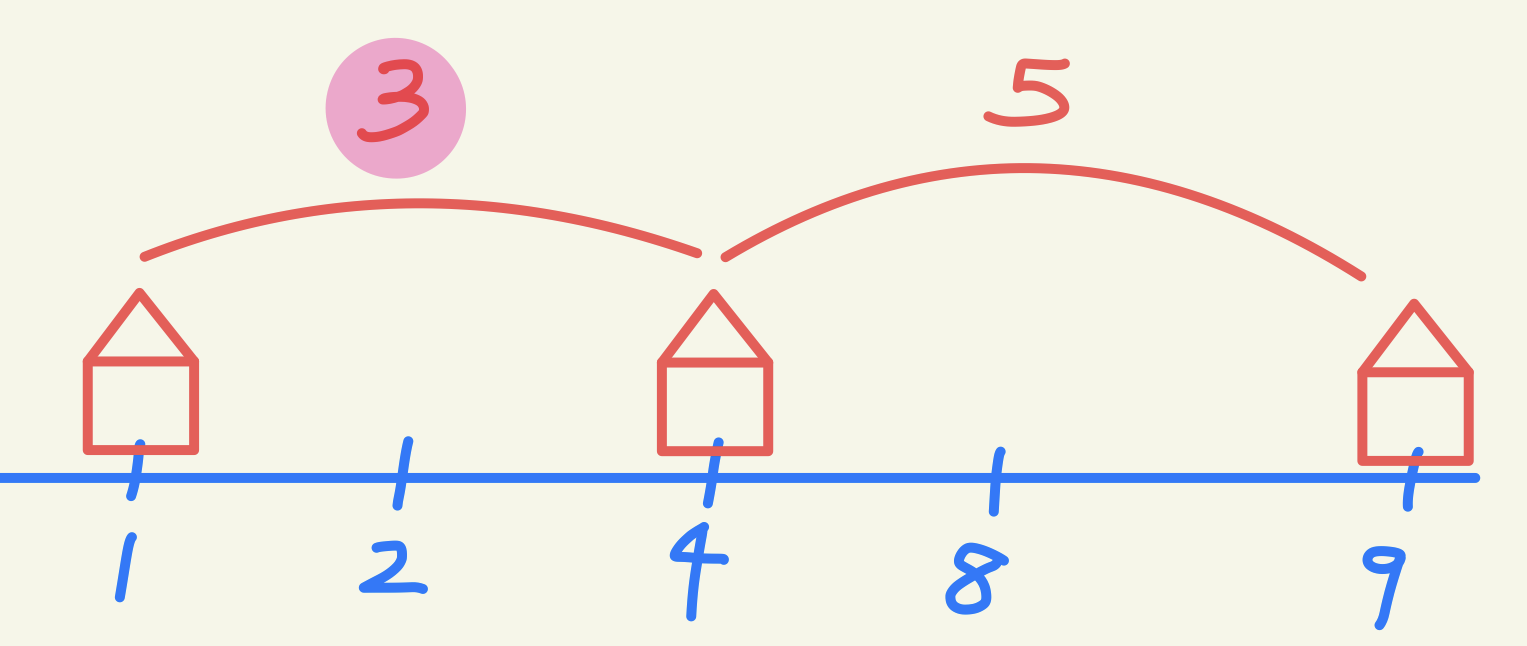
1️⃣ 1트 - 틀렸습니다

🍋 아이디어

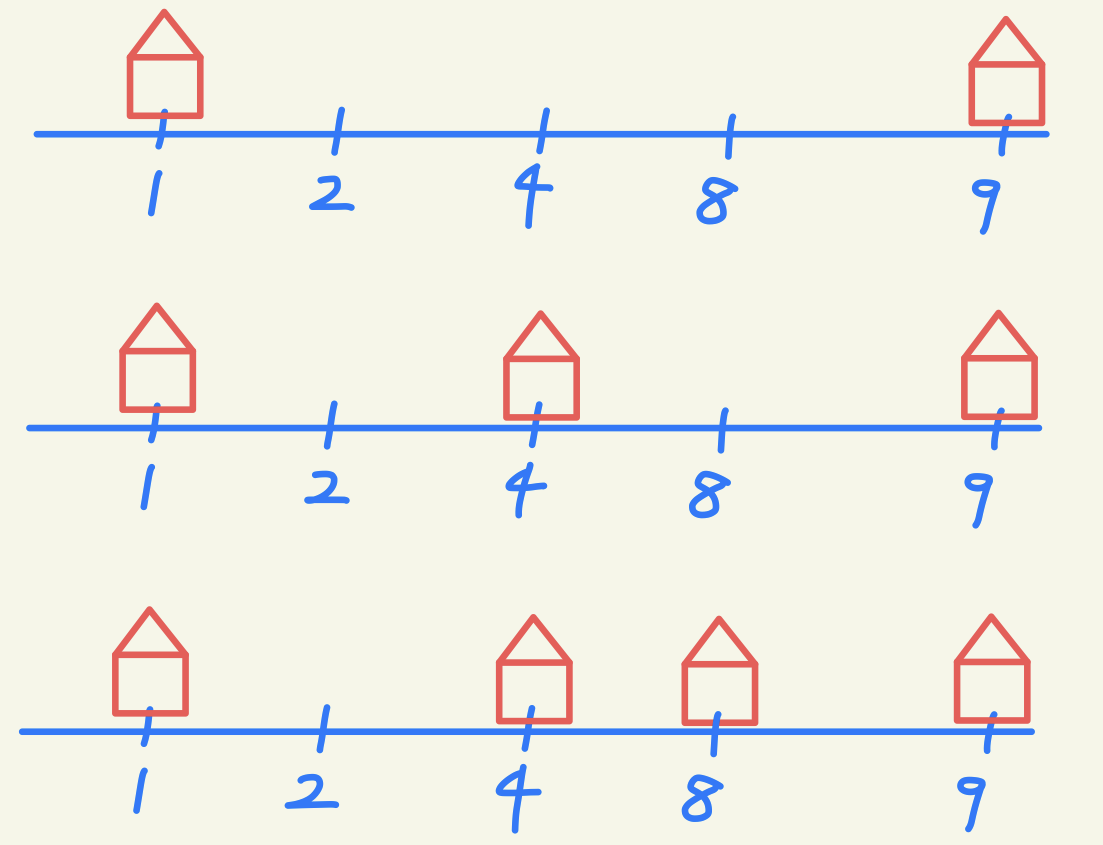
• 공유기를 설치할 집의 위치를 start, end, mid로 한다.
• 이진 탐색을 하며 집 사이 거리가 최대가 되도록 집들을 배치한다.
• 언제까지? C개를 모두 설치할 때까지
  
  
• 설치를 완료한 뒤, 설치된 집들의 좌표를 비교하여 최소값을 출력하자

🍋 전체 코드

import sys

input = sys.stdin.readline

INF = 1e9

n, c = map(int, input().split())

home = [] # 집의 위치
wifi = [] # 공유기를 설치한 집의 위치

for _ in range(n):
    home.append(int(input()))

# 이진 탐색이 가능하기 위해서는 리스트가 정렬되어 있어야 한다.
home.sort()

start = 0
end = len(home) - 1

# 초기값 대입 후 이진 탐색을 진행
wifi.append(home[start])
wifi.append(home[end])

while start < end and len(wifi) < c:
    mid = (start + end) // 2
    wifi.append(home[mid]) # 공유기 설치

	# 두 구간 중 더 길이가 긴 곳을 선택하여 이진 탐색 진행
    if (home[mid] - home[start]) > (home[end]-home[mid]):
        end = mid
    elif (home[mid] - home[start]) < (home[end]-home[mid]):
        start = mid
    else:
        if (mid - start) > (end - mid):
            end = mid
        else:
            start = mid

ans = INF

# 공유기가 설치된 집들 사이의 최소 거리를 구함
wifi.sort()
for i in range(len(wifi)-1):
    if wifi[i+1] - wifi[i] < ans:
        ans = wifi[i+1] - wifi[i]

print(ans)

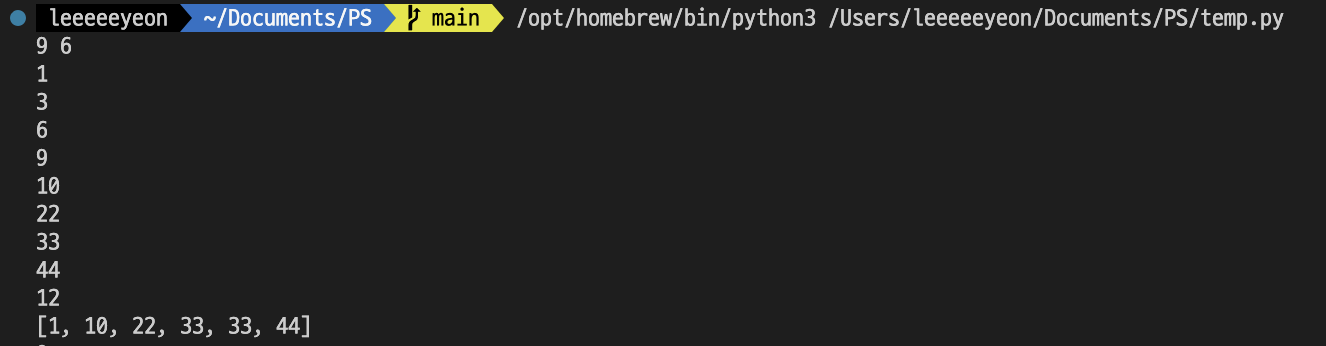
가장 아래 있는 리스트는 이진 탐색을 마친 후 wifi 리스트를 출력한 결과이다.
사진에서 33에 있는 집이 두 번 들어간 것처럼, 위와 같이 풀게 되면 start와 end 사이에 집이 더 없더라도 중복된 값이 들어가게 된다.

2️⃣ 2트 - 시간 초과

1트에서의 이진 탐색은 한 번 오른쪽 구간인 mid~end을 들어가게 되면 계속 오른쪽 구간으로 깊게 들어가게 된다.

🍋 아이디어

1트에서 있던 문제를 해결하기 위해 아래와 같은 아이디어를 떠올렸다.

만일 start와 end 사이에 공유기를 설치할 집이 없다면,

• 해당 구간을 벗어나고
• 비어 있는 새로운 구간으로 들어가서
• 다시 이진 탐색을 진행하여 집에 공유기를 설치한다
  
  
• 반복문을 추가하여 이미 공유기를 설치한 집은 home에서 지우고, C개의 공유기가 설치될 때까지 이진 탐색을 반복하자

🍋 전체 코드

import sys

input = sys.stdin.readline

INF = 1e9

n, c = map(int, input().split())

home = []
wifi = []
for _ in range(n):
    home.append(int(input()))

home.sort()

def binary_search(start, end, home):
    flag = 1
    start = 0
    end = len(home) - 1
    if start == 0 and end == 0:
        wifi.append(home[0])
        return flag

    while start < end and len(wifi) < c:
        mid = (start + end) // 2
        if mid == start or mid == end:
            if len(home) > 2:
                break
        wifi.append(home[mid])

        if (home[mid] - home[start]) > (home[end]-home[mid]):
            end = mid
        elif (home[mid] - home[start]) < (home[end]-home[mid]):
            start = mid
        else:
            if (mid - start) > (end - mid):
                end = mid
            else:
                start = mid

    return flag  

start = 0
end = len(home) - 1
flag = 0

wifi.append(home[start])
wifi.append(home[end])

while len(wifi) != c: # C개의 공유기를 설치 완료할 때까지
	# 이미 공유기를 설치한 집을 home 리스트에서 제거한 후
    if flag == 1:
        temp = set(home) - set(wifi)
        home = list(temp)
    # 이진 탐색을 반복한다
    flag = binary_search(start, end, home)

ans = INF
wifi.sort()
for i in range(len(wifi)-1):
    if wifi[i+1] - wifi[i] < ans:
        ans = wifi[i+1] - wifi[i]

print(ans)

• 이중 반복문을 사용하여 연산 횟수가 매우 많아진 것 같다

3️⃣ 3트 - 다른 사람 풀이 참고

🍋 아이디어

집 좌표가 아니라 가장 인접한 두 공유기 사이의 거리를 이진 탐색으로 결정한다

• start는 가장 인접한 두 공유기 사이의 거리의 최소값
• end는 가장 인접한 두 공유기 사이의 거리의 최대값
• mid는 가장 인접한 두 공유기 사이의 거리
  
  

1. 가장 인접한 두 공유기 사이의 거리를 mid라고 가정한다
2. mid로 했을 때 설치할 수 있는 공유기의 개수를 센다 → count
   ex 1) [1, 2, 4, 8, 9]에서 mid=2일 때: [1,4,8]에 공유기를 설치할 수 있음
   ex 2) [1, 2, 4, 8, 9]에서 mid=4일 때: [1,8]에 공유기를 설치할 수 있음

3-1. count가 c보다 크면, 공유기를 덜 세워야 한다. 공유기를 덜 세우기 위해 가장 인접한 두 공유기 사이의 거리를 늘리자. → mid가 커지는 방법으로 이진 탐색
3-2. count가 c보다 작으면, 공유기를 더 많이 세워야 한다는 뜻이다. 공유기를 더 많이 세우기 위해서는 가장 인접한 두 공유기 사이의 거리가 줄이자. → mid가 작아지는 방법으로 이진 탐색

🍋 전체 코드

import sys

input = sys.stdin.readline

n, c = map(int, input().split())

home = []

for _ in range(n):
    home.append(int(input()))

# 이분탐색의 기본은 정렬
home.sort()

start = 1 # 최소 거리
end = home[-1] - home[0] # 최대 거리

result = 0
# 집이 두 개라면 무조건 둘 사이의 거리
if c == 2:
    result = home[-1] - home[0]

else:
    while start < end:
        count = 1
        pre = home[0]
        mid = (start + end) // 2 # 공유기 사이의 거리

        for i in range(1, n):
            if home[i] - pre >= mid:
                count += 1
                pre = home[i]
        if count >= c:
            # c개보다 공유기를 더 많이 설치할 수 있음
            # 공유기 설치 개수를 줄여야 함
            # 집 사이 거리는 커져야 함
            start = mid + 1
            result = mid
        elif count < c:
            # 공유기 설치 개수를 늘려야 함
            # 집 사이 거리는 줄어들어야 함
            end = mid

print(result)

😱 헷갈렸던 부분

start <= end? start < end?

이번 문제뿐만 아니라 다른 이진 탐색 문제에서도 while문의 조건으로 start <= end를 사용한다. 나는 이때 왜 부등호가 붙는지 잘 이해가 안되었는데!
smart & kind 동동이 이해가 잘 되게 설명을 해주었다.

[27, 31, 37]이라는 리스트에서 37을 찾는 것을 예시로 들어보자.

인덱스	9	10	11
원소	27	31	37
포인터	start	mid	end

우리가 찾는 37이 mid에 있는 31보다 크기 때문에 start = mid+1로 해주자.

인덱스	9	10	11
원소	27	31	37
포인터	start		start, mid, end

start = mid+1로 변경해준 뒤, 다시 mid를 구하면 세 포인터 변수의 위치는 위와 같다. 이제 mid에 있는 값이 우리가 찾는 값이니 찾았다!라고 외치고 반환하면 된다.

근데 만약 while 문의 조건이 start < end라면 찾았다!를 하지 못하니 우리는 37을 찾지 못하게 된다 ...

하지만 while 문의 조건이 start <= end라면 우리는 37을 확인하고 찾았다!를 외칠 수 있게 된다.

왜 start = mid가 아니라 mid + 1일까?

start와 mid가 의미하는 바를 다시 상기하자.
start는 공유기 사이의 최소 거리이고, mid는 공유기 사이의 거리이다.
count >= c일 때 mid보다 공유기 사이의 거리가 커야 한다는 걸 알았으니 mid보다 더 커야 한다. 그러므로 mid가 아닌 mid+1이다

왜 count == c를 따로 빼면 틀릴까?

갯수를 만족하더라도 최소 거리가 더 커질 수 있다!
그러니 오 3개 찾았다ㅋㅋ하고 바로 답 출력을 하면 안된다. 우리는 가장 인접한 두 공유기 사이의 최대 거리( = 최소 거리의 최대값)을 찾는 것이므로 더 커질 수 있는지 확인하자!

---

👻 TMI

이번 문제에서 나는 처음 시도를 할 때 부수적인 요소인 집의 위치를 로직의 핵심으로 잡아 리스트를 만들고, 리스트를 가공하여 답을 얻어냈다.

하지만 처음부터 위치가 아니라 답인 거리를 핵심으로 잡아서 푸는게 중요한 것이었다.

이번 문제뿐만 아니라 이제까지 문제를 풀며 내가 떠올리던 대부분의 아이디어는 문제를 풀기 위한 부수적인 요소를 활용하여 무언가를 만들고, 그것을 가공하여 답을 도출해냈다.

이번 문제를 풀며 부수적인 요소를 로직의 핵심으로 잡으면 떠올리기는 쉬워도, 구현해야 할 코드가 많아진다는 것을 뼈저리게 느낄 수 있었다.

조금 오래 걸리더라도 답에서 명시하고 있는 것을 핵심 변수로 하는 풀이 방법을 떠올리는 연습을 하자