구간 합, 부분 합, 누적 합

• 부분 합(= 누적 합) - 0~b까지 원소의 합
• 구간 합 - a~b까지 원소의 합

구간 합, 부분 합, 누적 합을 사용하면 배열의 일부 구간에 대한 합을 매우 빠르게 구할 수 있다.

N개의 원소로 이루어진 배열이 주어졌을 때,

• 반복문을 돌며 부분 배열의 합을 구하면 O(N)이 걸리지만
• 부분합을 이용하면 모든 부분합을 O(1)에 바로 구할 수 있다.

---

1차원 배열

Index	0	1	2	3	4	5	6
Element	2	4	1	-5	2	-3
Prefix Sum	0	2	6	7	2	4	1

sum[i] = arr[0] + arr[1] + ... + arr[i-1] 라고 생각하면 된다.

이 때 i번째 항부터 j번째 항까지의 합을 $S(i,j)$라고 하면,
S(i,j) = sum[j+1] - sum[i] 라고 할 수 있다.

예를 들어, 2번째 항부터 4번째 항까지의 합을 구해보자.

• 평범하게 구간합을 구하면, arr[2] + arr[3] + arr[4] = 1 + (-5) + 2 = -2
• 공식을 사용하면, S(2, 4) = sum[5] - sum[2] = 4 - 6 = -2

로 결과가 동일하다는 것을 알 수 있다.

코드

n = 6
data [2, 4, 1, -5, 2, -3]

sum_value = 0
prefix_sum = [0]

# 부분 합
for i in data:
	sum_value += i
    prefix_sum.append(sum_value)
    
# 구간 합
i = 2
j = 4
print(prefix_sum[j+1] - prefix_sum[i]) # 결과: -2

---

2차원 배열

sum[i][j] = arr[0][0] + ... + arr[i-1][j-1] 이다.
그리고 이것을 점화식으로 나타내면,
sum[i][j] = arr[i-1][j-1] + sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] 이다.

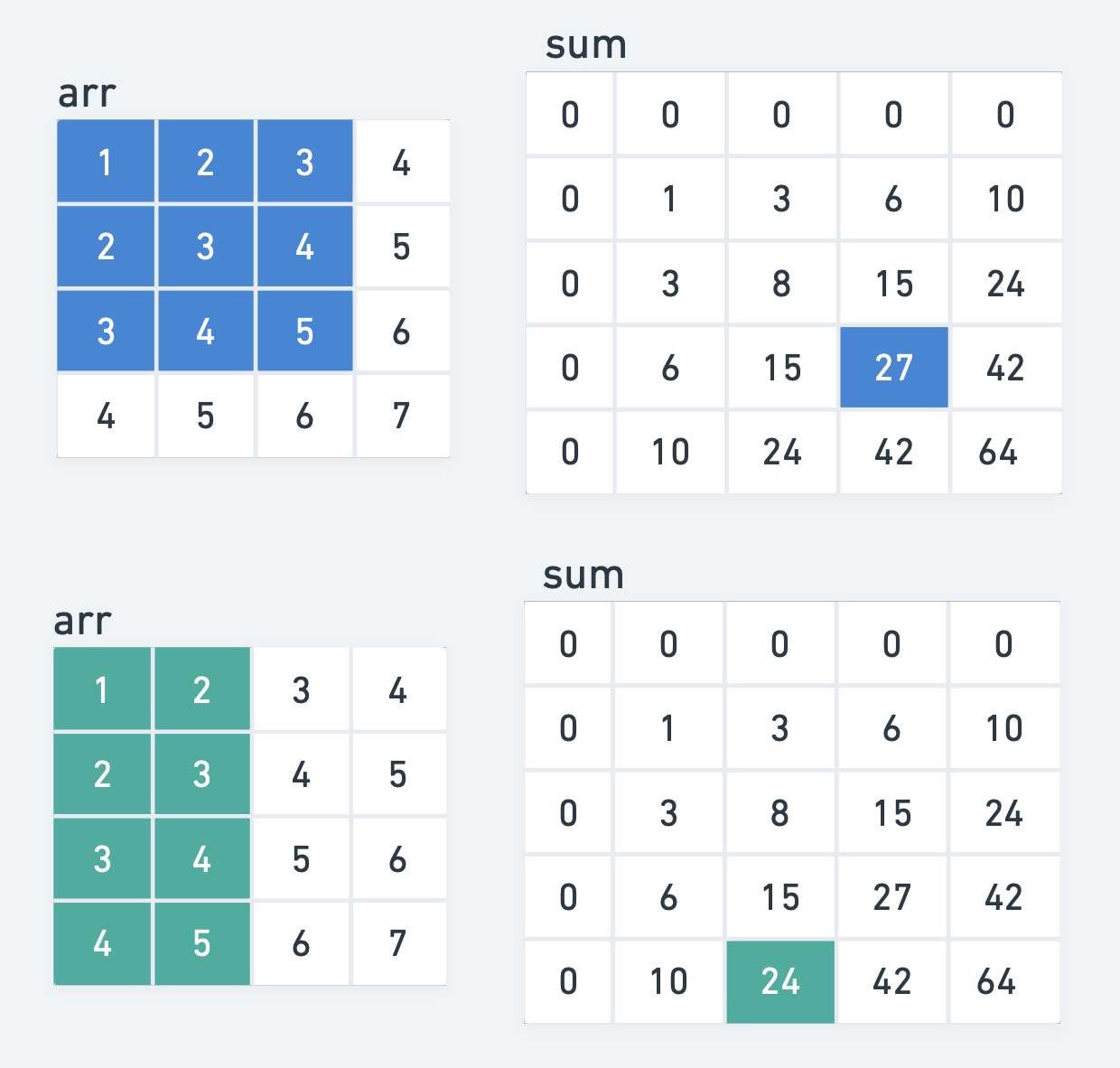
arr 리스트가 왼쪽과 같을 때, sum 리스트는 오른쪽과 같다.

첫 번째는 sum[3][3], 두 번째는 sum[4][2]일 때의 예이다.

sum[4][2]를 예로 들면,

sum[4][2]
= arr[0][0] + arr[0][1] + arr[1][0] + arr[1][1] + arr[2][0] + arr[2][1] + arr[3][0] + arr[3][1] + arr[4][0] + arr[4][1]
= arr[3][1] + sum[3][2] + sum[4][1] - sum[3][1]

를 의미한다.

부분 합으로 구간 합 구하기

여기서, (x1, y1)부터 (x2, y2)까지의 구간 합을 S라고 하면,
S = sum[x2+1][y2+1] - sum[x1][y2+1] - sum[x2+1][y1] + sum[x1+1][y1+1] 으로 구할 수 있다.

아래 사진처럼 (1,1)부터 (2,3)까지의 구간 합을 구하는 상황을 가정해보면,

S = sum[3][4] - sum[1][4] - sum[3][1] + sum[2][2]
= 42 - 6 - 10 + 1 = 27

로 구할 수 있다.
이는 3 + 4 + 4 + 5 + 5 + 6 = 27 과 동일한 결과이다.

코드

arr = [[1,2,3,4],[2,3,4,5],[3,4,5,6]]
        
m, n = 4, 3 # 가로, 세로 길이

sum_arr = [[0 for _ in range(m+1)] for _ in range(n+1)]

# 부분 합
for i in range(1, n+1):
    for j in range(1, m+1):
        sum_arr[i][j] = arr[i-1][j-1] + sum_arr[i-1][j] + sum_arr[i][j-1] - sum_arr[i-1][j-1]
        
for elem in sum_arr:
	print(elem)
    
# 구간 합
x1, y1 = 1,1
x2, y2 = 2,3
print(f'\n\n{x1, y1}부터 {x2, y2}까지의 구간 합: ', end = '')
print(sum_arr[x2+1][y2+1] - sum_arr[x1][y2+1] - sum_arr[x2+1][y1] + sum_arr[x1][y1])
# (1, 1)부터 (2, 3)까지의 구간 합: 27

    
# arr: 
# [1, 2, 3, 4]
# [2, 3, 4, 5]
# [3, 4, 5, 6]

# sum_arr:
# [0, 0, 0, 0, 0]
# [0, 1, 3, 6, 10]
# [0, 3, 8, 15, 24]
# [0, 6, 15, 27, 42]

활용 문제

[백준 11660번] 구간 합 구하기 5
[백준 21318번] 피아노 체조
[백준 10986번] 나머지 합
[프로그래머스] 파괴되지 않은 건물