1️⃣ 백트래킹이란?

• 모든 가능한 경우의 수 중에서 특정한 조건을 만족하는 경우만 살펴보는 알고리즘

현재 상태에서 가능한 모든 경로를 따라 들어가 탐색하다, 원하는 값과 불일치하는 부분이 발생하면 더 이상 탐색을 진행하지 않고 전 단계로 돌아간다

2️⃣ 백트래킹과 DFS의 차이

백트래킹은 불필요한 탐색을 하지 않는 반면, DFS는 모든 경우의 수를 탐색한다.
A = [132, 234, 123]이라는 배열이 있고, 123이라는 값을 찾고 있다고 해보자.

132라는 값에 접근했을 때 백트래킹과 DFS의 차이를 보자.

• 백트래킹 - 백의 자리는 동일하나, 십의 자리는 다르기 때문에 더 이상 탐색을 진행하지 않고 다음 수로 넘어간다.
• DFS - 십의 자리에 접근했을 때 원하는 수가 아님에도 불구하고 일의 자리 수까지 탐색한다.
  • 즉 트리의 바닥에 도달할 때까지 탐색을 계속한다.

3️⃣ 기본 문제 - N과 M (1)

백트래킹 기본 문제인 N과 M (1)으로 백트래킹 알고리즘을 이해해보자.

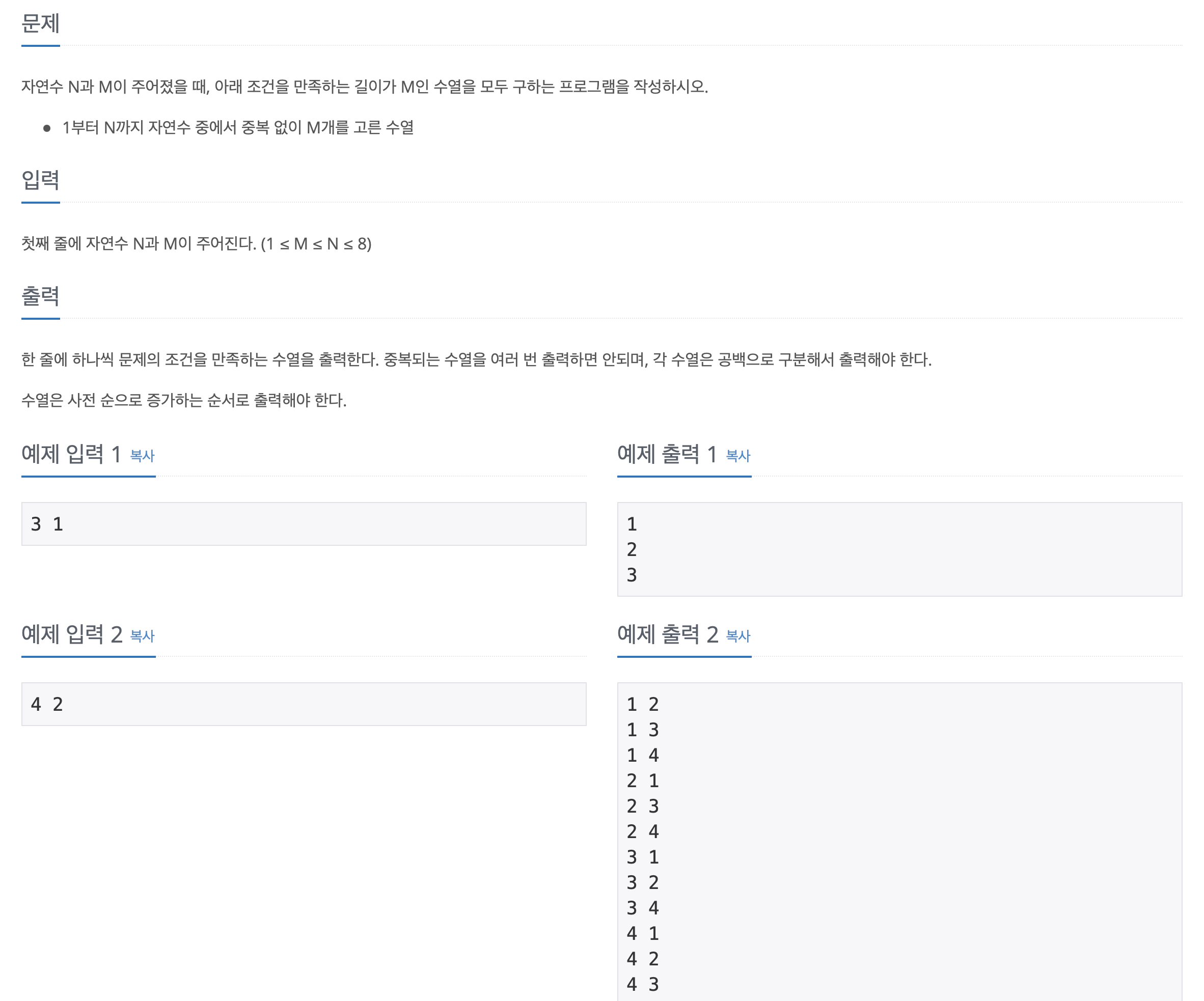
N = 4, M = 3을 예시로 하여 수열을 하나씩 찾아가는 과정 중 일부를 그림으로 표현하면 아래와 같다.

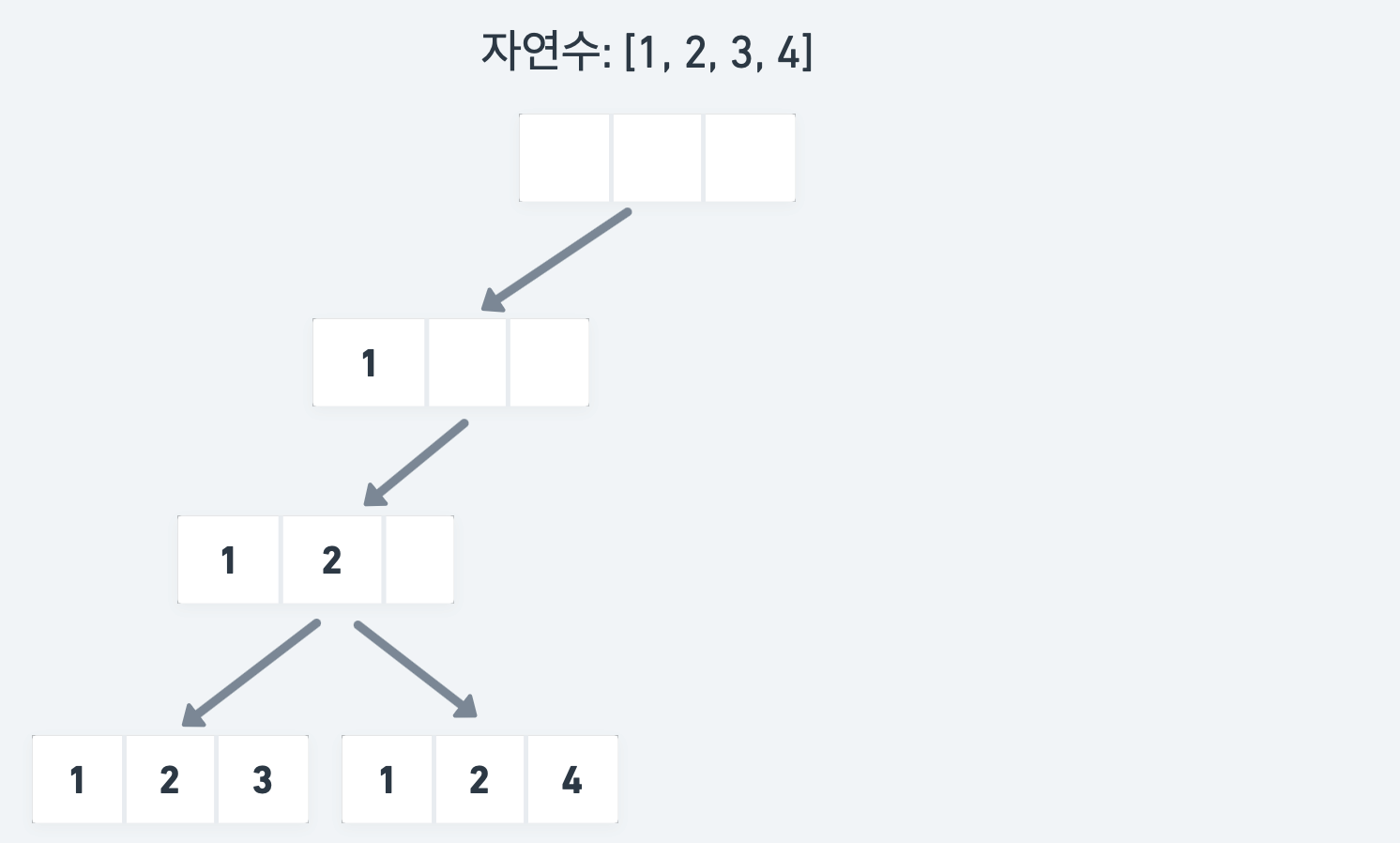
1. 빈 리스트에 1을 채워넣는다.
2. 리스트의 길이가 M이 될 때까지, 사용하지 않은 수 중 하나를 꺼내 리스트에 담는다. (2 선택 > 3 선택)
3. 모든 칸이 찼으면, 리스트를 출력하고 이전 상태로 돌아간다.
4. 사용하지 않은 수 중 하나를 꺼내 리스트에 담는다.
   ... (반복)

3번 과정에서 리스트가 가득 찼기 때문에 이전 상태로 돌아가는 과정이 백트래킹의 핵심이다.
✨탐색을 멈추고 전 단계로 돌아간다✨

이를 코드로 나타내면 아래와 같다.

import sys

input = sys.stdin.readline

n, m = map(int, input().split())

arr = [0 for i in range(m)] # 1부터 M까지의 
issued = [False for i in range(n+1)] # 방문 여부를 담은 리스트

# 재귀를 통해 리스트를 채워나간다.
def func(k): # k - 현재 리스트의 길이
    if k == m: # 리스트가 가득 차면 리스트의 원소를 출력한다.
        for elem in arr:
            print(elem, end=' ')
        print()
        return

    for i in range(1, n+1):
        if not issued[i]: # 방문하지 않은 자연수에 대해
            arr[k] = i # 리스트에 담고
            issued[i] = True # 방문 처리를 해준다
            func(k+1)
            issued[i] = False
            # 해당 줄까지 도착했으면, 트리의 바닥까지 탐색을 완료한 것이므로
            # False로 되돌려 이전 단계로 돌아갈 수 있도록 한다.

func(0)

백트래킹을 할 때, 이전 단계로 되돌아갈 수 있도록 사용했던 값을 False로 되돌려주는 과정도 까먹으면 안된다!

4️⃣ 일반적인 백트래킹 알고리즘

정리하면, 백트래킹 알고리즘은 크게 두 가지 과정으로 나눌 수 있다.

• 유망한지 판단 (promising)
  • 방문 중인 노드에서 하위 노드가 해답을 발견할 가능성이 있는 것을 유망하다고 한다.
• 가지치기 (pruning)
  • 유망하지 않으면, 하위 트리를 가지치기한다.

def backtracking(node v):
	node u
    if promising(v):
    	if (v에 해답이 있으면):
        	print(해답)
        else:
        	for(v의 모든 자식 노드 u에 대해서):
            	backtracking(u)
    

5️⃣ 응용 문제 - N-Queen

백트래킹을 응용한 대표적인 문제로는 백준 9663번 N-Queen이 있다.
해당 문제에 대해서는 이전 글에서 다룬 적이 있으므로 설명을 생략한다.

✨ Reference

https://blog.encrypted.gg/945
https://veggie-garden.tistory.com/24