AIFFEL FD #14 비지도학습 Unsupervised Learning

이재준·2021년 7월 30일

목록 보기

15/25

✅ 핵심내용

비지도학습(Unsupervised Learning)
클러스터링 - K-means, DBSCAN
차원 축소 - PCA, T-SNE

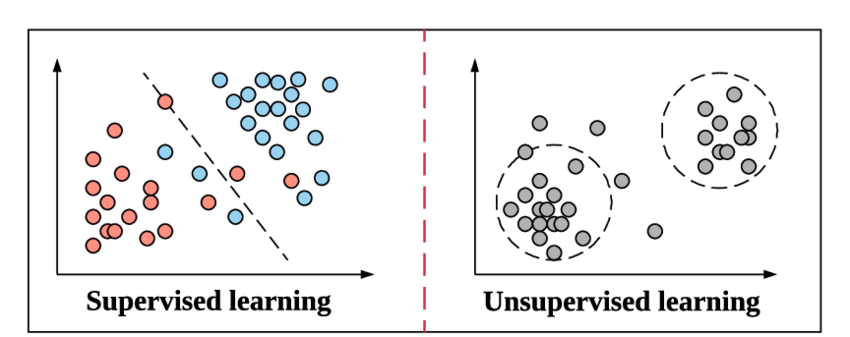
비지도학습 Unsupervised learning

데이터셋은 라벨링이 되어 있지 않은 경우, 라벨링이 되어 있는 데이터셋을 마련하기 위해 많은 인적 자원이 필요하다. 이 문제를 해결하기 위해, 라벨링이 되어 있지 않은 데이터들 내에서 비슷한 특징이나 패턴을 가진 데이터들끼리 군집화 하는 비지도학습이 제시되었다.

비지도학습(Unsupervised learning) 이란, 지도학습과 달리 training data로 정답(label)이 없는 데이터가 주어지는 학습방법이다.

비지도학습은

군집화 (클러스터링, clustering) : K-means, DBSACAN 알고리즘
차원 축소(dimensionality reduction) : PCA(Principal Component Analysis), T-SNE 방법

등 정답이 없는 데이터를 이용한 학습 전체를 포괄한다.

클러스터링 - K-means

K-means 알고리즘은 k 값이 주어져 있을 때, 주어진 데이터들을 k 개의 클러스터로 묶는 알고리즘으로 대표적인 클러스터링 기법 중 하나이다.

전체적인 K-mean 알고리즘의 순서는 다음과 같이 구성된다.

1. 원하는 클러스터의 수(K)를 결정
1. 무작위로 클러스터의 수와 같은 K개의 중심점(centroid)을 선정. 이들은 각각의 클러스터를 대표
1. 나머지 점들과 모든 중심점 간의 유클리드 거리를 계산한 후, 가장 가까운 거리를 가지는 중심점의 클러스터에 속하도록 함
1. 각 K개의 클러스터의 중심점을 재조정. 특정 클러스터에 속하는 모든 점들의 평균값이 해당 클러스터 다음 iteration의 중심점이 됨.(이 중심점은 실제로 존재하는 데이터가 아니어도 상관없음)
1. 재조정된 중심점을 바탕으로 모든 점들과 새로 조정된 중심점 간의 유클리드 거리를 다시 계산한 후, 가장 가까운 거리를 가지는 클러스터에 해당 점을 재배정
1. 4번과 5번을 반복 수행. 반복의 횟수는 사용자가 적절히 조절하면 되고, 특정 iteration 이상이 되면 수렴(중심점이 더 이상 바뀌지 않음)하게 됨

위 과정의 자세한 코드를 아래의 GitHub 링크에 기록하였다.

GitHub Link : FD17_Unsupervised_Learning

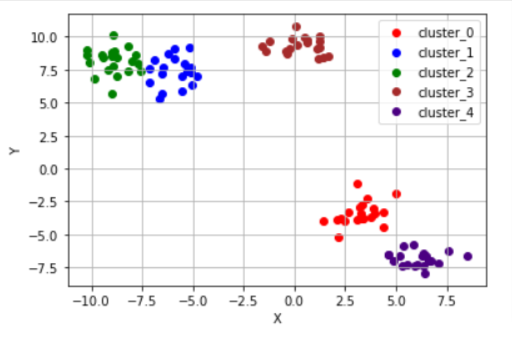
K-means 알고리즘이 잘 동작하지 않는 예시

K-means 알고리즘은 다음과 같은 상황에서는 적합하지 않은 군집화 알고리즘이다.

군집의 개수(K 값)를 미리 지정해야 하기 때문에 이를 알거나 예측하기 어려운 경우에는 사용하기 어려움
유클리드 거리가 가까운 데이터끼리 군집이 형성되기 때문에 데이터의 분포에 따라 유클리드 거리가 멀면서 밀접하게 연관되어 있는 데이터들의 군집화를 성공적으로 수행하지 못함

아래는 K-means 알고리즘이 잘 동작하지 않는 예시이다.

가운데 작은 원, 비낕쪽 큰 원 원형으로 분포되어 있는 데이터
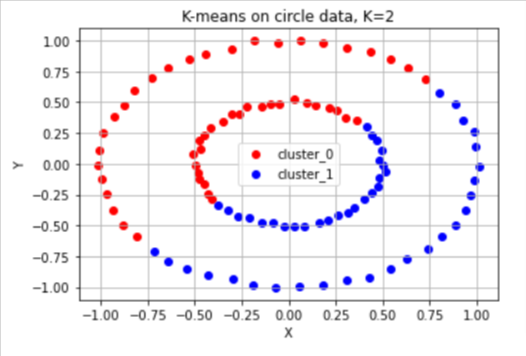
초승달 모양의 데이터
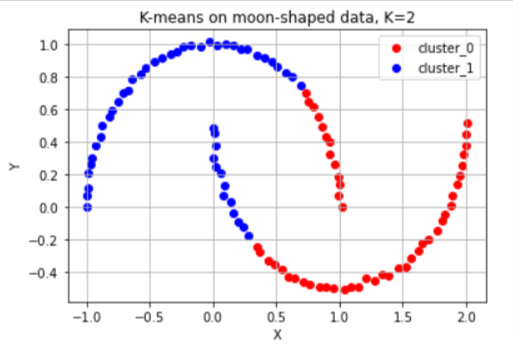
크게 3개의 대각선 방향으로 나열되어 있는 데이터

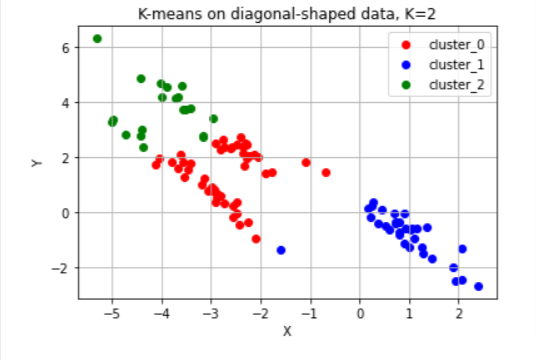
위 과정의 자세한 코드를 아래의 GitHub 링크에 기록하였다.

GitHub Link : FD17_Unsupervised_Learning

클러스터링 - DBSCAN

K-means 알고리즘을 사용하여 해결하기 어려웠던 문제들을 DBSCAN 알고리즘을 활용해 해결할 수 있다.

DBSCAN(Density Based Spatial Clustering of Applications with Noise) 알고리즘 은 가장 널리 알려진 밀도(density) 기반의 군집 알고리즘 이다.

DBSCAN 의 특징은 아래와 같다.

군집의 개수를 미리 지정할 필요가 없음
조밀하게 몰려 있는 클러스터를 군집화하는 방식을 사용 -> 원 모양의 군집이 아닌 불특정한 형태의 군집화 가능
K-means 알고리즘에 비해 훨씬 유연한 사용이 가능하기 때문에 DBSCAN은 굉장히 보편적으로 사용
단점 : 클러스터의 밀도가 다양할 때 다른 것만큼 잘 수행되지 않음

DBSCAN 를 이해하는데 필수적인 변수 및 용어는 아래 정리했다.

epsilon: 클러스터의 반경
minPts: 클러스터를 이루는 개체의 최솟값
core point: 반경 epsilon 내에 minPts 개 이상의 점이 존재하는 중심점
border point: 군집의 중심이 되지는 못하지만, 군집에 속하는 점
noise point: 군집에 포함되지 못하는 점

DBSCAN에서는 epsilon과 minPts 값을 미리 지정해 주어야 한다.

DBSAN 알고리즘

전체적인 DBSCAN 알고리즘의 순서는 다음과 같이 구성된다.

1. 임의의 점 p를 설정하고, p를 포함하여 주어진 클러스터의 반경(elipson) 안에 포함되어 있는 점들의 개수를 셈
1. 만일 해당 원에 minPts 개 이상의 점이 포함되어 있으면, 해당 점 p를 core point로 간주하고 원에 포함된 점들을 하나의 클러스터로 묶음
1. 해당 원에 minPts 개 미만의 점이 포함되어 있으면, 일단 pass
1. 모든 점에 대하여 돌아가면서 1~3 번의 과정을 반복, 만일 새로운 점 p'가 core point가 되고 이 점이 기존의 클러스터(p를 core point로 하는)에 속한다면, 두 개의 클러스터는 연결되어 있다고 하며 하나의 클러스터로 묶음
1. 모든 점에 대하여 클러스터링 과정을 끝냈는데, 어떤 점을 중심으로 하더라도 클러스터에 속하지 못하는 점이 있으면 이를 noise point로 간주. 또한, 특정 군집에는 속하지만 core point가 아닌 점들을 border point라고 칭함

K-means로는 잘되지 않았던 예시들이 DBSCAN에서는 어떻게 처리되는지 비교해보자.

가운데 작은 원, 비낕쪽 큰 원 원형으로 분포되어 있는 데이터
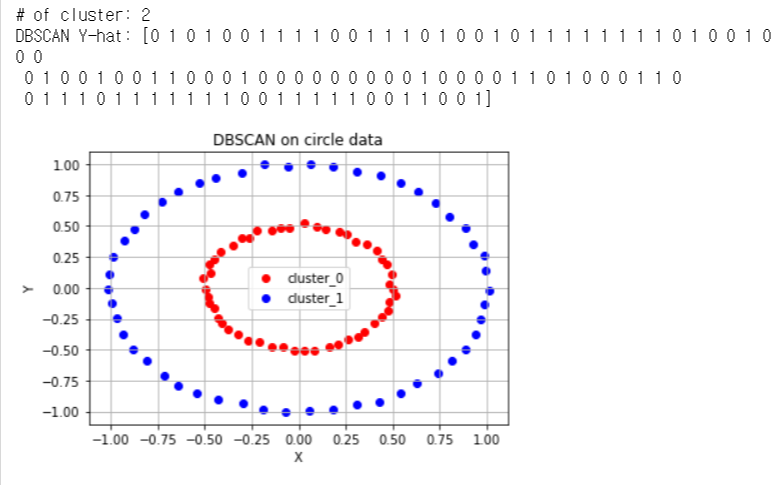
초승달 모양의 데이터
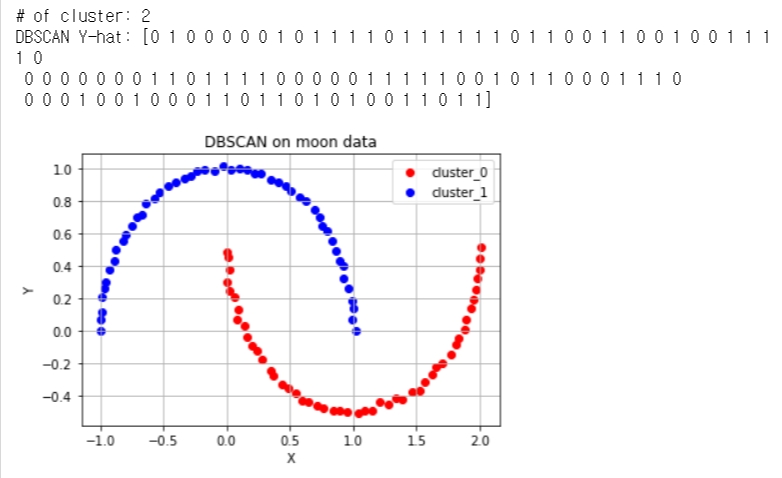
크게 3개의 대각선 방향으로 나열되어 있는 데이터

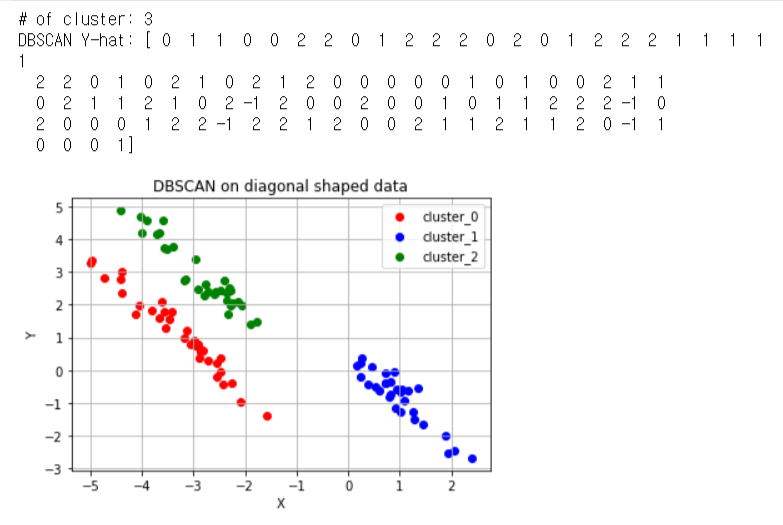
위 과정의 자세한 코드를 아래의 GitHub 링크에 기록하였다.

GitHub Link : FD17_Unsupervised_Learning

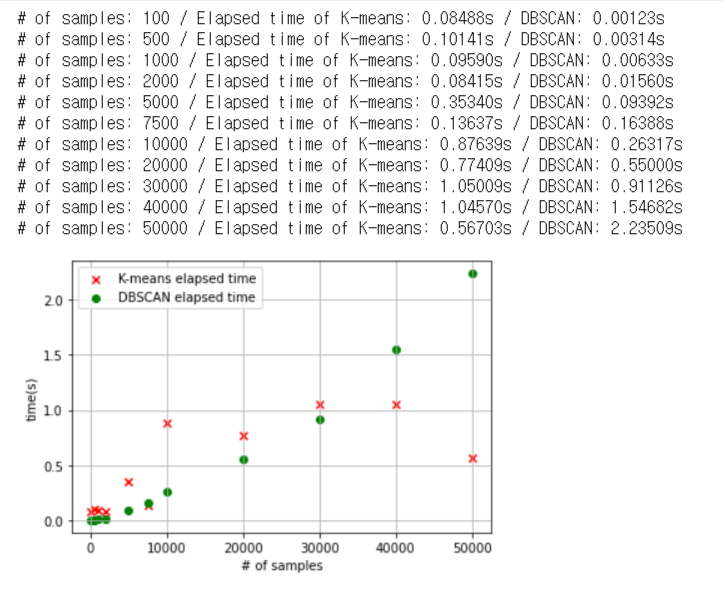
DBSCAN 알고리즘과 K-means 알고리즘의 소요 시간 비교

위 과정의 자세한 코드를 아래의 GitHub 링크에 기록하였다.

GitHub Link : FD17_Unsupervised_Learning

데이터의 수가 적을 때는 K-means 알고리즘의 수행 시간이 DBSCAN에 비해 더 김.
군집화할 데이터의 수가 많아질수록 DBSCAN의 알고리즘 수행 시간이 급격하게 늘어남.

차원 축소 - PCA

비지도학습의 대표적인 방법 중 하나로 주성분분석(PCA)이라는 차원 축소(Dimensionality reduction) 알고리즘이 있다.

차원 축소는 쉽게 말해, 우선순위를 정해서 해당 요소를 기준으로 필터링을 하고, 특정 요소는 고려하지 않는 것이다.

비지도학습에서는 데이터를 나타내는 여러 특징(feature)들 중에서 어떤 특징이 가장 그 데이터를 잘 표현(represent) 하는지 알게 해주는 특징 추출(feature extraction) 의 용도로 사용된다.

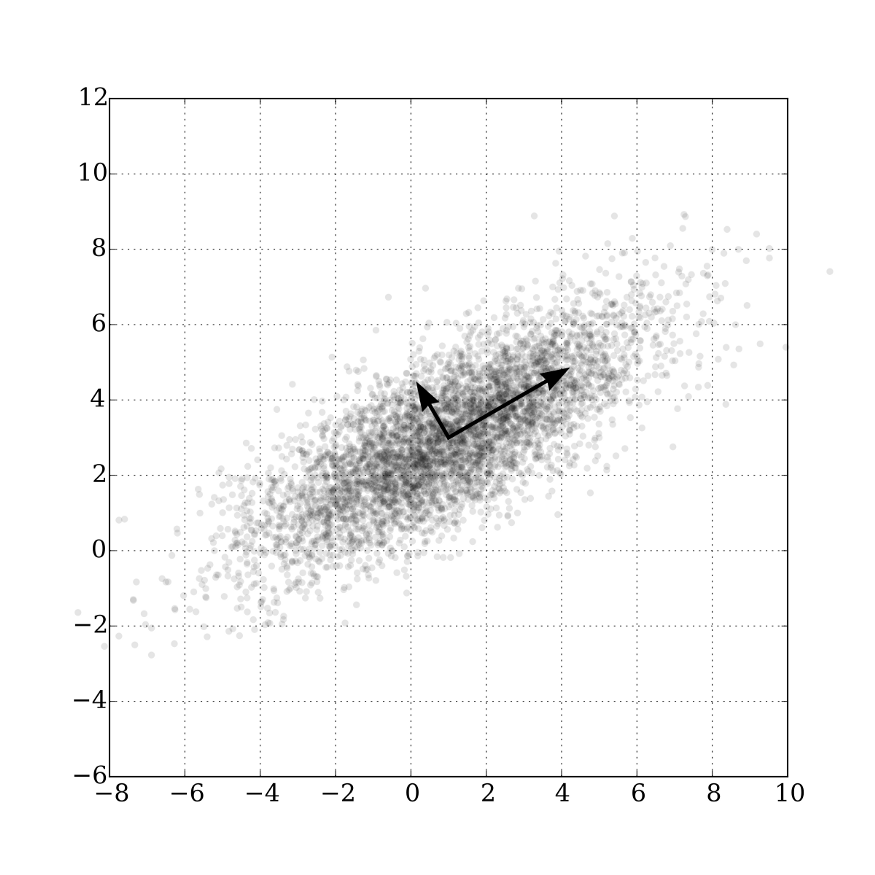
PCA는 데이터 분포의 주성분을 찾아주는 방법이다. 여기서 주성분이라는 의미는 데이터의 분산이 가장 큰 방향벡터를 의미한다.

PCA는 데이터들의 분산을 최대로 보존하면서, 서로 직교(orthogonal)하는 기저(basis, 분산이 큰 방향벡터의 축) 들을 찾아 고차원 공간을 저차원 공간으로 사영(projection) 한다.

이렇게 찾은 가장 중요한 기저를 주성분(Principal Component) 방향 , 또는 pc축 이라고 한다.

또한 PCA에서는 기존 feature 중 중요한 것을 선택하는 방식이 아닌 기존의 feature를 선형 결합(linear combination) 하는 방식을 사용한다.

PCA 예제

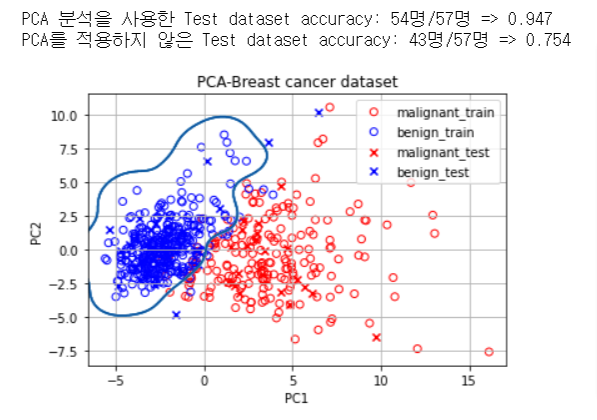
scikit-learn 을 사용해서 유방암 데이터셋에 PCA 알고리즘을 적용해보자.

위 과정의 자세한 코드를 아래의 GitHub 링크에 기록하였다.

GitHub Link : FD17_Unsupervised_Learning

단 2개의 주성분 feature 만으로 분류한 PCA classifier의 정확도가 30개의 feature를 모두 사용한 original classifier보다 훨씬 높은 분류 정확도를 보인다.

feature의 수가 적더라도, 악성/양성과 관련이 깊은 중요한 feature만을 이용한 분류의 정확도가 훨씬 더 높을 수 있다.

즉, PCA는 각 feature 간 상관관계가 있고 이를 추릴 필요가 있을 때 유용하게 사용되는 비지도학습 방법이다.

차원 축소 - T-SNE

T-SNE(T-Stochastic Neighbor Embedding) 는 시각화에 많이 쓰이는 알고리즘이다.

T-SNE를 이용하여 기존 차원의 공간에서 가까운 점들은, 차원축소된 공간에서도 여전히 가깝게 유지하게 만든다.

PCA 와 T-SNE 이 각각 주력하는 점은 다음과 같다.

PCA는 데이터가 가진 고유한 물리적 정보량을 보존하는데 주력
T-SNE는 고유한 물리적 정보량보다는 데이터들 간의 상대적 거리를 보존하는데 주력

T-SNE 예제

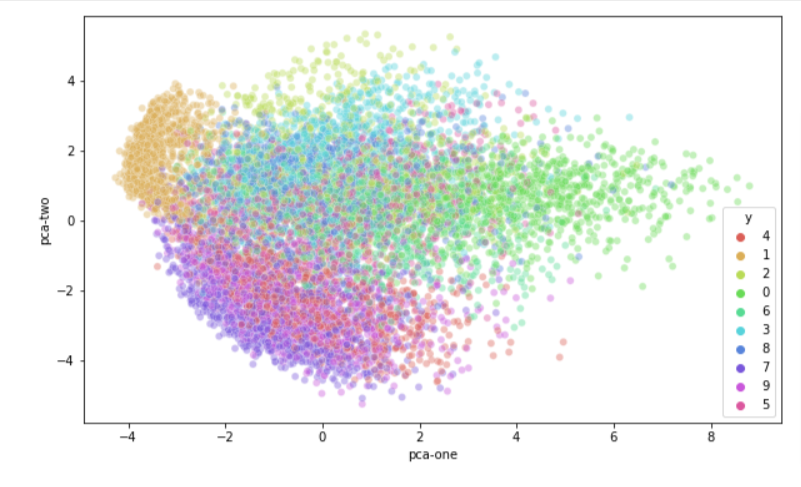
scikit-learn 제공하는 MNIST 데이터를 가져와 PCA와 T-SNE를 이용하여 차원축소를 하고 시각화를 하여 비교하였다.
PCA 를 이용한 차원 축소 시각화
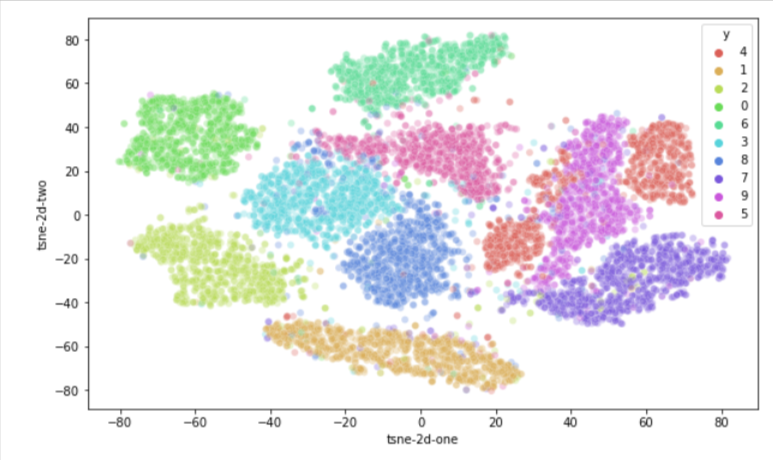
T-SNE 를 이용한 차원 축소 시각화