AIFFEL FD #23 정보이론 Information Theory

✅ 핵심내용

• Information Content
• Entropy
• Kullback Leibler Divergence
• Cross Entropy Loss
• Decision Tree와 Entropy

Information Content

정보 이론(information theory) 이란 추상적인 '정보'라는 개념을 정량화하고 정보의 저장과 통신을 연구하는 분야이다.

정보량 (Information content)

Goodfellow, Bengio, Courville의 책 Deep Learning에는 정보를 정량적으로 표현하기 위해 필요한 세 가지 조건이 설명되어있다.

• 1. 일어날 가능성이 높은 사건은 정보량이 낮고, 반드시 일어나는 사건에는 정보가 없는 것이나 마찬가지
• 2. 일어날 가능성이 낮은 사건은 정보량이 높음
• 3. 두 개의 독립적인 사건이 있을 때, 전체 정보량은 각각의 정보량을 더한 것과 같음

사건 $x$가 일어날 확률을 $P(X=x)$ 라고 할 때, 사건의 정보량(information content) $I(x)$는 다음과 같이 정의된다.

$I(x)=-\log _{b} P(x)$

(로그의 밑 $b$ 는 정보를 나타내기 위해 필요한 비트(bit)의 개수로 주로 2, $e$, 10과 같은 값이 사용된다.)

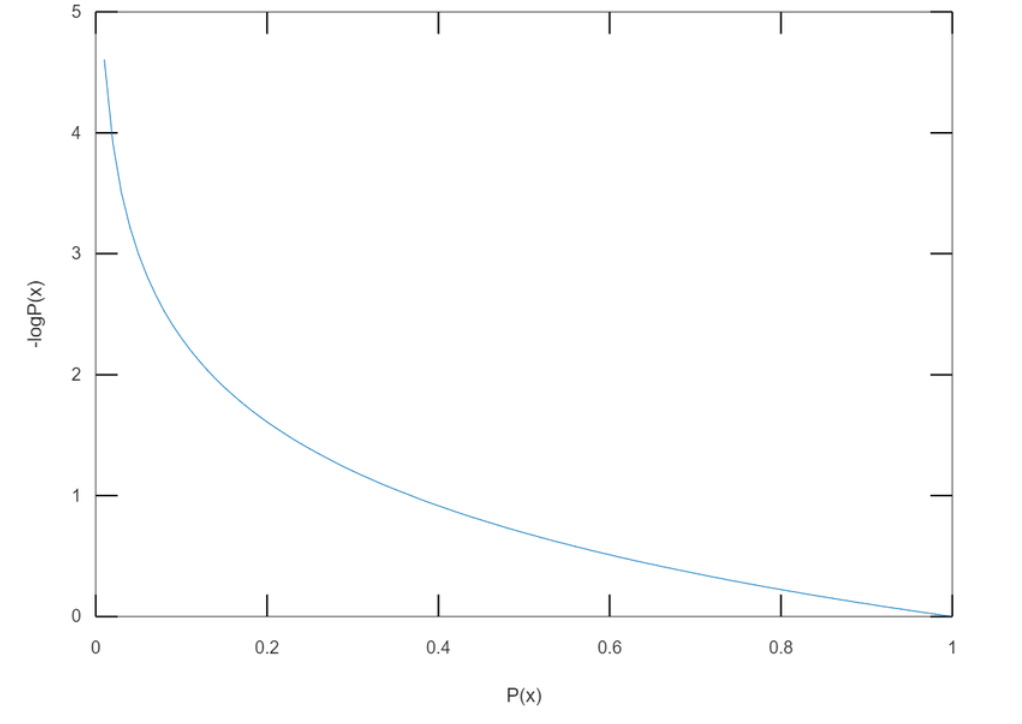
Information Content 에 대한 내용을 쉽게 이해하기 위한 간단한 예시를 아래의 GitHub 에 정리하였다.

GitHub Link :

Entropy

여러 가지 경우의 수가 존재하는 실험의 정보량도 구할 수 있을까?

직관적으로 확률 변수가 가지는 모든 경우의 수에 대해 정보량을 구하고 평균을 내면 확률 변수의 평균적인 정보량을 구할 수 있을 것이다.

특정 확률분포를 따르는 사건들의 정보량 기댓값을 엔트로피(entropy)라고 한다.

Discrete Random Variables

이산 확률 변수 $X$가 $x_{1}, x_{2}, \ldots, x_{n}$중 하나의 값을 가진다고 가정하자.
엔트로피(Entropy)는 각각의 경우의 수가 가지는 정보량에 확률을 곱한 후, 그 값을 모두 더한 값이다.

$H(X)=\mathbb{E}_{X \sim P}[I(x)]=-\sum_{i=1}^{n} p_{i} \log p_{i} \quad\left(p_{i}:=P\left(X=x_{i}\right)\right)$

엔트로피의 직관적인 개념은 무질서도 또는 불확실성 과 비슷하게 생각할 수 있다.

간단한 예시로 여러 개의 공이 들어 있는 주머니에서 공을 꺼낼 때 각각의 엔트로피 값을 계산해보았다.

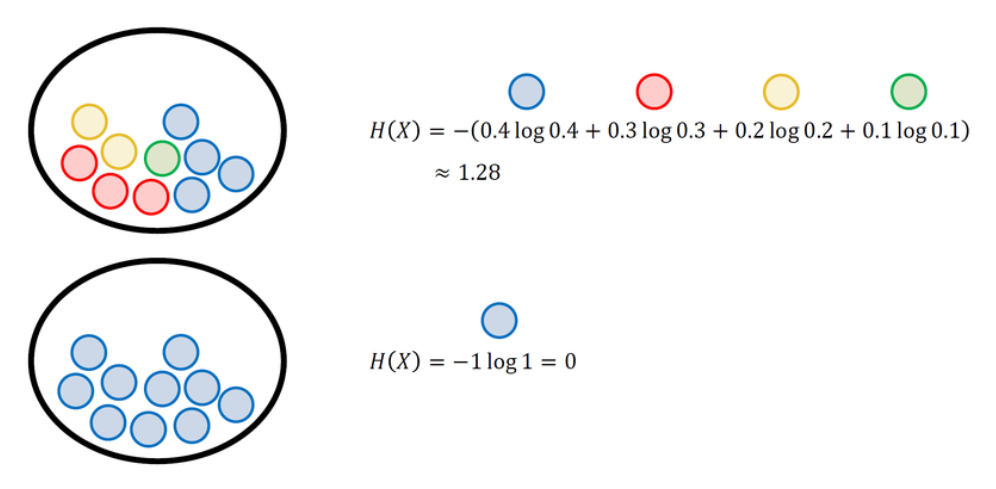
아래와 같이 확률 변수가 가질 수 있는 값의 가짓수가 같을 때(여기에서는 빨간색/파란색), 사건들의 확률이 균등할수록 엔트로피값은 증가한다. 즉, 빨간 공과 파란공이 균등하게 존재하여 결과를 예측하기가 더 어렵기 때문에 불확실성이 크다고 할 수 있다.

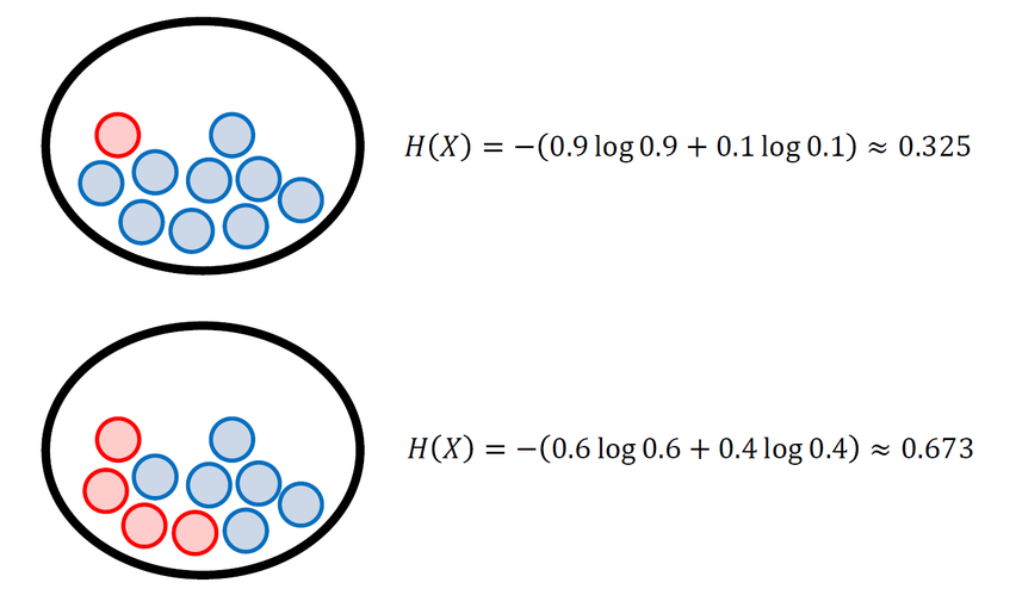
For Continuous Random Variables

$X$가 연속적인 값을 갖는 연속 확률 변수일 때는 유한합 대신 적분의 형태로 정의한다.
확률 변수 $X$의 확률 밀도 함수가 $p(x)$일 때 엔트로피는 다음과 같다.

$h(X)=-\int p(x) \log p(x) d x$

연속 확률 변수의 엔트로피를 이산 확률 변수와 구분하여 미분 엔트로피(differential entropy) 라고 부르기도 한다.

Kullback Leibler Divergence

머신러닝의 목표는 새로운 입력 데이터가 들어와도 예측이 잘 되도록, 모델의 확률 분포를 데이터의 실제 확률 분포에 가깝게 만드는 것이다.

추가예정