Dijkstra 다음은 Bellman-Ford 알고리즘이죠.
MIT 6006 강좌의 17번째 강의입니다.
개인적으로는 Dijkstra보다 원리가 훨씬 단순해서 더 이해하기 편했습니다.
구현의 경우에도 negative cycle을 체크하는 코드 정도가 추가되었을 뿐 Dijkstra의 경우보다 짧아졌습니다.
덕분에 대부분의 코드를 Dijkstra에서 가져와서 재활용(?)했습니다.
Dijkstra와 비교해서 Bellman-Ford 알고리즘은 negative weight를 가진 경우에도 경로를 구할 수 있지만 negative cycle이 있는 경우에는 경로를 구할 수 없습니다.
즉,
✅ Negative weights
✅ Positive weights(+ positive cycle)
❌ Negative cycle
의 관계가 성립합니다.
아래는 코드 실행 결과입니다.
첫번째는 negative cycle이 있는 경우입니다.
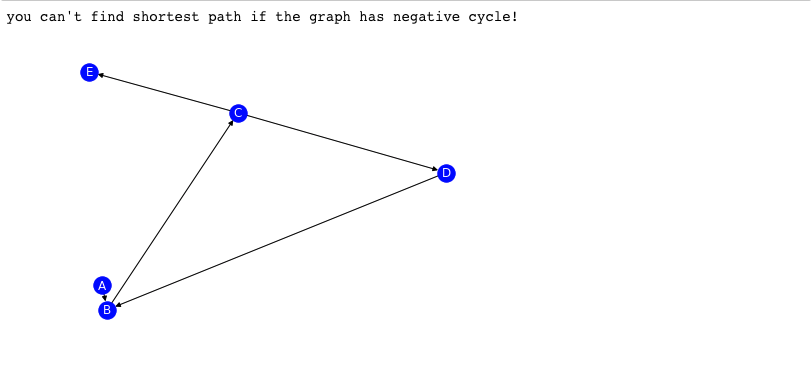
그래프에는 weight이 보이지 않지만, 'B', 'C', 'D' 사이에 negative cycle이 있고, 이를 체크하여 에러메시지를 보여줍니다.
다음은 Dijkstra에서 이미 다루었던 Positive weights 그래프입니다. 보시다시피 제대로 경로를 찾아냅니다. Bellman-Ford 알고리즘은 여기에 일부 경로가 Negative weights를 가지더라도 경로를 찾아낼 수 있습니다.
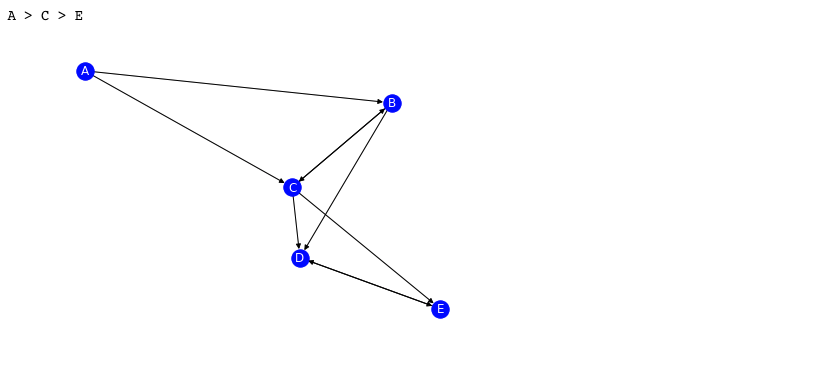
아래는 코드 샘플입니다.
# Bellman-Ford implementation from MIT 6006 course lesson #17
import math
import networkx as nx
# utility: Graph
class Graph:
def __init__(self, vertices):
self.V = vertices
self.edges = []
def add_edge(self, edge):
self.edges.append(edge)
def __str__(self):
result = ''
for edge in self.edges:
result += f'{v}: {str(edge)}, \n'
return result
def bellmanFord(graph, s):
"""
Idea behind bellman-ford vs dijkstra:
They both can be used to find shortest path. But their approach is different.
Dijkstra is a greedy algorithm, which means it makes 'best optimal answer' for each given step.
But it fails when it encounters negative weights. Why? Because you can improve the weight by adding
one more iteration of relaxing all the edges.
However, Bellman-Ford is not a greedy algorithm. It just inspects for all the possible improvements
simply by looping over edges |V| - 1 times to get the best weight for 'shortest simple path'(SSP).
Then why |V| - 1 times? The length of the longest simple path(path w/o cycle) would be |V| - 1.
For example, you need 2 edges to connect 3 vertices, otherwise, there exists a negative cycle.
"""
d = dict.fromkeys(graph.V, math.inf) # distance pair
# will have default value of Infinity
pi = dict.fromkeys(graph.V, None) # map of parent vertex
# initialize
d[s] = 0
def relax(u, v, w):
if d[v] > d[u] + w:
d[v] = d[u] + w
pi[v] = u
# The length of the longest simple path(path w/o cycle) would be |V| - 1.
# For example, you need 2 edges to connect 3 vertices.
# Otherwise, there exists a negative cycle.
for i in graph.V[:-1]:
for u, v, w in graph.edges:
relax(u, v, w)
for u, v, w in graph.edges:
# even after relaxing all the edges for |V| - 1 times,
# we still have the posibillity to improve the existing path
# this means there are negative cycles
if d[v] > d[u] + w:
return f'there exists a negetive cycle!'
return d, pi
def shortest_path(s, t):
try:
d, pi = bellmanFord(g, s)
except ValueError:
return 'you can\'t find shortest path if the graph has negative cycle!'
path = [t]
current = t
# if parent pointer is None,
# then it's the source vertex
while pi[current]:
path.insert(0, pi[current])
# set current to parent
current = pi[current]
if s not in path:
return f'unable to find shortest path staring from "{s}" to "{t}"'
return f'{" > ".join(path)}'
g = Graph(['A', 'B', 'C', 'D', 'E'])
# graph with negative cycle
nc_edges = [('A', 'B', 5), ('B', 'C', -1), ('C', 'D', 2), ('D', 'B', -2), ('C', 'E', 4)]
# w/o negative cycles
edges = [\
('A', 'B', 10), ('A', 'C', 3), ('B', 'C', 1), ('C', 'B', 4), \
('B', 'D', 2), ('C', 'D', 8), ('D', 'E', 7), ('E', 'D', 9), ('C', 'E', 2)]
# used for both finding shortest path and drawing graph
current_edge_group = edges
for edge in current_edge_group:
g.add_edge(edge)
print( shortest_path('A', 'E') )
G = nx.DiGraph()
G.add_weighted_edges_from(current_edge_group)
nx.draw(G, with_labels = True, node_color='b', font_color='w')코드에 대한 지적은 언제나 환영합니다. 감사합니다. 😀
