MIT의 6006 #16을 듣고 정리한 코드입니다.
파이썬의 heapq 모듈을 이용해서 직접 priority queue를 구현해서 사용했고,
그래프를 그리기 위해 networkx 모듈을 사용했습니다. (코드를 돌려보시려면 설치하셔야 됩니다!)
강의는 링크에서 들으실 수 있습니다.
코드에 대한 피드백은 언제나 환영합니다 😀
# dijkstra implementation from MIT 6006 course lesson #16
from collections import defaultdict
import math
from heapq import heapify, heappush, heappop
import networkx as nx
# utility: priority queue
class Pq:
def __init__(self):
self.queue = []
def __str__(self):
return str(self.queue)
def insert(self, item):
heappush(self.queue, item)
def extract_min(self):
return heappop(self.queue)[1]
def update_priority(self, key, priority):
for v in self.queue:
if v[1] == key:
v[0] = priority
heapify(self.queue)
def empty(self):
return len(self.queue) == 0
# utility: Graph
class Graph:
def __init__(self, vertices):
self.V = vertices
self.graph = defaultdict(lambda: [])
def add_edge(self, v, u, w):
self.graph[v].append((u, w))
def __str__(self):
result = ''
for v in self.V:
result += f'{v}: {str(self.graph[v])}, \n'
return result
def dijkstra(graph, s):
Q = Pq() # priority queue of vertices
# [ [distance, vertex], ... ]
d = dict.fromkeys(graph.V, math.inf) # distance pair
# will have default value of Infinity
pi = dict.fromkeys(graph.V, None) # map of parent vertex
# useful for finding shortest path
# initialize
d[s] = 0
# update priority if prior path has larger distance
def relax(u, v, w):
if d[v] > d[u] + w:
d[v] = d[u] + w
Q.update_priority(v, d[v])
pi[v] = u
# initialize queue
for v in graph.V:
Q.insert([d[v], v])
while not Q.empty():
u = Q.extract_min()
for v, w in graph.graph[u]:
relax(u, v, w)
return d, pi
def shortest_path(s, t):
d, pi = dijkstra(g, s)
path = [t]
current = t
# if parent pointer is None,
# then it's the source vertex
while pi[current]:
path.insert(0, pi[current])
# set current to parent
current = pi[current]
if s not in path:
return f'unable to find shortest path staring from "{s}" to "{t}"'
return f'{" > ".join(path)}'
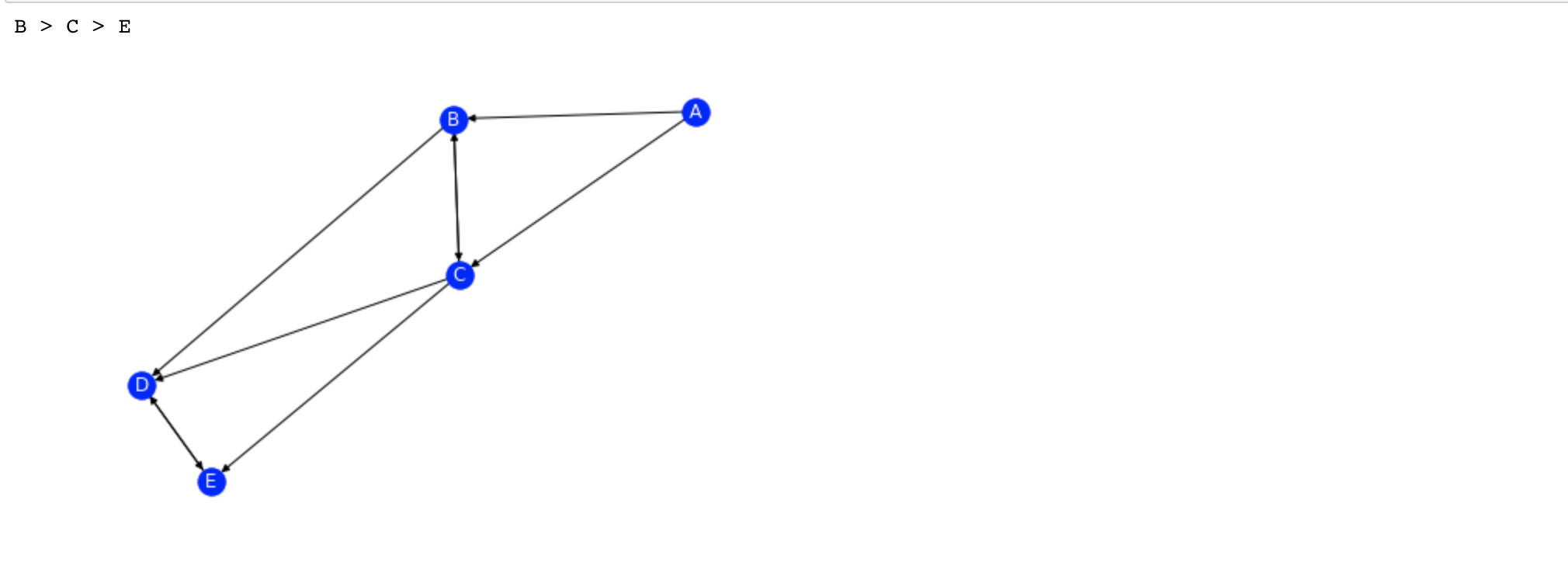
g = Graph(['A', 'B', 'C', 'D', 'E'])
g.add_edge('A', 'B', 10)
g.add_edge('A', 'C', 3)
g.add_edge('B', 'C', 1)
g.add_edge('C', 'B', 4)
g.add_edge('B', 'D', 2)
g.add_edge('C', 'D', 8)
g.add_edge('D', 'E', 7)
g.add_edge('E', 'D', 9)
g.add_edge('C', 'E', 2)
print( shortest_path('B', 'E') )
G = nx.DiGraph()
G.add_weighted_edges_from([\
('A', 'B', 10), ('A', 'C', 3), ('B', 'C', 1), ('C', 'B', 4), \
('B', 'D', 2), ('C', 'D', 8), ('D', 'E', 7), ('E', 'D', 9), ('C', 'E', 2)])
nx.draw(G, with_labels = True, node_color='b', font_color='w')<코드 실행결과>


덕분에 다익스크라 알고리즘을 확실하게 이해했습니다!!
이 코드의 시간 복잡도는 어떻게 되는건가요???