1. Ranking Instead of Classifying

일반적으로 분류(Classification) 모델은 특정 임계치(threshold)를 기준으로 예측값을 양분합니다. 그러나 실제 비즈니스 상황에서는 "어떤 사례는 거의 확실히 긍정 클래스이고, 어떤 사례는 긍정일 가능성이 낮다"와 같이 확률적 점수나 스코어를 통해 순위를 매길 수 있습니다.

이렇게 순위(Ranking)만 있어도, 가장 가능성이 높은 사례부터 우선적으로 목표 행동을 취하거나 자원을 할당할 수 있으므로, 정확한 확률을 모를 때도 의사결정에 유용합니다.

예를 들어, 마케팅 캠페인 시 고객에게 오퍼를 보낼 때, 정확히 “이 고객이 반응할 확률이 15%인지 20%인지” 모르더라도, “이 고객이 다른 고객보다 더 높은 반응 가능성을 가진다”는 순위 정보만으로도 효율적인 전략 수립이 가능합니다.

• If one is going to target the highest expected value cases using costs and benefits that are constant for each class, then ranking cases by likelihood of the target class is sufficient

왜 순위만 있어도 충분한가?

마케팅 예시로 말해보겠습니다.

어떤 회사가 신규 제품을 홍보하기 위해 마케팅 캠페인을 진행하려고 합니다.
캠페인 대상 고객에게 우편 광고를 보내는 데에는 건당 1달러의 비용이 들고, 반응(구매)이 일어날 경우 5달러의 이익이 발생한다고 가정합니다.
고객 DB에 1,000명의 후보가 있고, 각 고객이 반응할 확률을 예측할 수 있는 (혹은 점수를 매길 수 있는) 모델이 있습니다.

두 가지 접근 방법

분류(Classification) 모델

모델이 고객별로 “반응/비반응”을 확정적으로 분류하고, 특정 임계치(예: 반응 확률이 0.5 이상이면 ‘반응’, 미만이면 ‘비반응’)를 사용합니다.
이렇게 되면 0.49와 0.51 사이에 있는 고객 두 명은 사실상 확률이 큰 차이가 없어도, 한 명은 캠페인 대상(반응으로 분류), 한 명은 비대상(비반응으로 분류)이 됩니다.

랭킹(Ranking) 기반 접근

모델이 각 고객마다 0~1 사이의 점수를 매겨 “반응 가능성” 순위로 고객을 정렬합니다.
예컨대 A 고객: 0.85, B 고객: 0.40, C 고객: 0.70 등으로 점수가 매겨지면,
정확히 0.85가 실제로 0.85인지, 0.80인지, 0.90인지는 몰라도 “A가 B보다 구매 가능성이 높다”는 것은 알 수 있습니다.
예산이 한정되어 있거나, 가장 반응률이 높은 상위 200명만을 공략하고 싶을 때, 점수가 높은 순으로 200명을 추려서 마케팅을 진행합니다.
0.85 > 0.70 > 0.40 순으로 우선순위를 두어 A, C, B 고객 순으로 대상 여부를 결정.
이 때, 반응 확률의 “정확한 값”보다는 누가 더 높고 낮은지에 대한 랭킹 정보가 효율적인 의사결정을 가능하게 합니다.

왜 랭킹만으로 충분한가?

비용과 편익이 클래스별로 일정하다면(예: “광고 우편 비용은 건당 1달러, 구매 시 이익은 5달러”), 가장 높은 기대값을 주는 고객(즉, 반응 확률이 상대적으로 높은 고객)부터 공략하는 전략이 합리적입니다.
이때, 확률이 15%인지 20%인지가 아주 정확하지 않아도 “A가 B보다 더 높은 확률로 구매할 것이다”라는 정보만으로 “A를 B보다 먼저 공략”하면 됩니다.
결과적으로 상위 랭킹에 있는 고객부터 차례대로 마케팅 예산을 투입하여, 반응률(ROI)을 극대화할 수 있습니다

The Confusion Matrix

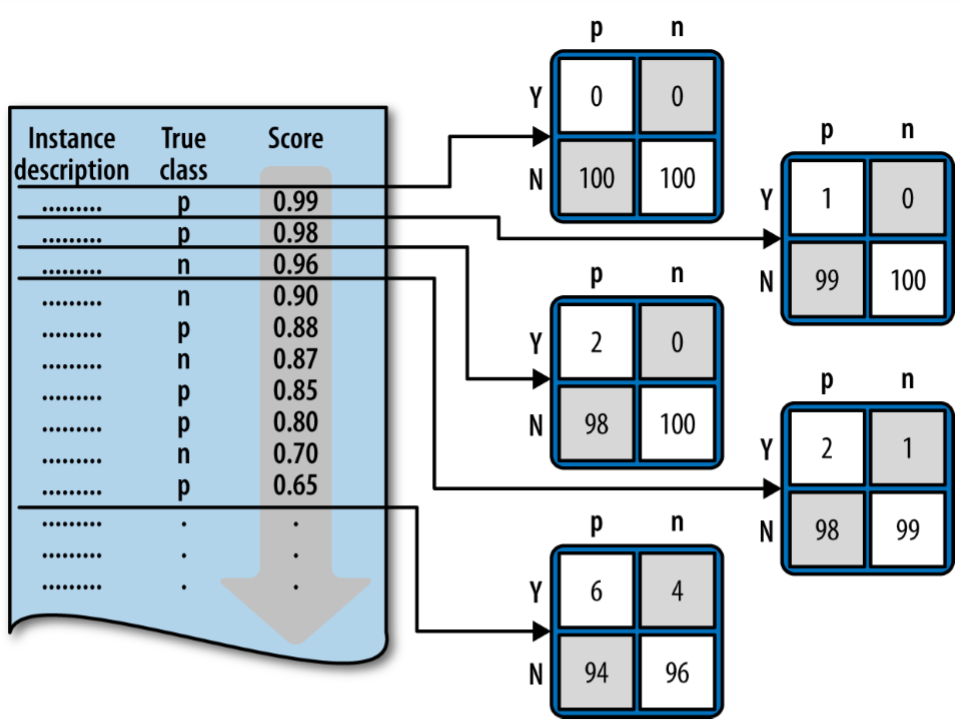
Whenever the threshold changes, the confusion matrix may change as well because the numbers of true positive and false positive change.

As the threshold is lowered, instances move up from the N row into Y row of the confusion matrix.• If the instance was a positive (in the “p” column) it moves up and becomes a true positive (Y,p). If it was a negative (n), it becomes a false positive(Y,n).
즉, 임계치 위는 positive, 아래는 negative

---

2. Profit Curves(수익곡선)

수익곡선(Profit Curves)은 모델의 예측에 따른 기대 이익(또는 손실)을 그래프로 표현한 것입니다.

• 모델이 고객을 긍정(반응)으로 예측할 때마다 비용과 이익을 계산하면, 임계치에 따라 얻을 수 있는 총 기대 이익이 달라집니다.

• 임계치를 조정하면서 각 시점에서의 기대 이익을 계산해 그래프로 표현하면, 모델이 어디에서 최대 이익을 내는지, 혹은 어떤 부분에서 비용이 발생하는지 한눈에 파악할 수 있습니다.

• 사전확률(클래스 비율)과 비용/이익 구조가 명확히 주어졌을 때 유용하게 사용할 수 있습니다.

As we move down the threshold “down” the ranking, we get additional instances predicted as being positive rather than negative

With a ranking classifier, we can produce a list of instances and their predicted scores, ranked by decreasing score, and then measure the expected profit that would result from choosing each successive cut-point in the list.

At each cut-point we record the percentage of the list predicted as positive and the corresponding estimated profit. (각 cut point에 해당하는 수익을 계산) Graphing these values gives us a profit curve

Profit Curves for Three Classifier

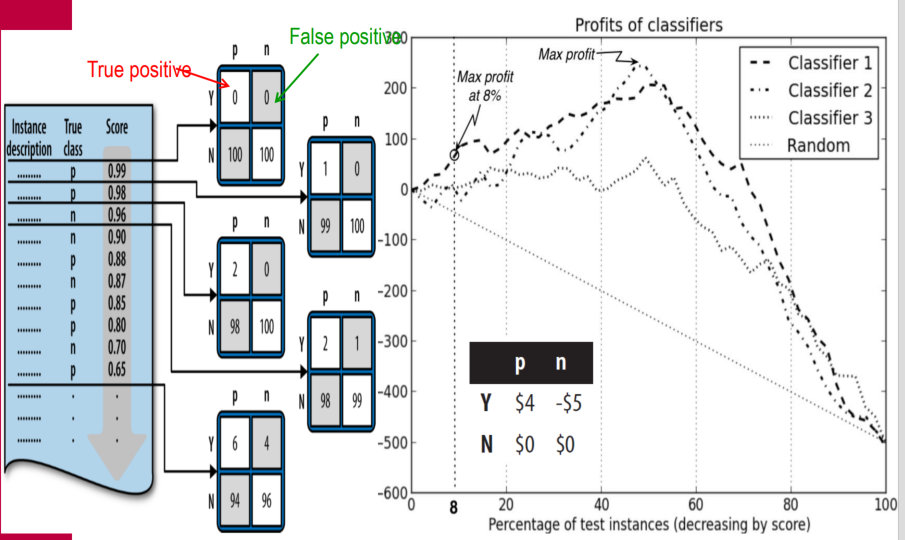
The curve show that profit can go negative when the profit margin is thin and the number of responders is small. Making offers too many people who won’t respond.(비용과다로 손실 발생)

When no customers are targeted there are no expenses and zero profit: when everyone is targeted, every classifier performs the same..

Classifier 2 produces the maximum profit of $200 by targeting the top-ranked 50% of customers

---

3. ROC Graphs and Curves

ROC(Receiver Operating Characteristic) 그래프는 모델의 True Positive Rate(TPR)(TPR = TP / P)와 False Positive Rate(FPR)(FPR = FP / N)를 서로 다른 임계치에 대해 플로팅한 그래프입니다.

• ROC 그래프는 모델의 분류 성능을 클래스의 비율이나 비용/이익에 독립적으로 평가할 수 있게 해줍니다.
• 임계치를 변화시키면 TPR과 FPR이 변하고, 이를 곡선으로 나타낸 것이 ROC 커브입니다.
• ROC 커브의 왼쪽 상단 방향에 위치할수록 높은 성능을 의미합니다. 대각선은 무작위 추측(random guessing)을 의미하고, 대각선 위에 위치하는 모델은 무작위보다 나은 성능을 보여줍니다.

If both class priors and cost-benefit estimates are known and are expected to be stable, profit curves may be a good choice for visualizing model performance (사전 확률과 비용/이익을 미리 알 수 있을 때 수익곡선 사용 가능)

One approach to handling uncertain condition is the Receiver Operating Characteristics (ROC) graph (이들 값이 불확실할 경우 ROC 그래프 사용, 수신자 운용 특성)

ROC Graph

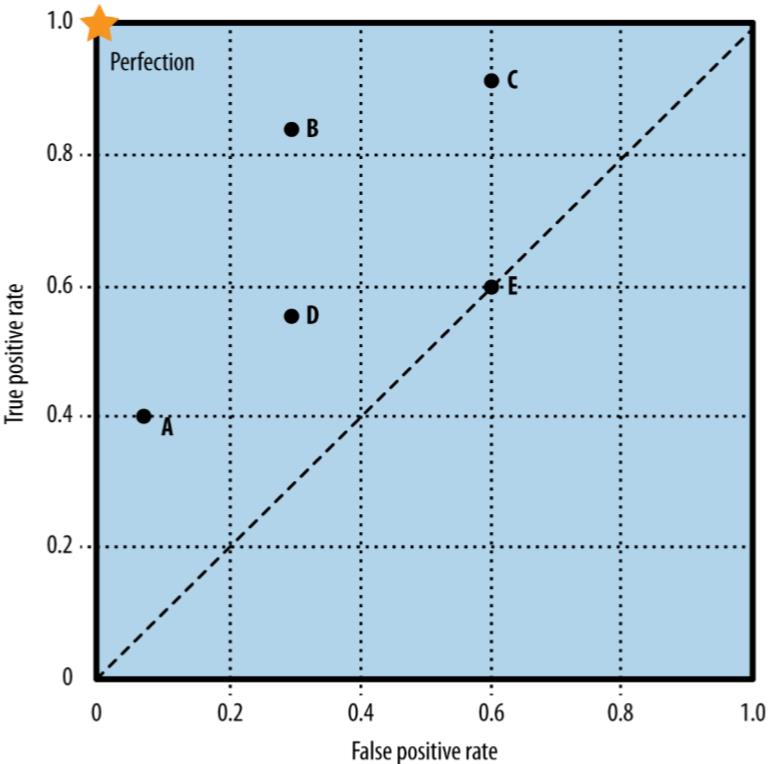
• A ROC graph is a two dimensional plot of a classifier with false positive rate on the x axis against true positive rate on the y axis.
• A ROC graph depicts relative trade-offs that a classifier makes between benefits(true positive) and costs(false positive
• Each classifier produces a confusion matrix.

The diagonal line connecting (0,0) to (1,1) represents the policy of guessing a class

Note that no classifier should be in the lower right triangle of a ROC graph. This represents performance that is worse than random guessing. (대각선 아래는 임의 분류보다 못함)

ROC 그래프에서 대각선은 랜덤 추측 수준의 성능을 의미하고, 왼쪽-아래쪽에 있을수록 보수적(conservative)이며 양성 판정을 매우 신중하게(they make positive classifications only with strong evidence),

• (0,0) 쪽 = 극도로 높은 임계치로 인해 “양성”이라고 판단하기 매우 까다로운 상태 (보수적)

오른쪽-위쪽으로 갈수록 관대하게(permissive) 양성을 남발하는 경향을 반영(they make positive classifications only with weak evidence )한다.

• (1,1) 쪽 = 극도로 낮은 임계치로 인해 대부분을 “양성”으로 분류하는 상태 (관대)

Figure 8-4 ROC Graph and Confusion Matrix

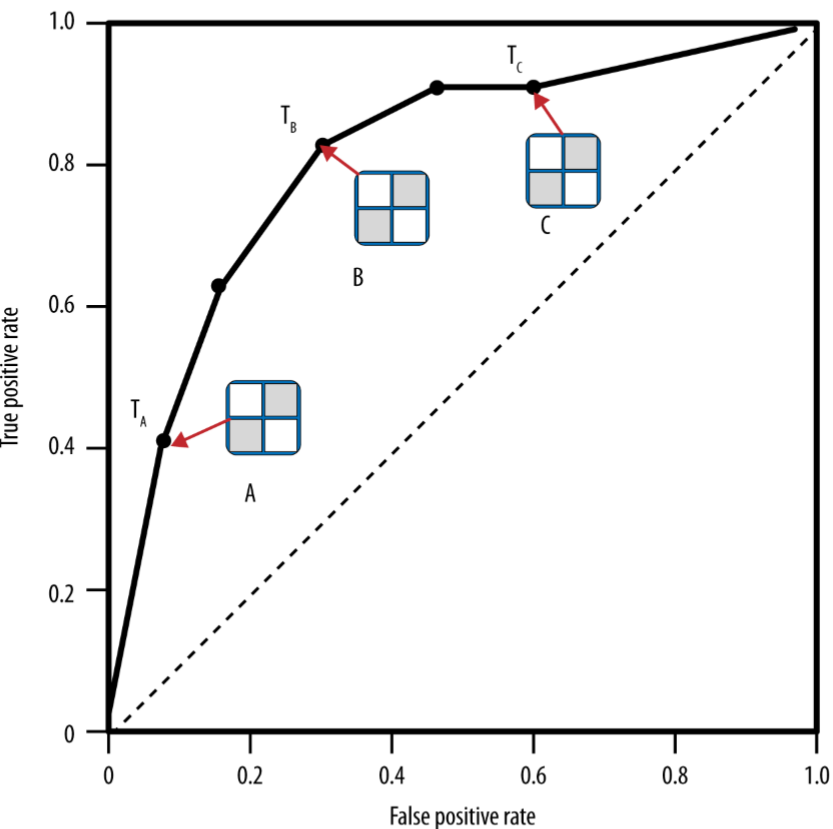
A ranking model can be used with a threshold to produce a discrete (binary) classifier: if the classifier output is above the threshold, the classifier produces a Y, else an N.

Each threshold value produces a different point in ROC space

Conceptually, we may imagine sorting the instances by score and varying a threshold from -∞ to +∞ while tracing a curve through ROC space
(개념적으로, 인스턴스들을 모델 점수에 따라 정렬한 뒤 임계치를 -∞에서 +∞ 방향으로 서서히 변화시킨다고 상상해보면, ROC 공간 위를 쭉 따라가는 곡선을 그릴 수 있다)

Sample ROC Curve

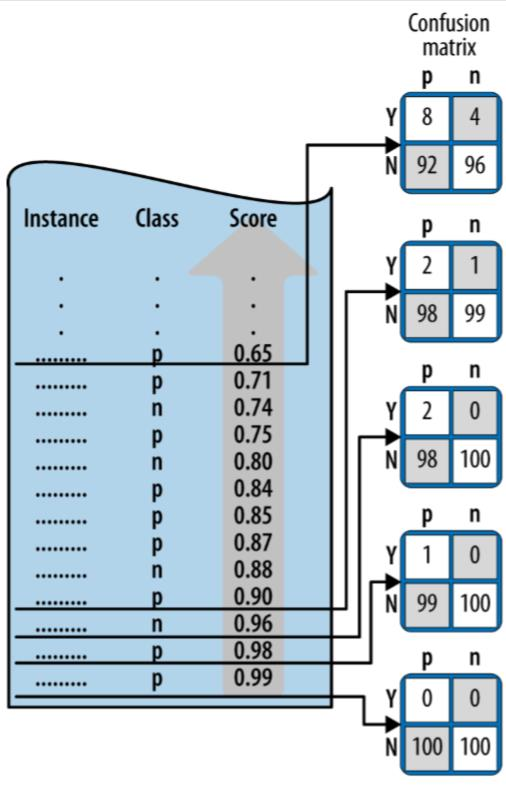
The model assigns a score to each instance and the instances are ordered decreasing from bottom to top.

• To construct the curve, start at the bottom with an initial confusion matrix where everything is classified as N.
• Moving upward, every instance moves a count of 1 from N row to the Y row, resulting in a new confusion matrix.
• Each confusion matrix maps to a (fprate, tp rate) pair in ROC space

Sample ROC Curve(2)

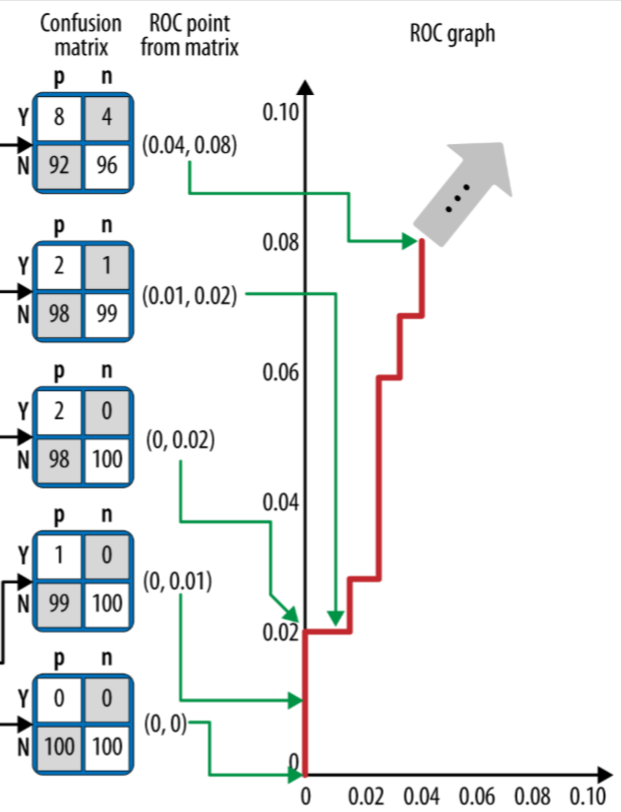
Whenever we pass a positive instance, we take a step upward (increasing true positives); whenever we pass a negative instance, we take a step rightward (increasing false positives).

• An advantage of ROC graphs is that they are independent of the class proportions as well as the costs and benefits.
• A data scientist can plot the performance of classifiers on a ROC graph.
• The region(s) on the ROC graph that are of interest may changes as costs, benefits, and class proportions change, but the curves themselves should not.

Why are ROC graphs independent of class proportions and cost/benefit?

1. ROC 곡선은 TPR(민감도)과 FPR(1 - 특이도)을 축으로 사용

• TPR (True Positive Rate): $ \frac{TP}{TP + FN}$
  • 실제 양성(Positive) 중에서 얼마나 양성으로 예측했는지를 나타내는 비율
• FPR (False Positive Rate): $\frac{FP}{FP + TN}$
  • 실제 음성(Negative) 중에서 얼마나 양성으로 잘못 예측했는지를 나타내는 비율

위 두 값은 확률(비율) 이기 때문에, 데이터셋 안에서 양성/음성 클래스를 몇 개나 가지고 있는지(클래스 비율) 와 무관하게 계산됩니다.

• 예를 들어, 실제 데이터에서 양성 사례가 10건인지, 10,000건인지 간에, TPR은 “양성 중에서 몇 %나 정확히 양성으로 예측했는가?” 만을 보여줍니다.
• 마찬가지로, 음성 사례가 10건인지 10,000건인지에 관계없이 FPR은 “음성 중에서 몇 %나 잘못된 양성으로 예측했는가?” 만을 보여줍니다.

이렇게 ROC 곡선은 절대 건수(Count)가 아니라 비율로 평가하기 때문에, 클래스 불균형이 심한 경우에도 크게 흔들리지 않습니다.

2. ROC 곡선은 비용(cost)이나 편익(benefit)을 고려하지 않는다

• ROC 곡선은 모델이 특정 판단 임계값(Threshold) 을 달리 했을 때의 TPR과 FPR를 단순히 나열하며, 이를 “민감도 vs (1 - 특이도)” 형태의 그래프로 그린 것에 불과합니다.
• 다시 말해, 양성을 음성으로 잘못 분류했을 때의 비용(혹은 손실)과 음성을 양성으로 잘못 분류했을 때의 비용의 차이가 ROC 곡선 자체에는 반영되지 않습니다.

때문에, 모델의 예측이 잘못되었을 때 들어가는 비용이나, 모델이 양성을 정확히 맞힐 때 얻을 수 있는 편익 등은 ROC 곡선에 직접적으로 영향을 미치지 않습니다.

결론

1. 클래스 비율에 독립적: ROC 곡선은 TPR과 FPR라는 비율 개념을 사용하므로, 데이터에 존재하는 양성/음성 클래스의 절대 개수 분포에 영향을 받지 않습니다.
2. 비용·편익 미반영: ROC 곡선은 기본적으로 정분류/오분류 비용을 고려하지 않고, 단순히 모델의 민감도와 특이도의 관계만 시각화합니다.

이러한 이유로, ROC 그래프는 모델의 성능을 클래스 불균형이나 비용/편익 구조에 구애받지 않고 살펴볼 수 있다는 장점이 있습니다.

---

ROC example 구체적으로 그려보자.

아래 예시는 스팸 이메일 분류 모델을 간단히 가정하고, ROC 곡선을 어떻게 그리는지 단계별로 살펴보는 방식으로 설명해 보겠습니다.

1. 예시 상황 설정

• 이메일 10개가 있다. 실제로는 그중 4개가 스팸(Positive 클래스), 6개는 스팸이 아님(Negative 클래스)이라고 하자.
• 어떤 분류 모델이 이 10개 이메일 각각에 대해 “스팸일 확률”을 예측했다고 가정해 보겠습니다.

모델의 예측 확률 (가상의 예시)

이메일	실제 라벨	예측 확률(스팸일 확률)
E1	스팸(+)	0.90
E2	스팸(+)	0.80
E3	스팸(+)	0.60
E4	스팸(+)	0.55
E5	정상(-)	0.50
E6	정상(-)	0.30
E7	정상(-)	0.20
E8	정상(-)	0.10
E9	정상(-)	0.05
E10	정상(-)	0.05

• Positive(스팸) = 4개 (E1, E2, E3, E4)
• Negative(정상) = 6개 (E5 ~ E10)

---

2. 다양한 임계값(Threshold)에 따른 TPR, FPR 계산

ROC 곡선을 그리려면, 임계값(threshold)을 다양하게 바꾸어가며 각 임계값에서의 TPR, FPR을 구해야 합니다.

• TPR(민감도, Recall) = $\displaystyle \frac{TP}{TP + FN}$
• FPR = $\displaystyle \frac{FP}{FP + TN}$

아래에서는 모델 예측 확률을 기준으로, Threshold(임계값)을 1.0부터 0.0까지 여러 구간으로 낮춰보면서 각 지점에서의 (TPR, FPR)을 구해보겠습니다.

(1) Threshold = 1.00

• 기준: “예측 확률이 1.00 이상이면 스팸으로 분류”

• 실제로 1.00 이상인 이메일은 없음

  • 예측 Positive(스팸) = 0개
  • 예측 Negative(정상) = 모든 이메일(10개)

• Confusion Matrix:

  • TP = 0 (실제 스팸을 하나도 Positive로 잡지 못함)
  • TN = 6 (실제 정상 6개를 Negative로 맞춤)
  • FP = 0 (실제 정상인데 스팸으로 오분류한 것 없음)
  • FN = 4 (스팸 4개를 모두 놓침)

• TPR = 0 / (0+4) = 0.0

• FPR = 0 / (0+6) = 0.0

→ ROC 상에서 점: (FPR=0.0, TPR=0.0)

(2) Threshold = 0.80

• 기준: “예측 확률이 0.80 이상이면 스팸으로 분류”

• 해당되는 이메일: E1(0.90), E2(0.80)

  • 예측 Positive = E1, E2
  • 예측 Negative = E3, E4, E5, E6, E7, E8, E9, E10

• Confusion Matrix:

  • TP = 2 (E1, E2: 실제 스팸 맞음)
  • TN = 6 (E5 ~ E10: 실제 정상 모두 Negative로 예측)
  • FP = 0 (정상인데 스팸으로 잘못 예측한 것 없음)
  • FN = 2 (E3, E4: 실제 스팸이지만 Negative로 예측)

• TPR = 2 / (2+2) = 0.5

• FPR = 0 / (0+6) = 0.0

→ ROC 상에서 점: (FPR=0.0, TPR=0.5)

(3) Threshold = 0.55

• 기준: “예측 확률이 0.55 이상이면 스팸으로 분류”

• 해당되는 이메일: E1(0.90), E2(0.80), E3(0.60), E4(0.55)

  • 예측 Positive = E1, E2, E3, E4
  • 예측 Negative = E5, E6, E7, E8, E9, E10

• Confusion Matrix:

  • TP = 4 (E1, E2, E3, E4: 실제 스팸 4개 전부 잡음)
  • TN = 6 (E5 ~ E10: 실제 정상 6개 모두 Negative로 맞음)
  • FP = 0 (정상인데 스팸으로 잘못 예측한 것 없음)
  • FN = 0 (스팸인데 놓친 게 없음)

• TPR = 4 / (4+0) = 1.0

• FPR = 0 / (0+6) = 0.0

→ ROC 상에서 점: (FPR=0.0, TPR=1.0)

(이 상태에선 스팸을 100% 맞추고, 정상을 100% 맞추는 드문 완벽 분류 사례가 되어버렸네요. 실제론 이렇게 깔끔하게 나오진 않겠지만, 예시로 보면 됩니다.)

(4) Threshold = 0.30

• 기준: “예측 확률이 0.30 이상이면 스팸으로 분류”

• 해당되는 이메일: E1(0.90), E2(0.80), E3(0.60), E4(0.55), E5(0.50), E6(0.30)

  • 예측 Positive = E1, E2, E3, E4, E5, E6
  • 예측 Negative = E7, E8, E9, E10

• Confusion Matrix:

  • 스팸(실제 Positive) 4개 중 → (E1, E2, E3, E4) 모두 Positive로 예측 (TP=4, FN=0)
  • 정상(실제 Negative) 6개 중 → E5(0.50), E6(0.30)는 Positive로 잘못 예측하였으므로 FP=2
    나머지 E7, E8, E9, E10 은 Negative로 맞춤(TN=4)

• TPR = 4 / (4+0) = 1.0

• FPR = 2 / (2+4) = 0.3333...

→ ROC 상에서 점: (FPR=0.33, TPR=1.0)

(5) Threshold = 0.00

• 기준: “예측 확률이 0.00 이상이면 스팸으로 분류”

  • 모든 이메일이 Positive로 예측됨

• Confusion Matrix:

  • 스팸(4) → 전부 Positive (TP=4, FN=0)
  • 정상(6) → 전부 Positive (FP=6, TN=0)

• TPR = 4 / (4+0) = 1.0

• FPR = 6 / (6+0) = 1.0

→ ROC 상에서 점: (FPR=1.0, TPR=1.0)

---

3. ROC 곡선 그리기

위와 같은 식으로 여러 Threshold에 대해 (FPR, TPR) 쌍을 구하고, 이를 x축=FPR, y축=TPR 좌표평면에 찍은 다음, 연결하면 ROC 곡선이 됩니다.

예시의 (FPR, TPR) 좌표들을 순서대로 나열해보면:

1. Threshold = 1.00 → (0.0, 0.0)
2. Threshold = 0.80 → (0.0, 0.5)
3. Threshold = 0.55 → (0.0, 1.0)
4. Threshold = 0.30 → (0.33, 1.0)
5. Threshold = 0.00 → (1.0, 1.0)

이 점들을 이어서 그리면 아래와 같은 형태가 됩니다(대략적인 스케치):

TPR
1.0 |         •----•----• (threshold 0.30 → 0.00)
    |         |          \
0.5 |         • (threshold 0.80)
    |         
0.0 |  • (threshold 1.00)
    |_______________________________________ FPR
       0.0              0.33           1.0

• FPR=0~1, TPR=0~1 범위 내에서 곡선(혹은 꺾은선)이 그려진다고 보면 됩니다.
• 일반적으로는 Threshold가 높을수록 FPR과 TPR 모두 낮아지고, Threshold를 낮출수록 FPR과 TPR 모두 올라갑니다.

4. 해석

1. ROC 곡선은 모델이 Threshold를 변화시켰을 때, 위양성(FP)을 얼마나 감수하고서 얼마나 많은 Positive(스팸)를 잡아낼 수 있는지(TP)를 시각화합니다.
2. 왼쪽 위 모서리(0,1)에 가까울수록 “FPR은 거의 없고, TPR은 높은” 이상적인 모델에 가깝습니다.
3. (0,0) → (1,1) 대각선을 기준으로, ROC 곡선이 이 대각선보다 위쪽에 많이 위치할수록 모델 성능이 좋다고 말합니다.
4. ROC 곡선 아래 면적을 AUC(Area Under the ROC Curve)라고 부르며, 1에 가까울수록 (즉 곡선이 왼쪽 위 모서리로 치우칠수록) 더 좋은 분류기를 의미합니다.

결론적으로

• ROC 곡선은 “TPR vs FPR”를 다양한 임계값에서 변화시키며 관찰한 결과를 시각화한 그래프입니다.
• 예시처럼 각 Threshold마다 “어떻게 (TP, FP, TN, FN)이 변하는지”를 계산하고, TPR과 FPR을 구해서 x-y 평면 위에 점을 찍고 이어주면 됩니다.
• ROC 곡선을 보면, 모델이 긍정(스팸) 클래스를 얼마나 잘 잡아내는지(TPR)와 부정(정상) 클래스를 얼마나 잘 구분하지 못했는지(FPR) 사이의 트레이드오프를 한눈에 파악할 수 있습니다.

---

4. The Area Under ROC Curve

AUC(Area Under the ROC Curve)는 ROC 곡선 아래 면적을 0~1 사이 값으로 표현한 단일 수치 지표입니다. (AUC: Area Under ROC Curve)

• AUC = 0.5이면 무작위 분류 수준,
• AUC = 1.0이면 완벽한 분류를 의미합니다.
• AUC는 특정 임계치나 클래스 비율, 비용/이익 구조를 몰라도 모델의 전반적인 판별 능력을 하나의 수치로 쉽게 비교할 수 있어 유용합니다.(AUC is a good general summary statistics of the predictiveness of a classifier)

---

5. Cumulative Response and Lift Curves(누적응답곡선, 향상도)

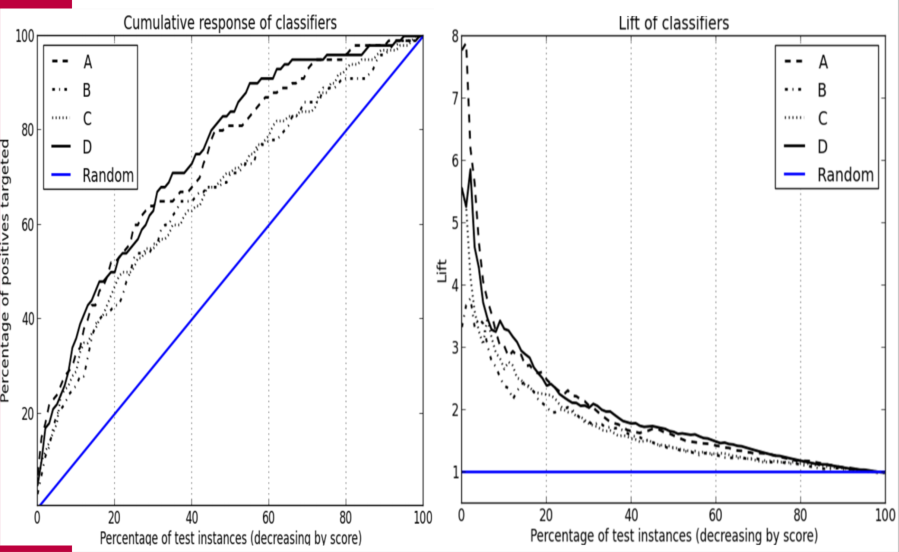
누적 응답 곡선(Cumulative Response Curve)은 모델이 상위 X%의 사례를 긍정으로 분류했을 때, 실제 긍정 사례를 얼마나 포함하는지를 Y축에 나타낸 그래프입니다.

• 대각선(랜덤선)보다 위에 위치할수록 모델이 무작위보다 더 많은 긍정 사례를 상위권에 배치한다는 의미입니다.

• 향상도(Lift)는 무작위 분류 대비 모델이 얼마나 더 효율적으로 긍정 사례를 상위로 끌어올렸는지 보여주는 지표입니다.(The lift curve is essentially the value of the cumulative response curve at a given x point divided by the diagonal line (y=x) at that point)

• 이러한 곡선을 통해 비용/이익을 명확히 산정하기 어렵더라도, 어떤 모델이 상대적으로 더 우수한 순위화 성능을 가지는지 비교할 수 있습니다.

Cumulative response curves plot the hit rate (tp rate; y axis), i.e., the percentage of positive correctly classified, as a function of the percentage of the population that is targeted (x axis). (X모집단에서 타겟팅한 비율, y는 올바로 분류한 진양성율 )

The lift is the degree to which it “pushes up” the positive instances in a list above the negative instances.

---

6. Summary

• 모델 평가 시 단순 정확도 뿐 아니라, 클래스 비율(사전확률), 비용/이익을 종합적으로 고려하는 기대 가치(Expected Value) 기반 평가가 중요합니다.

• Profit graph can be useful to compare models of interest under a range of conditions.(모델 운용 조건 명시 필요 )

• 정확한 확률을 모르더라도 순위 정보만으로 효율적인 의사결정을 내릴 수 있습니다.

• 비용/이익 구조와 사전확률이 명확할 때는 수익곡선(Profit Curves)을, 불확실할 때는 ROC 커브나 누적 응답/향상도 곡선을 활용할 수 있습니다.

• AUC, 누적응답곡선, Lift 그래프 등은 다양한 상황에서 모델 성능을 비교하고 해석하는 유용한 도구를 제공합니다.

• ROC 그래프는 모델이 얼마나 잘 긍정 클래스를 잡아내는지(참양성비율)와 그 과정에서 음성 클래스를 얼마만큼 잘못 긍정으로 오분류하는지(거짓양성비율)를 “순수하게” 보여주며, 이 두 값 사이의 근본적인 상호관계(트레이드오프)를 객관적으로 파악할 수 있도록 해주는 도구(ROC graphs are independent of the class proportions as well as the costs and benefits. (중요 !!))