SDEdit : https://arxiv.org/pdf/2108.01073
(AI_tech에서 멤버가 해서 그냥 나도 읽어본다ㅋㅋ)

0. Abstract

Guided image synthesis enables everyday users to create and edit photo-realistic images with minimum effort. The key challenge is balancing faithfulness to the user inputs (e.g., hand-drawn colored strokes) and realism of the synthesized images.

📖 Guided Image Synthesis는 최소한의 노력으로 realistic 한 포토이미지들을 수정(edit)하게 해주는 것. 중요한 점은 faithfullness와 realism의 균형 이다!!

🤔 faithfullness와 realism 이 무슨 말이야?

✍️ 충실성(faithfullness) : 생성된 이미지가 사용자의 입력이나 가이드에 얼마나 잘 맞추어 졌는지 말함.
사실성(realism) : 생성된 이미지가 얼마나 현실적으로 보이는지 말함

즉, 생성된 이미지가 사용자가 원하는 가이드에 맞추면서 동시에 사실적으로 보여줘야함. 한쪽으로만 치우친다면 원하는 이미지가 이루어지지 않는다는 말임.

Existing GAN-based methods attempt to achieve such balance using either conditional GANs or GAN inversions, which are challenging and often require additional training data or loss functions for individual applications. To address these issues, we introduce a new image synthesis and editing method, Stochastic Differential Editing (SDEdit), based on a diffusion model generative prior, which synthesizes realistic images by iteratively denoising through a stochastic differential equation (SDE).

Given an input image with user guide in a form of manipulating RGB pixels, SDEdit first adds noise to the input, then subsequently denoises the resulting image through the SDE prior to increase its realism. SDEdit does not require task-specific training or inversions and can naturally achieve the balance between realism and faithfulness.

📖(1) 기존 문제점:
기존의 GAN방법들은 조건부GAN 또는 GAN inversion을 사용하여 균형을 이루려고 하지만 이는 추가적인 학습데이터나 loss function이 필요

(2) 해결방법:
SDEdit(디퓨전 모델 생성 사전을 기반으로 하는) 모델을 제안하고 이는 확률적 미분 방정식(SDE)을 통해 반복적으로 노이즈를 제거하여 현실감 있는 이미지 생성

(3) 방법론:
먼저 입력이미지에 노이즈를 더하고 그 후에 현실감을 높이기 위해 SDE prior를 통해 디노이징 시킨다. -> 이는 특별한 task-spcific training 이 필요하지 않다..!

1. Introduction

(...)
To balance realism and faithfulness while avoiding the previously mentioned challenges, we introduce SDEdit, a guided image synthesis and editing framework leveraging generative stochastic differential equations (SDEs; Song et al., 2021). Similar to the closely related diffusion models (SohlDickstein et al., 2015; Ho et al., 2020), SDE-based generative models smoothly convert an initial Gaussian noise vector to a realistic image sample through iterative denoising, and have achieved unconditional image synthesis performance comparable to or better than that of GANs (Dhariwal & Nichol, 2021)

📖 SDE-Based생성모델은 초기의 가우시안 노이즈벡터를 반복적인 노이즈 제거를 통해 현실적인 이미지샘플로 부드럽게 변환한다.

뭐야 디퓨전이잖아

The key intuition of SDEdit is to “hijack” the generative process of SDE-based generative models, as illustrated in Fig. 2. Given an input image with user guidance input, such as a stroke painting or an image with stroke edits, we can add a suitable amount of noise to smooth out undesirable artifacts and distortions (e.g., unnatural details at stroke pixels), while still preserving the overall structure of the input user guide. We then initialize the SDE with this noisy input, and progressively remove the noise to obtain a denoised result that is both realistic and faithful to the user guidance input (see Fig. 2).

📖 SDEdit의 가장 직관적인 핵심은 가로채는(hijack) 것입니다..! 유저가 입력을 넣으면(guidance input) 적절한 노이즈를 추가하여 바람직하지 않은 인공물이나 왜곡을 부드럽게(smooth)하는것.

Unlike conditional GANs, SDEdit does not require collecting training images or user annotations for each new task; unlike GAN inversions, SDEdit does not require the design of additional training or task-specific loss functions. SDEdit only uses a single pretrained SDE-based generative model trained on unlabeled data: given a user guide in a form of manipulating RGB pixels, SDEdit adds Gaussian noise to the guide and then run the reverse SDE to synthesize images. SDEdit naturally finds a trade-off between realism and faithfulness: when we add more Gaussian noise and run the SDE for longer, the synthesized images are more realistic but less faithful. We can use this observation to find the right balance between realism and faithfulness

📖 SDEdit 가 좋은점
① training image 와 유저 annotations가 필요하지 않음
② task- loss function 이 필요하지 않음
③ 사전학습된(pre-trained) SDE기반 생성 모델만을 사용함.

---

[Fig2](전반적인 SDEdit 의 설명이 나와있다.)

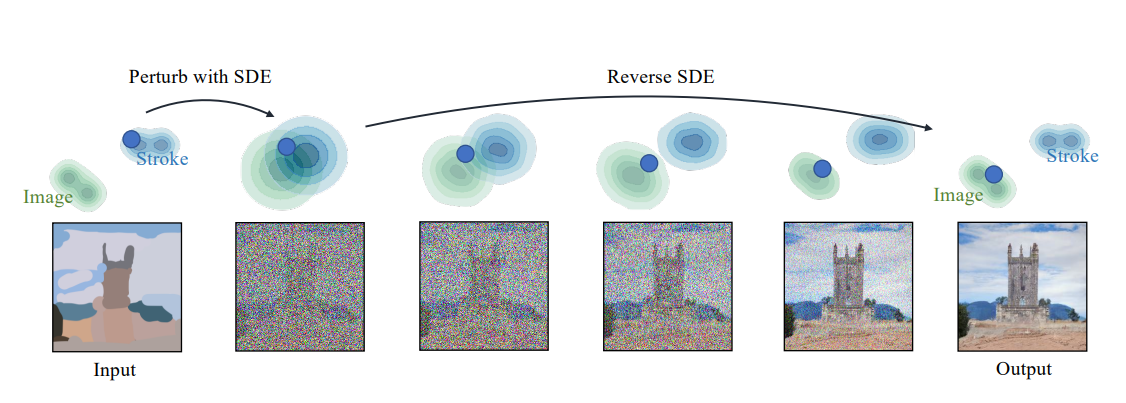
Figure 2: Synthesizing images from strokes with SDEdit. The blue dots illustrate the editing process of our method. The green and blue contour plots represent the distributions of images and stroke paintings, respectively. Given a stroke painting, we first perturb it with Gaussian noise and progressively remove the noise by simulating the reverse SDE. This process gradually projects an unrealistic stroke painting to the manifold of natural images

✍️ stroke painting 을 주고 첫번째로 ① perturb it with gaussian noise -> 가우시안 노이즈를 주고!
② 그 후에 점진적으로 reveser SDE를 통해서 노이즈를 제거함
--> 이렇게 하면 부현실적인 stroke painting이ㅣ 자연스러운 natural images로 변환한다고함!

---

2. BackGround: Image Synthesis With Stochastic Diffential Equations(SDEs)

Stochastic differential equations (SDEs) generalize ordinary differential equations (ODEs) by injecting random noise into the dynamics. The solution of an SDE is a time-varying random variable(i.e., stochastic process), which we denote as $x(t) \in \mathbb{R^d}$, where $t \in [0, 1]$ indexes time.
In image synthesis (Song et al., 2021), we suppose that $x(0) ∼ p_0 = p_{data}$ represents a sample from the data distribution and that a forward SDE produces $x(t) \text{ for } t \in (0,1]$via a Gaussian diffusion. Given $x(0)$, $x(t)$ is distributed as a Gaussian distribution:

$x(t) = α(t)x(0) + σ(t)z, z ∼ N (0, I)$

where $σ(t)$ : $[0, 1] → [0, ∞)$ is a scalar function that describes the magnitude of the noise $z$, and $α(t) : [0, 1] → [0, 1]$ is a scalar function that denotes the magnitude of the data $x(0)$. The probability density function of $x(t)$ is denoted as $p_t$.

📖 SDEs(확률적 미분방정식)은 보통의 미분방정식(ODEs)를 확장한 것으로 시스템 동역학에 무작위 노이즈를 주입하여(injecting) 하여 확률적 요소를 포함하는 것. SDEs의 해는 시간에 따라 변화하는 확률변수이다.
$x(0) ∼ p_0 =p_{data}$은 데이터 분포로부터 의 샘플
$x(t)$는 가우시안 노이즈가 추가된 시간$t$에 따른 샘플
$\alpha(t) , \sigma(t)$ : 시간에 따라 변화하는 계수들로 데이터의 스케일과 노이즈의 세기 조절.
$z \sim N(0,I)$ : 평균이 0 , 공분산이 단위행렬인 가우시안 노이즈

Two types of SDE are usually considered: ①the Variance Exploding SDE (VE-SDE) has $α(t) = 1$ for all $t$ and $σ(1)$ being a large constant so that $p_1$ is close to $N (0, σ^2(1)I)$; whereas
②the Variance Preserving (VP) SDE satisfies $α^2(t) + σ^2(t) = 1$ for all $t$ with $α(t) → 0$ as $t → 1$ so that $p_1$ equals to $N (0, I)$. Both VE and VP SDE transform the data distribution to random Gaussian noise as $t$ goes from 0 to 1. For brevity, we discuss the details based on VE-SDE for the remainder of the main text,and discuss the VP-SDE procedure in Appendix C. Though possessing slightly different forms and performing differently depending on the image domain, they share the same mathematical intuition.

📖 SDE 는 2가지 유형이 있다
① 첫번째는, 분산 폭발(VE_Variance Exploding)로 $\alpha(t) = 1$ 로 고정되고 $\sigma(1)$ 은 매우 큰 값

② 두번째는, 분산 유지(VP_Variance Preserving)로 $\alpha(t)^2 + \sigma(t)^2 =1$이며 이는 시간이 지나면서 $\alpha(t)$ 는 0에 가까워진다. 결국 $p_1$은 평균0 분산1인 $N(0,I)$로 가까워진다.(표준정규분포화 됨)

🤔 의문점이 생긴다. 왜 $\sigma(1)$은 매우 큰 값이고 $p_1$은 뭔가?

✍️ ① $\sigma(1)$은 매우 큰 값인 이유
-> 데이터의 노이즈가 시간에 따라 점점 더 커지면서 최종적으로는 매우 큰 분산을 갖는 가우시간 분포로 확대된다는 것인다 $\sigma(1)$ 이 크다는 것은 이 과정에서 분산이 매우 크게 확대됨을 의미하므로!
② $p_1$ 의 의미?
-> 우리 그전에 $t$는 시간을 가리킨다고 했고 범위는 $(0,1]$ 이었다.
따라서 $p_1$은 시간 $t =1$에서의 데이터 분포를 나타내며 최종적인 결과물이라고 할 수 있다.
-> 우리 SDE의 목표는 초기 데이터분포 $p_0$을 점진적으로 변형하여 최종적으로 원하는 분포 $p_1$을 만드는 것이라고 볼 수 있다.

• 추가로 위 논문에서는 VE-SDE를 쓴다고 하였다.

Image synthesis with VE-SDE. Under these definitions, we can pose the image synthesis problem as gradually removing noise from a noisy observation $x(t)$ to recover $x(0)$. This can be performed via a reverse SDE (Anderson, 1982; Song et al., 2021) that travels from $t = 1$ to $t = 0$, based on the knowledge about the noise-perturbed score function $\nabla_x \log p_t(x)$. For example, *the sampling procedure for VE-SDE is defined by the following (reverse) SDE:

$dx(t) =[\frac{d[\sigma^2(t)]}{dt} \nabla_x \log p_t(x)]dt +\sqrt{\frac{d[\sigma^2(t)]}{dt}}$

where $\tilde w$ is a Wiener process when time flows backwards from $t = 1$ to $t = 0$. If we set the initial conditions $x(1) \sim p_1 = N (0, σ^2(1)I)$, then the solution to $x(0)$ will be distributed as $p_{data}$. In practice, the noise-perturbed score function can be learned through denoising score matching

📖 ①Score function 은 $\nabla_x \log p_t(x)$ 이고
②역방향 SDE(reverse SDE)는 $dx(t) =[\frac{d[\sigma^2(t)]}{dt} \nabla_x \log p_t(x)]dt +\sqrt{\frac{d[\sigma^2(t)]}{dt}}$ 이다.
③ $\tilde w$ 는 Wiener process 이며 사건아 $t =1$ 에서 $t =0$으로 역방향(bakward)흐를 때의 Wiener 과정이다. <- 실전에서 denoising score matching 을 통해서 noise-perturbed score function 을 배울 수 있다.

🤔 이제 조금만 더 산을 넘으면 된다.. 📖에 있는 1,2,3 모두 무슨 말인지 모르겠다. 하지만 천천히 조금씩 해부하다 보면은 알 수 있다..!

✍️ 해부시작.
① Score function $\nabla_x \log p_t(x)$ 의 의미:

• $p_t(x)$ : 시간 $t$에 따른 이미지 $x$의 확률 밀도 함수 -> 노이즈가 추가된 이미지 $x$ 가 시간 $t$에서 얼마나 가능한지 나타냄

• $log \ p_t(x)$ : 확률밀도함수이고 간단하고 계산을 용이하게 함.

• $\nabla_x \log p_t(x)$ : 이미지 $x$에 대한 그레디언드(기울기) -> 이는 이미지 $x$의 각 픽셀에 대해서 $log \ p_t(x)$ 가 얼마나 빠르게 변화하는지를 나타냄. ->즉 $x$의 값이 바뀔 때, $log \ p_t(x)$ 의 변화율!

3. Guided Image Synthesis and Edititing With SDEdit

4. Related Work

5. Experiments

5.1) Stroke-Based Image Synthesis

5.2) Flexible Image Editing

6. Conclusion