Tree

jung_ho9 개발일지·2023년 1월 13일

자료구조/알고리즘

목록 보기

5/13

Tree 란

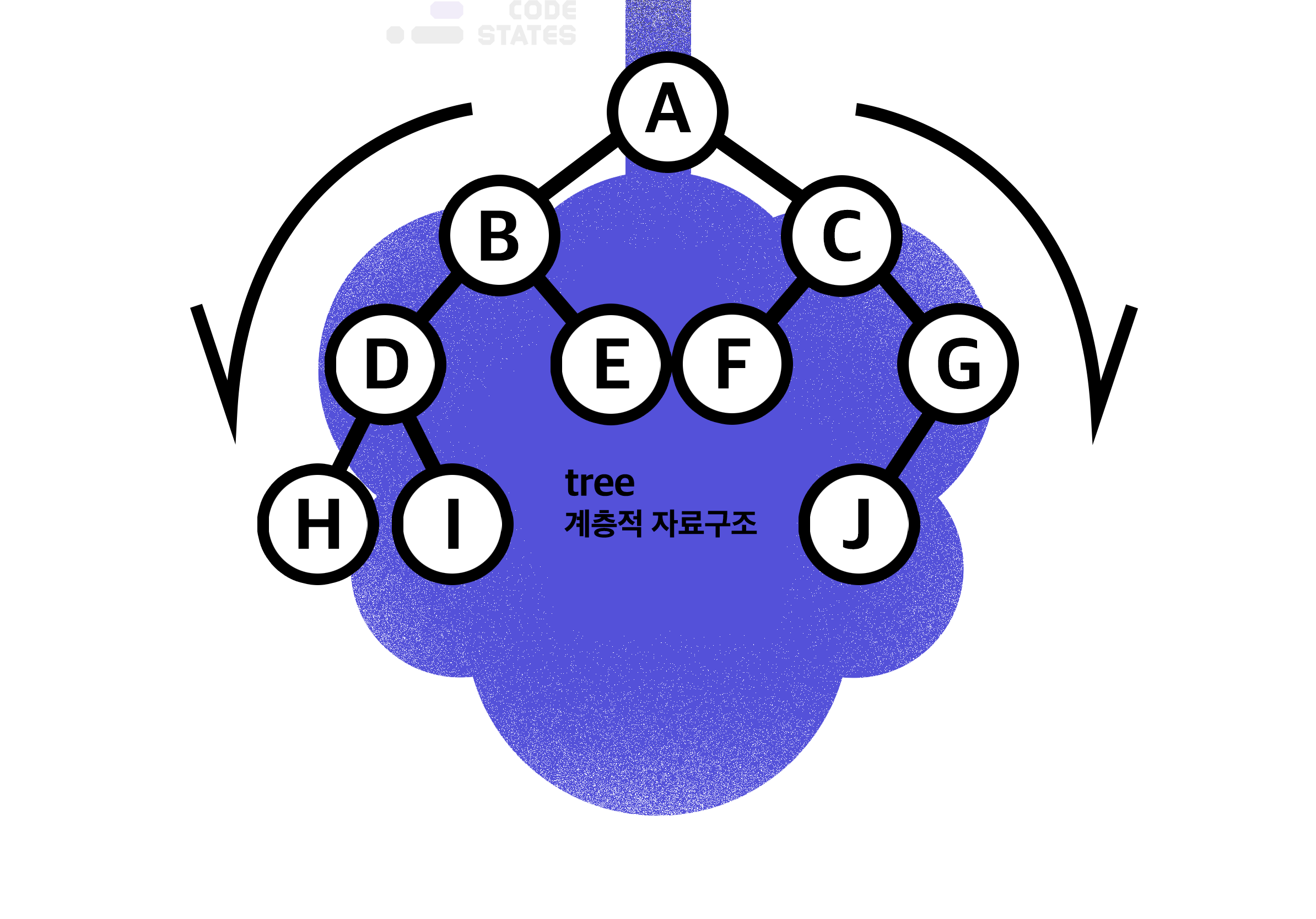
자료구조 Tree는 그래프의 여러 구조 중 단방향 그래프의 한 구조로, 하나의 뿌리로부터 가지가 사방으로 뻗은 형태가 나무와 닮아 있다고 해서 트리 구조라고 부른다.

마치 가계도와 흡사해 보이는 이 트리 구조는 데이터가 바로 아래에 있는 하나 이상의 데이터에 한 개의 경로와 하나의 방향으로만 연결된 계층적 자료구조다.
데이터를 순차적으로 나열시킨 선형 구조가 아니라, 하나의 데이터 아래에 여러 개의 데이터가 존재할 수 있는 비선형 구조다.
트리 구조는 계층적으로 표현이 되고, 아래로만 뻗어나가기 때문에 사이클(cycle)이 없다. 여기서 사이클이란 시작 노드에서 출발해 다른 노드를 거쳐 시작 노드로 돌아올 수 있다면 사이클이 존재한다고 표현한다.
따라서 트리는 사이클(cycle)이 없는 하나의 연결 그래프 (Connected Graph)라고 할 수 있다.

Tree 구조와 특징

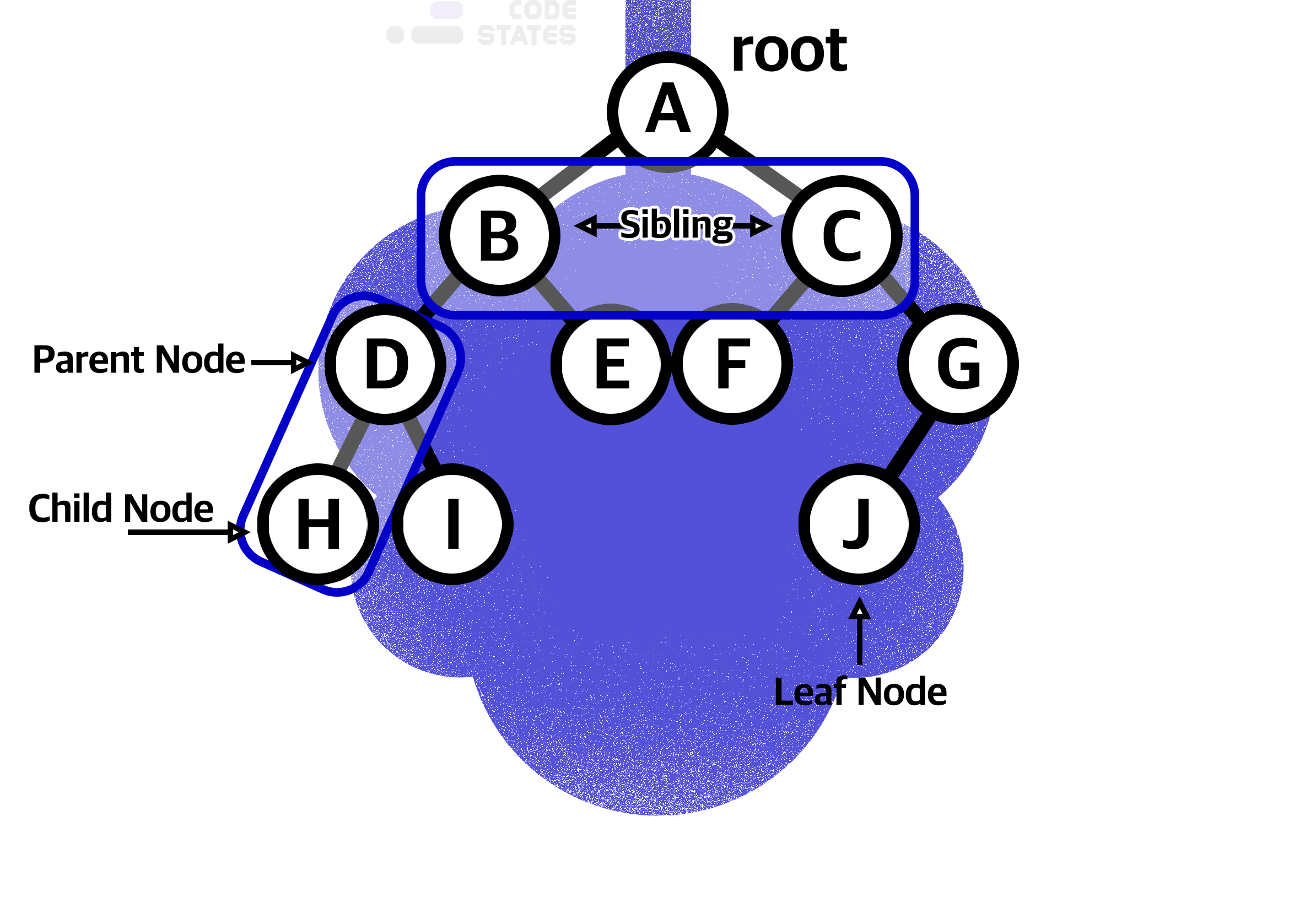
트리 구조는 루트(Root) 라는 하나의 꼭짓점 데이터를 시작으로 여러 개의 데이터를 간선(edge)으로 연결한다. 각 데이터를 노드(Node)라고 하며, 두 개의 노드가 상하 계층으로 연결되면 부모/자식 관계를 가진다.
위 그림에서 A는 B와 C의 부모 노드(Parent Node)이고, B와 C는 A의 자식 노드(Child Node)다.
자식이 없는 노드는 나무의 잎과 같다고 하여 리프 노드(Leaf Node)라고 부른다.

깊이 (depth)

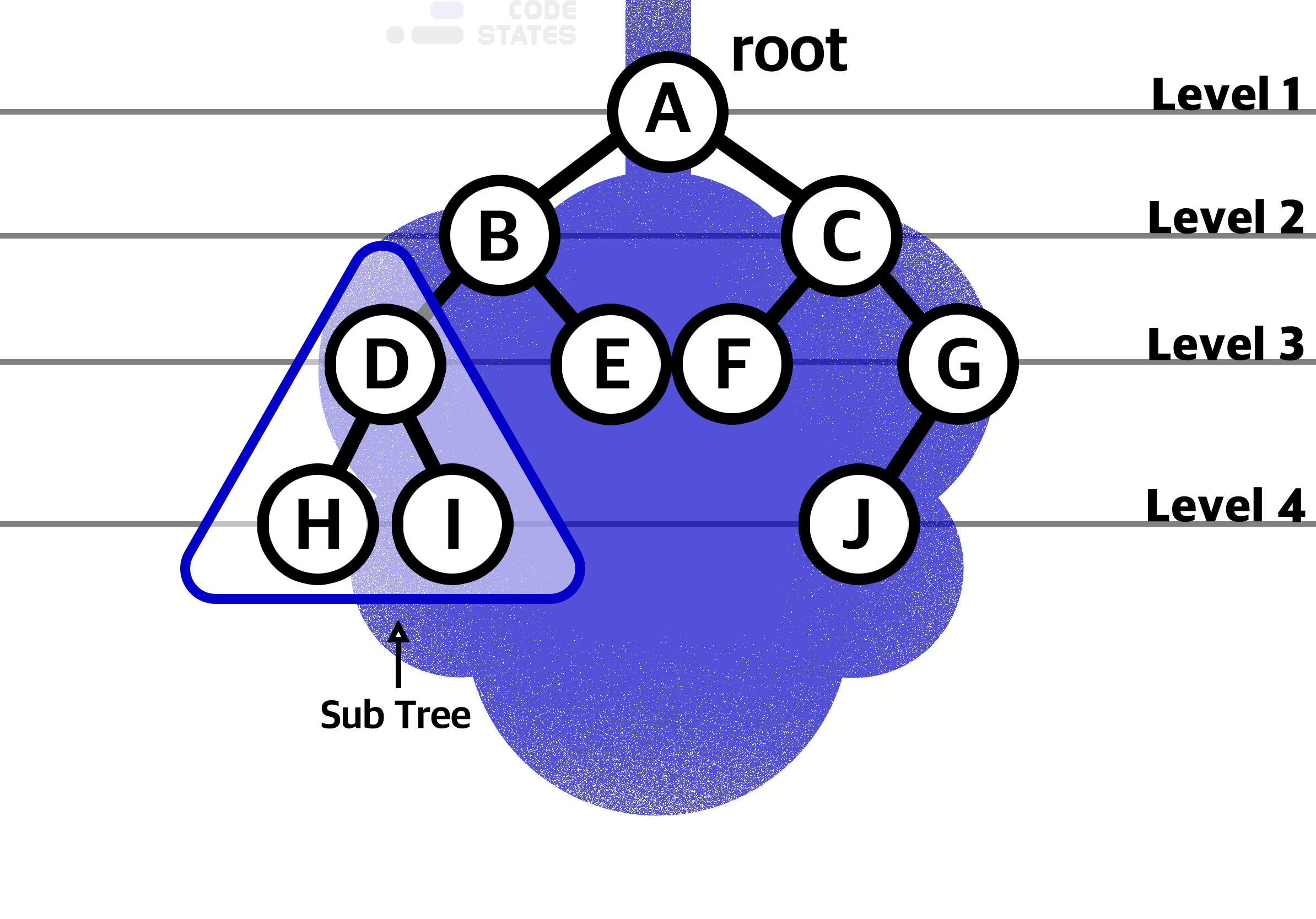
트리 구조에서는 루트로부터 하위 계층의 특정 노드까지의 깊이(depth)를 표현할 수 있다. 위 그림에서 루트노트인 A의 depth는 0, B와 C의 깊이는 1, D, E, F, G의 깊이는 2가 된다.

레벨 (Level)

트리 구조에서 같은 깊이를 가지고 있는 노드를 묶어서 레벨(level)로 표현할 수 있다. depth가 0인 루트 A의 level은 1, depth가 1인 B와 C의 level은 2, D, E, F, G의 레벨은 3이 되며 같은 레벨에 나란히 있는 노드를 형제 노드(Sibling Node) 라고 한다.

서브 트리(sub tree)

트리 구조의 root에서 뻗어 나오는 큰 트리의 내부에, 트리 구조를 갖춘 작은 트리를 서브 트리라고 부른다. (D, H, I)로 이루어진 작은 트리도 서브 트리이고, (B, D, E)나 (C, F, G, J)도 서브 트리입니다

용어정리

노드(Node) : 트리 구조를 이루는 모든 개별 데이터
루트(Root) : 트리 구조의 시작점이 되는 노드
부모 노드(Parent node) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 가까운 노드
자식 노드(Child node) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 먼 노드
리프(Leaf) : 트리 구조의 끝 지점이고, 자식 노드가 없는 노드

Tree의 실사용 예제

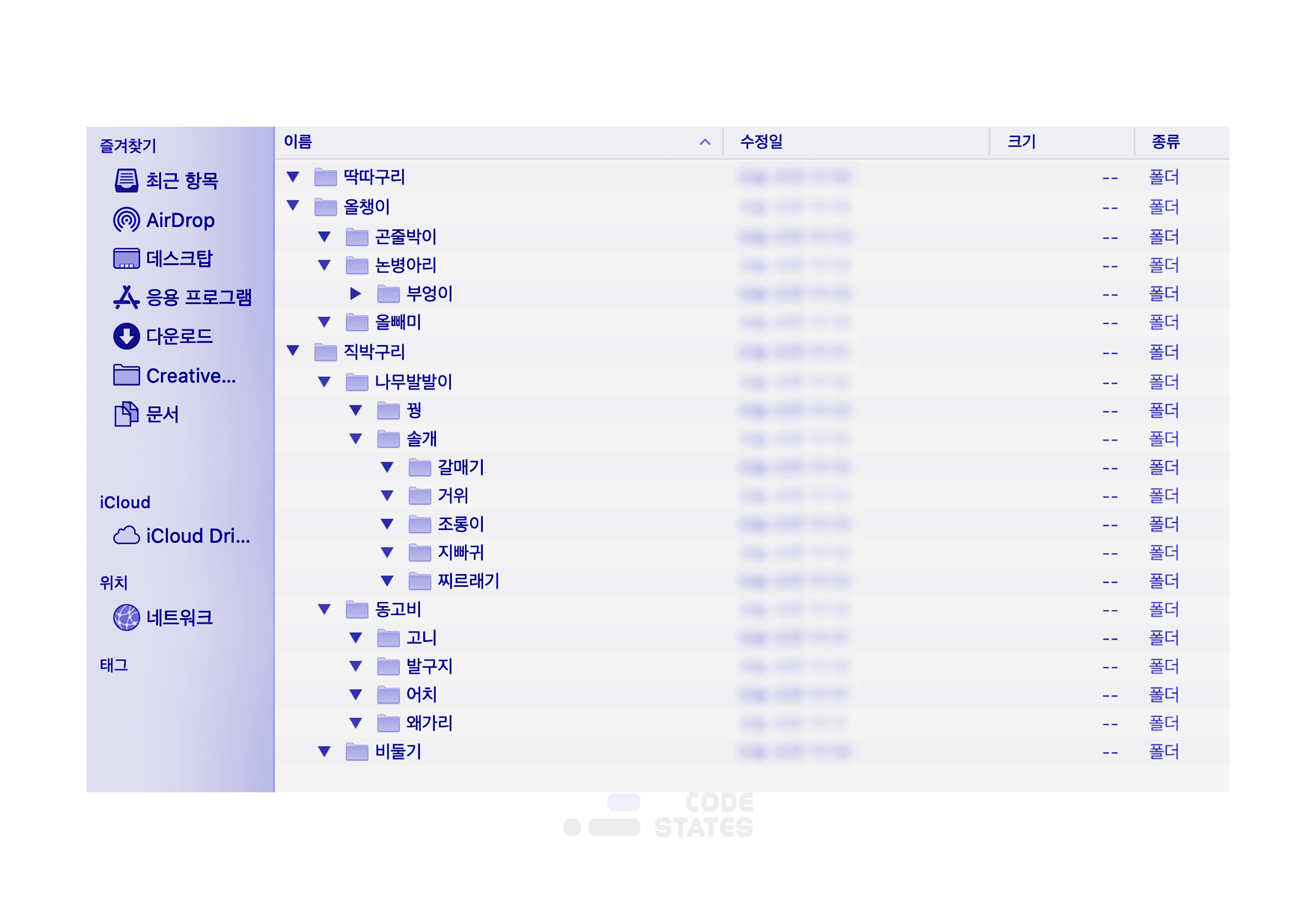
가장 대표적인 Tree의 예제는 컴퓨터의 디렉토리 구조다. 어떤 프로그램이나 파일을 찾을 때, 바탕화면 폴더나 다운로드 폴더 등에서 다른 폴에 진입하고, 또 그 안에서 다른 폴더에 진입하면서 원하는 프로그램이나 파일을 찾는다. 모든 폴더는 하나의 폴더(루트 폴더,/)에서 시작되어 가지를 뻗어나가는 모양새를 띄고있다.