
최소 신장 트리(MST)
최소 신장 트리(MST)는 여러 개의 점(정점)과 선(간선)으로 이루어진 그림(그래프)에서 모든 점들을 최소한의 비용으로 연결하는 방법이에요. 예를 들어, 여러 도시를 가장 짧은 길로 연결하는 것을 생각해보세요! 모든 점들이 서로 연결되면서 최소한의 비용(가중치)으로 연결되는 것이 가장 중요해요.
신장 트리란?
- 신장 트리는 모든 점들이 연결된 트리로, 사이클(빙글빙글 도는 길)이 없고 점들이 모두 연결된 구조예요.
- 최소 신장 트리(MST)는 이 트리에서 가장 비용이 적게 드는 방식으로 점들을 연결한 거예요.
MST를 구하는 이유
최소 비용이나 최적의 경로를 찾는 문제를 해결할 때 많이 사용돼요. 예를 들어, 도시들 간의 도로를 최소한의 길이로 연결하거나, 전선으로 모든 집을 연결할 때 쓸 수 있어요.
MST를 구하는 방법으로는 크루스칼 알고리즘과 프림 알고리즘이 있어요.
1. 크루스칼 알고리즘(Kruskal)
크루스칼 알고리즘은 선(길)을 중심으로 점들을 연결하는 방법이에요. 아래는 코드와 함께 설명해볼게요.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Kruskal {
static int V, E;
static int[] parent;
static class Edge implements Comparable<Edge> {
int start;
int end;
int weight;
public Edge(int start, int end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
@Override
public int compareTo(Edge o) {
return this.weight - o.weight;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
V = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
PriorityQueue<Edge> pq = new PriorityQueue<>();
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
pq.add(new Edge(start, end, weight));
}
makeSet();
int cnt = 0;
int totalWeight = 0;
while (!pq.isEmpty()) {
Edge edge = pq.poll();
if (union(edge.start, edge.end)) {
totalWeight += edge.weight;
System.out.println(edge.start + "-" + edge.end + " 연결, 누적 weight: " + totalWeight);
if (++cnt == V - 1)
break;
}
}
}
public static void makeSet() {
parent = new int[V + 1];
for (int i = 1; i <= V; i++) {
parent[i] = i;
}
}
public static int find(int x) {
if (x == parent[x])
return x;
return parent[x] = find(parent[x]);
}
public static boolean union(int x, int y) {
x = find(x);
y = find(y);
if (x == y)
return false;
if (x <= y)
parent[y] = x;
else
parent[x] = y;
return true;
}
}입력 예시
5 10 1 2 5 1 3 10 1 4 8 1 5 7 2 3 5 2 4 3 2 5 6 3 4 1 3 5 3 4 5 1
출력 예시
3-4 연결, 누적 weight: 1 4-5 연결, 누적 weight: 2 2-4 연결, 누적 weight: 5 1-2 연결, 누적 weight: 10
크루스칼 알고리즘은 간선의 가중치(비용)를 기준으로 정렬해서 가장 작은 가중치부터 차례대로 연결해요. 이때 사이클(순환)이 생기지 않도록 조심해야 해요. 그래서 Union-Find 알고리즘을 이용해서 두 점이 같은 그룹인지 확인해요.
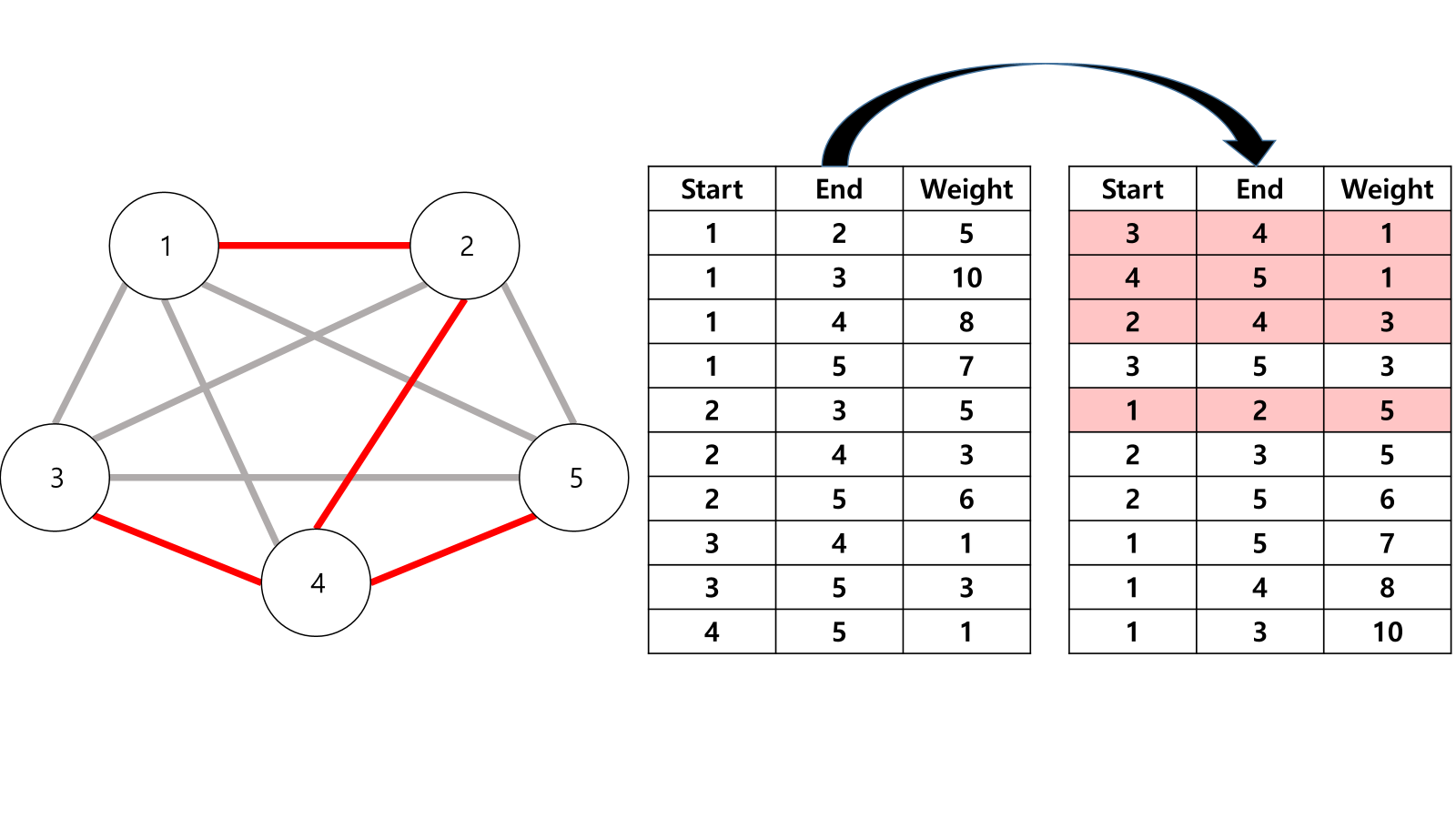
코드와 그림에서 볼 수 있듯이, 크루스칼 알고리즘은 간선(길)을 중심으로 동작해요. 크루스칼은 간선의 비용(가중치)을 기준으로 가장 작은 것부터 차례대로 선택해요. 여기서 우선순위 큐라는 도구를 사용해서 비용이 가장 낮은 간선을 빠르게 뽑을 수 있어요.
2. 프림 알고리즘(Prim)
프림 알고리즘은 정점(점)을 중심으로 점들을 연결하는 방법이에요. 임의의 점에서 시작해서 최소 비용으로 연결할 수 있는 다음 점을 선택해요.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Prim {
static int V, E;
static boolean[] visited;
static int[] minEdge;
static ArrayList<Vertex>[] nodeList;
static class Vertex implements Comparable<Vertex> {
int no;
int weight;
public Vertex(int no, int weight) {
this.no = no;
this.weight = weight;
}
@Override
public int compareTo(Vertex o) {
return this.weight - o.weight;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
V = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
nodeList = new ArrayList[V + 1];
visited = new boolean[V + 1];
minEdge = new int[V + 1];
for (int i = 1; i <= V; i++) {
nodeList[i] = new ArrayList<>();
minEdge[i] = Integer.MAX_VALUE;
}
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
nodeList[start].add(new Vertex(end, weight));
nodeList[end].add(new Vertex(start, weight));
}
PriorityQueue<Vertex> pq = new PriorityQueue<>();
minEdge[1] = 0;
pq.offer(new Vertex(1, minEdge[1]));
int cnt = 0;
int totalWeight = 0;
while (!pq.isEmpty()) {
Vertex vertex = pq.poll();
if (!visited[vertex.no]) {
totalWeight += vertex.weight;
visited[vertex.no] = true;
System.out.println(vertex.no + ", 누적 weight: " + totalWeight);
for (Vertex next : nodeList[vertex.no]) {
if (!visited[next.no] && minEdge[next.no] > next.weight) {
minEdge[next.no] = next.weight;
pq.offer(new Vertex(next.no, minEdge[next.no]));
}
}
if (++cnt == V)
break;
}
}
}
}입력 예시
5 10 1 2 5 1 3 10 1 4 8 1 5 7 2 3 5 2 4 3 2 5 6 3 4 1 3 5 3 4 5 1
출력 예시
1, 누적 weight: 0 2, 누적 weight: 5 4, 누적 weight: 8 3, 누적 weight: 9 5, 누적 weight: 10
프림 알고리즘은 시작점에서 연결된 점 중에서 가장 비용이 적은 점을 선택해요. 점을 하나씩 연결하면서 그 점과 연결된 길들을 큐에 넣고, 그중에서 가장 작은 비용의 길을 뽑아내는 방식이에요.
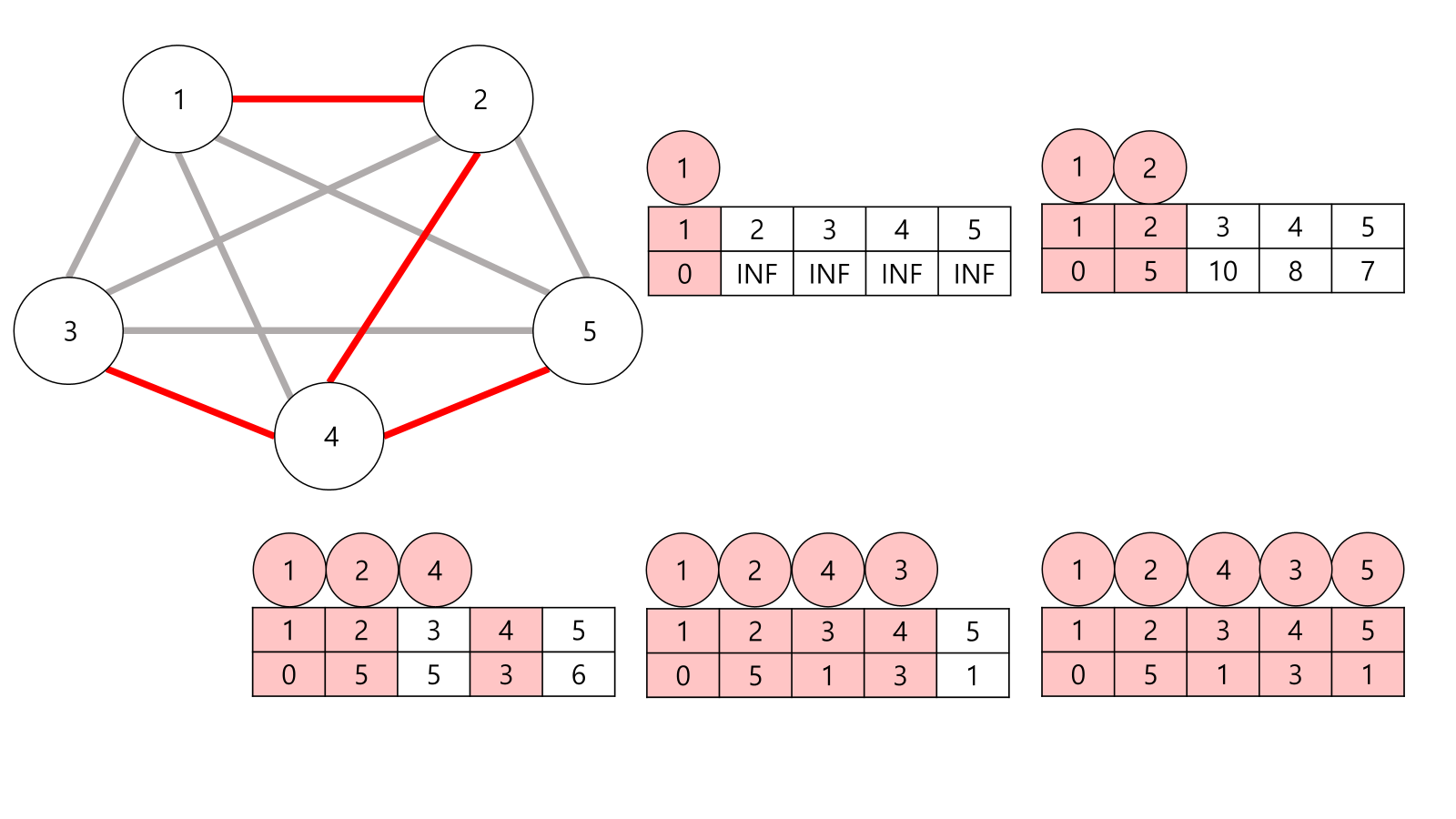
정리
- 최소 신장 트리(MST)는 그래프에서 모든 점을 최소한의 비용으로 연결하는 방법이에요. 크루스칼과 프림 알고리즘은 각각 선과 점을 중심으로 MST를 찾아요.
- 크루스칼 알고리즘은 정점이 많을 때 적합해요.
- 프림 알고리즘은 간선이 많을 때 유리해요.
둘 다 중요한 알고리즘이니 기억해두고, 문제를 풀 때 어떤 방법이 더 적합할지 생각해보면 좋아요!

LGTM