
서로소 집합(Disjoint Set)과 Union-Find 알고리즘
- 서로소 집합(Disjoint Set)은 여러 개의 물건이나 요소가 서로 연결되어 있는지 또는 서로 다른 그룹에 속해 있는지를 판단하는 자료구조예요. 예를 들어, 친구 관계를 생각해보세요. 친구의 친구는 나와 같은 그룹에 속할 수 있겠죠? 이런 식으로 서로 연결된 그룹을 찾는 데 사용되는 방법이에요.
Union-Find 알고리즘은 크게 세 가지 단계로 나눠 볼 수 있어요:
- makeSet: 모든 요소가 자기 자신을 그룹의 대표(루트)로 가지게 초기화해요.
- find: 어떤 요소가 속한 그룹의 대표를 찾는 함수예요.
- union: 두 요소가 속한 그룹을 하나로 합치는 함수예요.
Union-Find 알고리즘
- 모든 요소를 자기 자신을 대표로 초기화해요. (예: 각 학생이 자기를 대표라고 생각해요)
- find 함수는 어떤 요소가 속한 그룹의 대표(루트)를 찾는 함수예요.
- union 함수는 두 요소의 루트를 찾아 같은 그룹으로 만드는 거예요.
아래 코드는 기본적인 Union-Find 알고리즘을 보여줘요.
import java.util.Arrays;
public class DisjointSet {
static int N;
static int[] parent;
public static void makeSet() {
parent = new int[N + 1];
for (int i = 1; i <= N; i++) {
parent[i] = i;
}
}
public static int find(int x) {
if (x == parent[x])
return x;
return find(parent[x]);
}
public static void union(int x, int y) {
x = find(x);
y = find(y);
if (x <= y)
parent[y] = x;
else
parent[x] = y;
}
public static void main(String[] args) {
N = 6;
makeSet();
System.out.println(Arrays.toString(parent));
union(1, 2);
System.out.println(Arrays.toString(parent));
union(3, 4);
System.out.println(Arrays.toString(parent));
union(1, 5);
System.out.println(Arrays.toString(parent));
union(3, 5);
System.out.println(Arrays.toString(parent));
}
}
출력 예시
[0, 1, 2, 3, 4, 5, 6] // 초기 상태
[0, 1, 1, 3, 4, 5, 6] // union(1, 2) 이후
[0, 1, 1, 3, 3, 5, 6] // union(3, 4) 이후
[0, 1, 1, 3, 3, 1, 6] // union(1, 5) 이후
[0, 1, 1, 1, 3, 1, 6] // union(3, 5) 이후
여기서 parent 배열은 각 요소가 속한 그룹의 대표를 저장해요. 예를 들어, parent[1]은 1번 요소의 대표가 누구인지를 나타내요.
하지만 이 방법은 시간이 오래 걸릴 수 있어요. 예를 들어, find 함수를 반복해서 호출하면, 트리의 높이가 높아져서 시간이 더 걸릴 수 있어요. 이를 해결하기 위한 두 가지 방법이 있어요:
- 경로 압축(Path Compression)
- rank(트리의 높이) 사용하기
그림으로도 살펴보면 다음과 같아요.
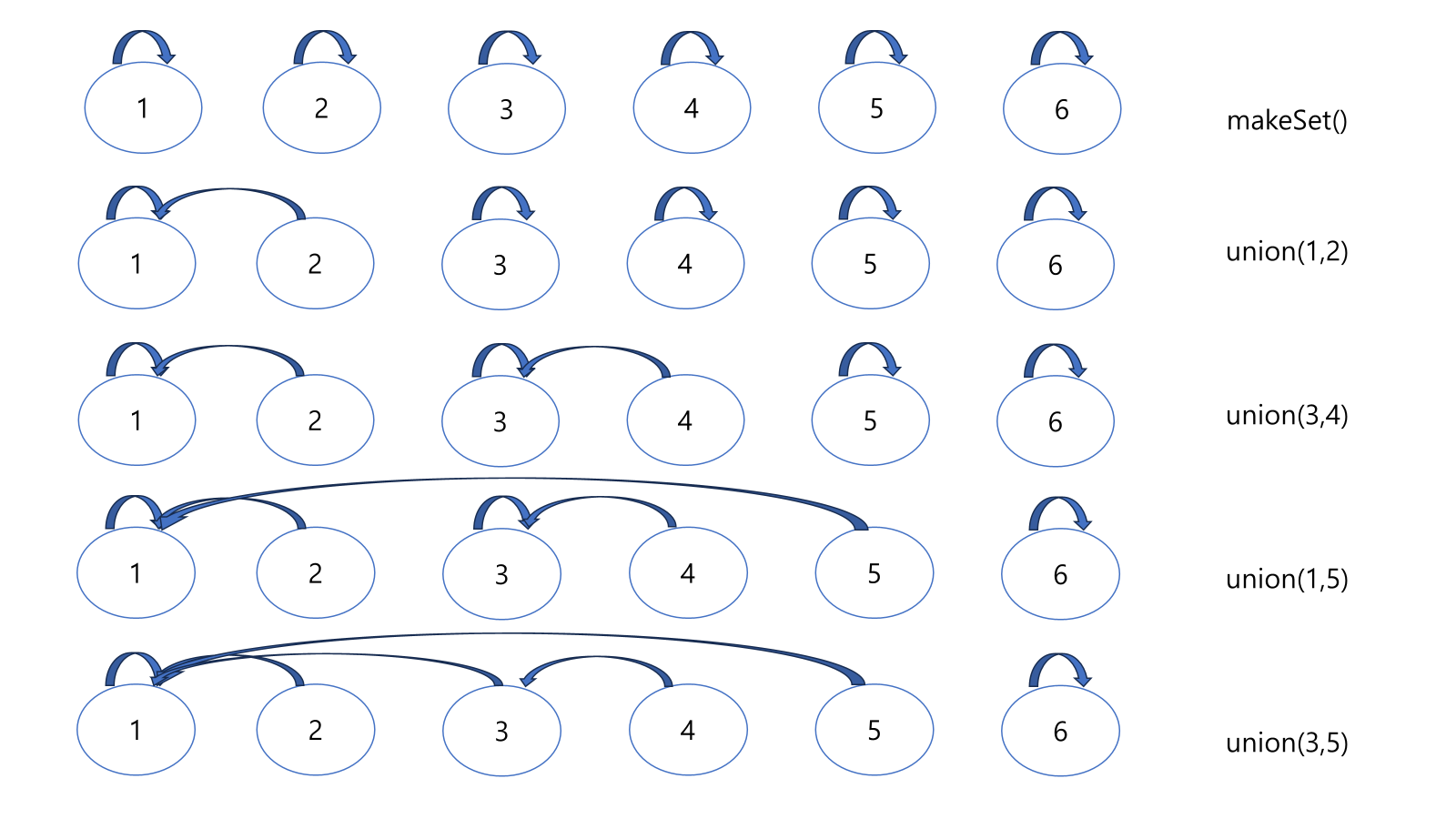
이 때 마지막 줄에서 1, 2, 3, 4, 5 를 따로 트리 형식으로 표현해봤어요.
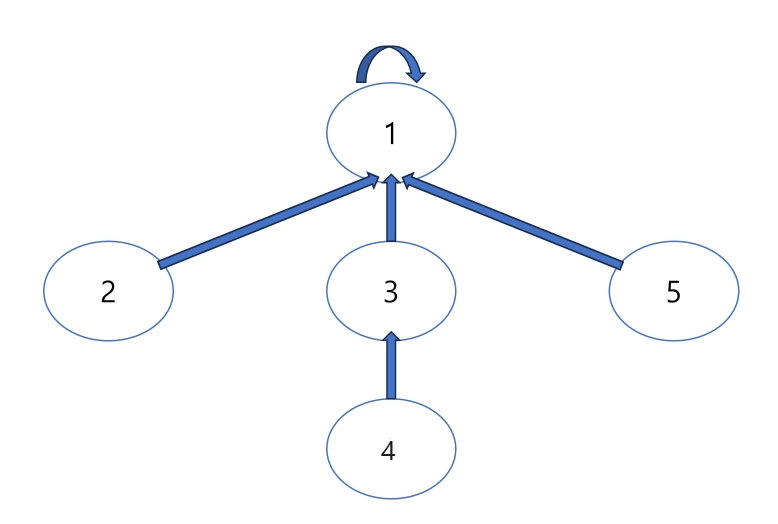
예를 들어, 4번 원소가 있어요. 4번 원소가 속한 집합의 대표 원소(루트)는 1번이에요. 하지만 처음에는 4번 원소가 3번을 대표로 알고 있어요. 그래서 find(4)를 하면 4에서 3으로, 그리고 다시 3에서 1로 이동해야 1번을 찾을 수 있어요.
만약 find(4)를 반복해서 호출한다고 생각해보세요. 매번 이렇게 4번이 3번을 거쳐 1번으로 가는 과정을 반복하게 돼요. 그러면 시간이 오래 걸리겠죠?
이 문제를 해결하려면 경로 압축을 사용해요. find(4)를 할 때, 4번 원소가 바로 1번을 대표로 기억하도록 바꿔주면, 다음번에는 바로 1번을 찾을 수 있게 돼요. 이렇게 하면 부모를 찾는 시간이 줄어들고 더 효율적으로 동작하게 돼요!
이를 해결하는 2가지 방법이 있어요.
- find 메서드에서 경로 압축하기
- rank(트리의 높이) 값을 이용하여 트리를 낮게 유지하기
1. 경로 압축(Path Compression)
경로 압축은 find 함수를 사용할 때, 찾으면서 그 경로의 요소들을 모두 대표로 연결해주는 방법이에요. 예를 들어, 4번 요소가 3번을, 3번 요소가 1번을 대표로 가리킨다면, find(4)를 했을 때 4번도 1번을 직접 가리키도록 바꿔주는 거예요.
public static int find(int x) {
if (x == parent[x])
return x;
return parent[x] = find(parent[x]);
}
이렇게 수정하면, find 함수를 한 번 호출할 때마다 트리가 더 낮게 유지되면서 빠르게 대표를 찾을 수 있어요!
2. rank 버전
rank는 트리의 높이를 관리하는 값이에요. 높이가 낮은 트리를 높이가 높은 트리에 붙여서 트리의 높이를 최대한 낮게 유지하는 방법이에요. 트리의 높이가 낮으면, 나중에 find 함수를 호출할 때 더 빨리 대표를 찾을 수 있겠죠?
public static void union(int x, int y) {
x = find(x);
y = find(y);
if (x != y) {
if (rank[x] < rank[y]) {
parent[x] = y;
} else if (rank[x] > rank[y]) {
parent[y] = x;
} else {
parent[y] = x;
rank[x]++;
}
}
}
이 코드에서는 rank를 사용해서 트리의 높이를 관리해요. 만약 두 트리의 높이가 같으면, 임의로 한쪽에 붙이고 rank 값을 +1 해줘요.
정리
서로소 집합(Disjoint Set) 알고리즘과 Union-Find는 서로 연결된 그룹을 빠르게 찾고 합칠 수 있는 방법이에요. 특히, 경로 압축과 rank를 사용하면 성능을 훨씬 더 빠르게 할 수 있어요. 이 알고리즘은 최소 신장 트리(MST)를 찾을 때도 자주 사용되니 기억해두면 좋아요!
