DFS 완전 정복 - I

이강용·2023년 11월 8일

목록 보기

4/14

DFS(Depth First Sarch)란?

깊이 우선 탐색
그래프 탐색 알고리즘
그래프 : 정점과 간선으로 이루어진 자료구조
정점(node) ❍
간선(edge) -

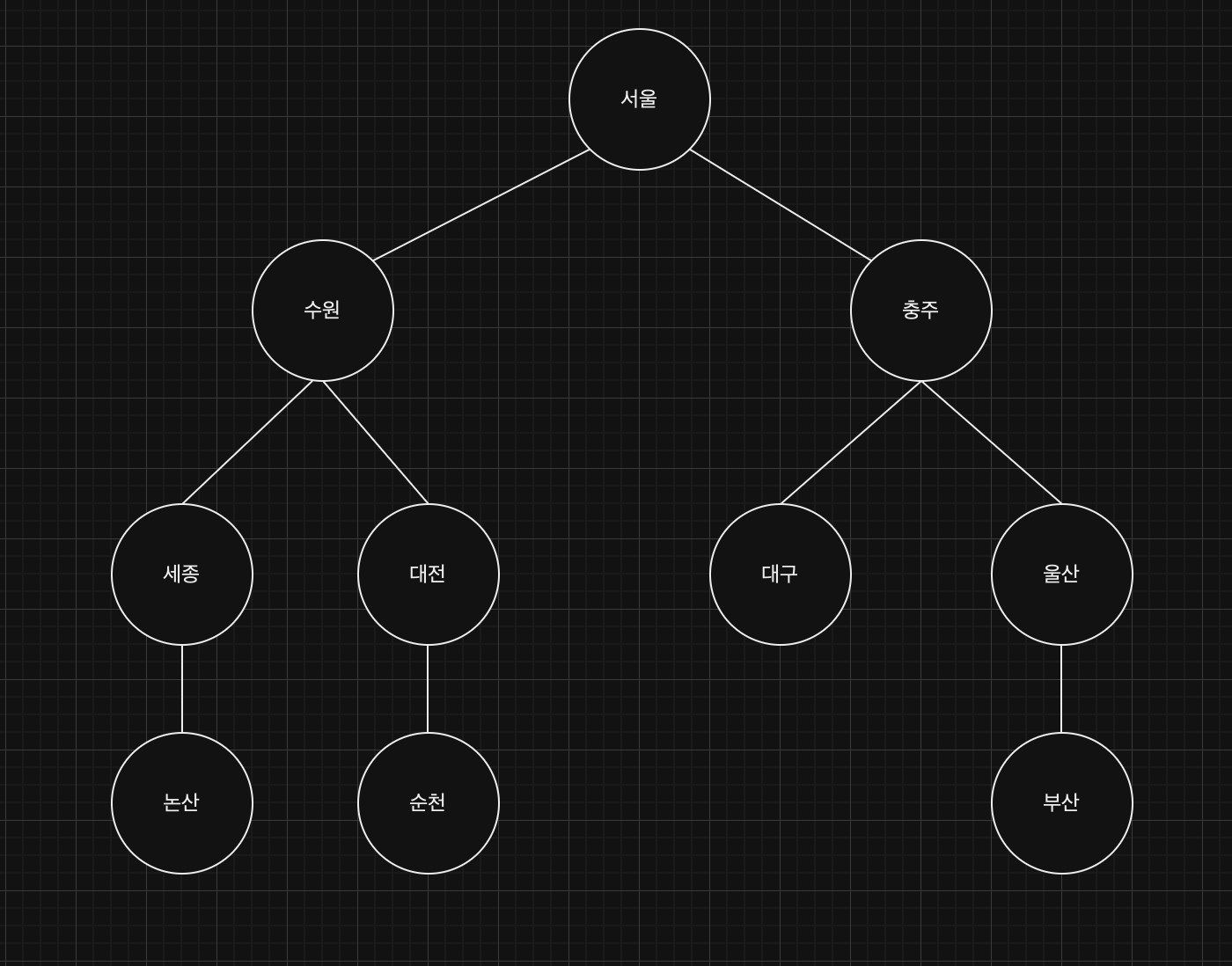
1. 서울
2. 수원
3. 세종
4. 논산
5. 대전
6. 순천
7. 충주
8. 대구
9. 울산
10. 부산

BFS(Breadth First Search)란?

너비 우선 탐색

1. 서울
2. 수원
3. 충주
4. 세종
5. 대전
6. 대구
7. 울산
8. 논산
9. 순천
10. 부산

백준 2606 바이러스

문) 신종 바이러스인 웜 바이러스는 네트워크를 통해 전파된다. 한 컴퓨터가 웜 바이러스에 걸리면 그 컴퓨터와 네트워크 상에서 연결되어 있는 모든 컴퓨터는 웜 바이러스에 걸리게 된다.

예를들어 7개의 컴퓨터가 <그림1>과 같이 네트워크 상에서 연결되어 있다고 하자. 1번 컴퓨터가 웜 바이러스에 걸리면 웜 바이러스는 2번과 5번 컴퓨터를 거쳐 3번과 6번 컴퓨터까지 전파되어 2,3,5,6 네 대의 컴퓨터는 웜 바이러스에 걸리게 된다. 하지만 4번과 7번 컴퓨터는 1번 컴퓨터와 네트워크상에서 연결되어 있지 않기 때문에 영향을 받지 않는다.

N : 컴퓨터의 수 (5 <= N <= 100)

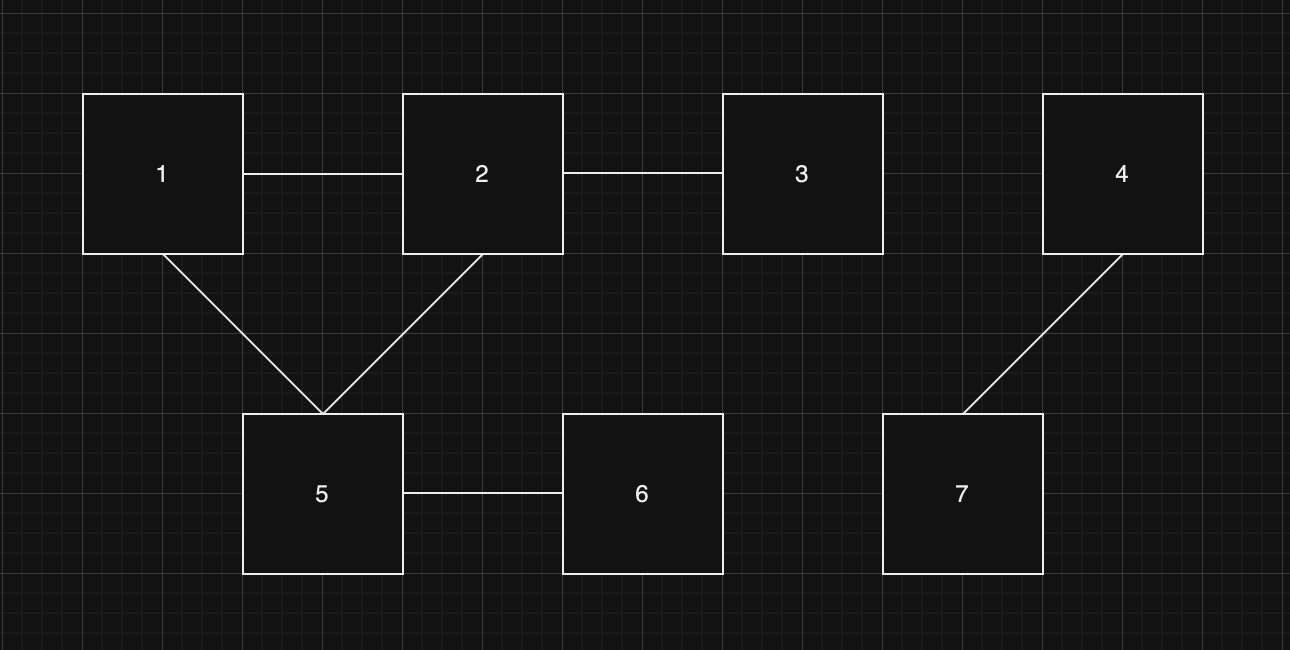
N	M
7	6

M개의 간선 정보

A	B
1	2
2	3
1	5
5	2
5	6
4	7

graph	1	2	3	4	5	6	7
0
1		T			T
2	T		T		T
3		T
4							T
5	T	T				T
6					T
7				T

visited

0	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0

풀이

package programmers;

public class Virus {
	
	static boolean[][] graph;
	static boolean[] visited;
	static int answer;
	
	
	public static void dfs(int idx, int N ) {
		visited[idx] = true;
		answer++;
		
		for(int i = 1; i <= N; i++) {
			if(visited[i] == false && graph[idx][i]) {
				dfs(i,N);				
			}
		}
		
	}
	
	public static int solution(int N, int M, int[][] connections) {
		
		graph = new boolean[N+1][N+1];
		visited = new boolean[N+1];
		answer = 0;
		
		for(int i = 0; i < M; i++) {
			int x = connections[i][0];
			int y = connections[i][1];
			graph[x][y] = true;
			graph[y][x] = true; 
		}
		dfs(1,N);
		return answer - 1;
	}
	public static void main(String[] args) {
		
		int[][] connections = {{1, 2}, {2, 3}, {1, 5}, {5, 2}, {5, 6}, {4, 7}};
		solution(7, 6, connections);
	}
}

네트워크 상에서 연결 -> DFS / BFS
서로 연결되었다는 정보를 어떻게 하나의 자료구조로 통합할까?
이미 방문한 지점을 다시 방문하지 않으려면 어떤 자료구조를 사용해야 될까?

백준 11724 연결 요소의 개수

문) 방향 없는 그래프가 주어졌을 때, 연결 요소(Connected Component)의 개수를 구하는 프로그램을 작성하시오.

N: 요소의 개수(5 <= N <= 1,000)

N	M
6	5

M개의 간선 정보

A	B
1	2
2	5
5	1
3	4
4	6

graph	1	2	3	4	5	6
0
1		T			T
2	T				T
3				T
4			T			T
5	T	T
6				T

visited

0	1	2	3	4	5	6
0	0	0	0	0	0	0

나의 풀이

package programmers;

public class NumOfConnectionElements {
	
	final static int MAX = 1000 + 10;
	static boolean[][] graph;
	static boolean[] visited;
	static int answer;
	
	public static void dfs(int idx, int N ) {
		
		visited[idx] = true;
		
		for(int i = 1; i <= N; i++) {
			if(visited[i] == false && graph[idx][i]) {
				dfs(i,N);
			}
		}
		
		
	}
	
	public static int solution(int N, int M, int[][] connections) {
		
		graph = new boolean[MAX][MAX];
		visited = new boolean[MAX];
		answer = 0;
		
		for(int i = 0; i < M; i++) {
			int x = connections[i][0];
			int y = connections[i][1];
			graph[x][y] = true;
			graph[y][x] = true; 
		}
		for(int i = 1; i <= N; i++) {
			if(visited[i] == false) {
				dfs(i,N);
				answer++;
			}
		}
		System.out.println(answer);
		return answer;
	}
	public static void main(String[] args) {
		
		int[][] connections = {{1, 2}, {2, 5}, {5, 1}, {3, 4}, {4, 6}};
		solution(6, 5, connections);
	}

}

정리

1.연결된 요소의 개수 -> DFS / BFS
2. 서로 연결되었다는 정보를 어떻게 하나의 자료구조로 통합할까?
3. 이미 방문한 지점을 다시 방문하지 않으려면 어떤 자료구조를 사용해야야 될까?
4. 어디에서 DFS를 시작할 것인가?

백준 24479

문) N개의 정점과 M개의 간선으로 구성된 무방향 그래프(undirected graph)가 주어진다. 정점 번호는 1번부터 N번이고 모든 간선의 가중치는 1이다. 정점 R에서 시작하여 깊이 우선 탐색으로 노드를 방문할 경우 노드의 방문 순서를 출력하자. 인접 정점은 오름차순으로 방문한다.

제한사항

정점의 수 N (5 <= N <= 100,000)
간선의 수 M (1 <= M <= 200,000)
시작 정점 R (1 <= R <= N)

N	M
5	5	1

M개의 간선 정보

A	B
1	4
1	2
2	3
2	4
3	4

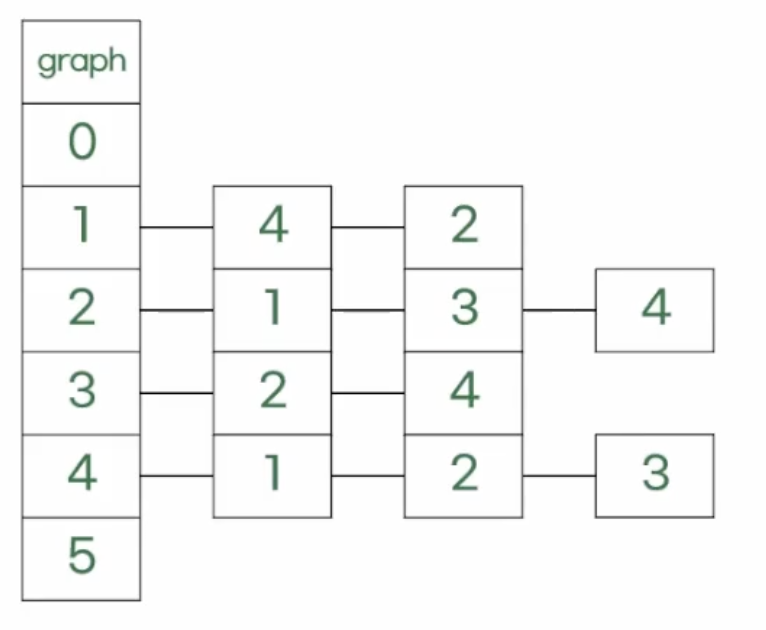
visited

0	1	2	3	4	5
0	0	0	0	0	0

answer

0	1	2	3	4	5
0	0	0	0	0	0

visited[1] = true, answer[1] = 1, 1 -> 2
visited[2] = true, answer[2] = 2, 2 -> 3
visited[3] = true, answer[3] = 3, 3 -> 4
visited[4] = true, answer[4] = 4

나의 풀이

package programmers;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;

public class Dfs1 {
	
	final static int MAX = 1000000 + 10;
	static ArrayList<Integer>[] graph;
	static boolean[] visited;
	static int[] answer;
	static int order;
	
	public static void dfs(int idx, int N ) {
		
		visited[idx] = true;
		answer[idx] = order;
		order++;
		
		for(int i = 0; i < graph[idx].size(); i++) {
			int next = graph[idx].get(i);
			if(visited[next] == false) {
				dfs(next,N);				
			}
		}
		
		
		
	}
	
	public static int[] solution(int N, int M, int R, int[][] connections) {
		
		graph = new ArrayList[MAX];
		for(int i = 1; i <= N; i++) {
			graph[i] = new ArrayList<>();
		}
		visited = new boolean[MAX];
		answer = new int[MAX];
		order = 1;
		
		for(int i = 0; i < M; i++) {
			int x = connections[i][0];
			int y = connections[i][1];
			graph[x].add(y);
			graph[y].add(x);
			
		}
		
		for(int i = 1; i <= N; i++) {
			Collections.sort(graph[i]);
		}
		
		dfs(R,N);
		
		
		return answer;
	}
	public static void main(String[] args) {
		
		int[][] connections = {{1, 4}, {1, 2}, {2, 3}, {2, 4}, {3, 4}};
		solution(5, 5, 1, connections);
	}

}

정리

1. DFS, 정점, 간선, 무방향 그래프 -> DFS / BFS
2. 서로 연결되었다는 정보를 어떻게 하나의 자료구조로 통합할까?
-  2차원 배열 vs ArrayList
3. 이미 방문한 지점을 다시 방문하지 않으려면 어떤 자료구조를 사용해야야 될까?
4. 어떻게 오름차순으로 방문할 수 있을까?
5. 방문 순서를 담기 위해서는 어떤 자료구조를 사용해야 될까?

백준 24480

문) N개의 정점과 M개의 간선으로 구성된 무방향 그래프(undirected graph)가 주어진다. 정점 번호는 1번부터 N번이고 모든 간선의 가중치는 1이다. 정점 R에서 시작하여 깊이 우선 탐색으로 노드를 방문할 경우 노드의 방문순서를 출력하자. 인접 정점은 내림차순으로 방문한다.

제한사항

정점의 수 N (5 <= N <= 100,000)
간선의 수 M (1 <= M <= 200,000)
시작 정점 R (1 <= R <= N)

N	M
5	5	1

M개의 간선 정보

A	B
1	4
1	2
2	3
2	4
3	4

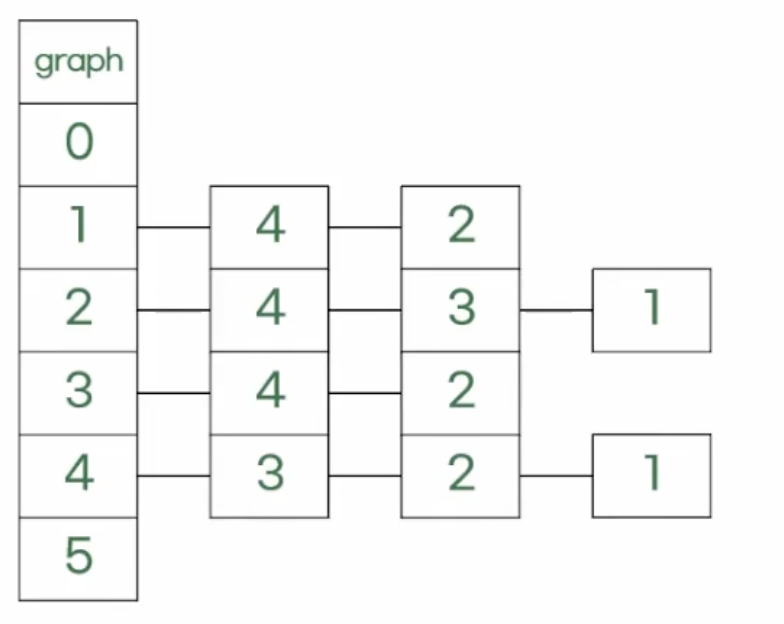
visited[1] = true, answer[1] = 1, 1 -> 4
visited[4] = true, answer[4] = 2, 2 -> 3
visited[3] = true, answer[3] = 3, 3 -> 2
visited[2] = true, answer[2] = 4

나의 풀이

package programmers;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;

public class Dfs2 {
	
	final static int MAX = 1000000 + 10;
	static ArrayList<Integer>[] graph;
	static boolean[] visited;
	static int[] answer;
	static int order;
	
	public static void dfs(int idx, int N ) {
		
		visited[idx] = true;
		answer[idx] = order;
		order++;
		
		for(int i = 0; i < graph[idx].size(); i++) {
			int next = graph[idx].get(i);
			if(visited[next] == false) {
				dfs(next,N);				
			}
		}
		
		
		
	}
	
	public static int[] solution(int N, int M, int R, int[][] connections) {
		
		graph = new ArrayList[MAX];
		for(int i = 1; i <= N; i++) {
			graph[i] = new ArrayList<>();
		}
		visited = new boolean[MAX];
		answer = new int[MAX];
		order = 1;
		
		for(int i = 0; i < M; i++) {
			int x = connections[i][0];
			int y = connections[i][1];
			graph[x].add(y);
			graph[y].add(x);
			
		}
		
		
		for(int i = 1; i <= N; i++) {
			Collections.sort(graph[i], Collections.reverseOrder());
		}
		
		dfs(R,N);
		
		System.out.println(Arrays.toString(answer));
		return answer;
	}
	public static void main(String[] args) {
		
		int[][] connections = {{1, 4}, {1, 2}, {2, 3}, {2, 4}, {3, 4}};
		solution(5, 5, 1, connections);
	}

}

백준 1260

문) 그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 없는 점이 없는 경우 종료한다.

정점번호는 1번부터 N번까지이다.

제한사항

정점의 수 N (1 <= N <= 1,000)
간선의 수 M (1 <= M <= 1,000)

DFS 풀이

N	4
M	5
V	1

M개의 간선 정보

1	2
1	3
1	4
2	4
3	4

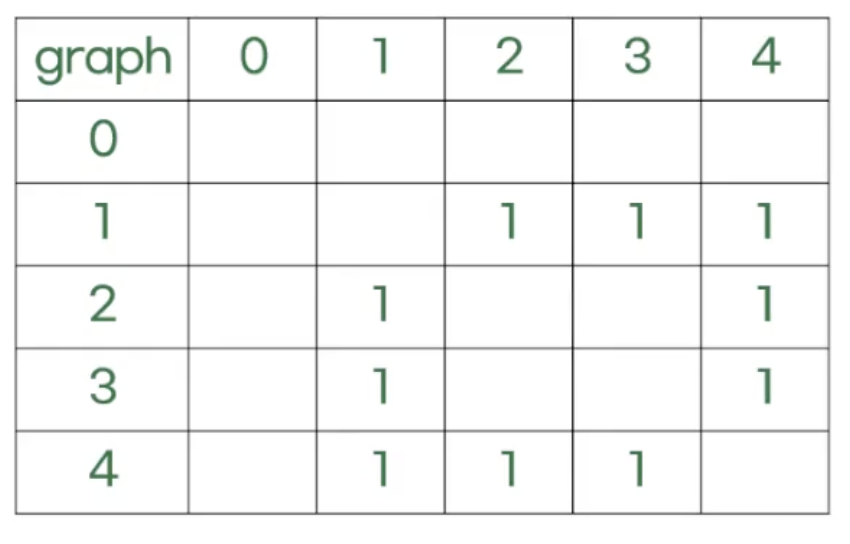
BFS 풀이

N	4
M	5
V	1

M개의 간선 정보

1	2
1	3
1	4
2	4
3	4

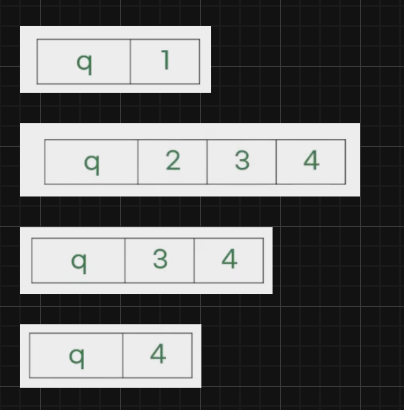
풀이

package programmers;

import java.util.ArrayList;
import java.util.Arrays;

public class Dfs3 {
	
	final static int MAX = 1000 + 10;
	static boolean graph[][];
	static boolean visited[];
	static ArrayList<Integer> queue; //BFS
	
	
	public static void dfs(int idx, int N) {
		visited[idx] = true;
		System.out.print(idx + " ");
		
		for(int i = 1; i <= N; i++) {
			if(visited[i] == false && graph[idx][i] == true ) {
				dfs(i, N);
			}
		}
		
	}
	
	public static void bfs(int V, int N) {
		queue = new ArrayList<>();
		visited = new boolean[MAX];
		
		queue.add(V);
		visited[V] = true;
		
		while(!queue.isEmpty()) {
			int idx = queue.remove(0);
			System.out.print(idx + " ");
			
			for(int i = 1; i <= N; i++) {
				if(visited[i] == false && graph[idx][i] == true) {
					queue.add(i);
					visited[i] = true;					
				}
			}
		}
		
	}
	
	public static void solution(int N, int M, int V, int[][] connections) {
		
		
		graph = new boolean[MAX][MAX];
		visited = new boolean[MAX];
		
		for(int i = 0; i < M; i++) {
			int x = connections[i][0];
			int y = connections[i][1];
			
			graph[x][y] = true;
			graph[y][x] = true;
			
		}
		
		dfs(V,N);
		System.out.println();
		
		bfs(V,N);
		
		
	}
	public static void main(String[] args) {
		
		int[][] connections = {{1, 2}, {1, 3}, {1, 4}, {2, 4}, {3, 4}};
		solution(4, 5, 1, connections);
	}
}

정리

1. DFS, BFS 방문 순서 => DFS/BFS

  for(int i = 1; i <= N; i++) {

  }

2. 서로 연결되었다는 정보를 어떻게 하나의 자료구조로 통합할까?

- 2차원 배열 Vs ArrayList

3. 어떻게 오름차순으로 방문할 수 있을까?

    for(int i = 1; i <= N; i++) {

    }

4. 이미 방문한 지점을 다시 방문하지 않으려면 어떤 자료구조를 사용해야 할까?

백준 2644

문) 우리 나라는 가족 혹은 친척들 사이의 관계를 촌수라는 단위로 표현하는 독특한 문화를 가지고 있다. 이러한 촌수는 다음과 같은 방식으로 계산된다. 기본적으로 부모와 자식 사이를 1촌으로 정의하고 이로부터 사람들 간의 촌수를 계산한다. 예를들면 나와 아버지, 아버지와 할아버지는 각각 1촌으로 나와 할아버지는 2촌이 되고, 아버지 형제들과 할아버지는 1촌, 나와 아버지 형제들과는 3촌이 된다.
여러 사람들에 대한 부모 자식들 간의 관계가 주어졌을 때, 주어진 두 사람의 촌수를 계산하는 프로그램을 작성하시오.

정점번호는 1번부터 N번까지이다.

N : (1 <= N <= 100)
M : 부모 자식들 간의 관계의 개수

풀이 개념 설명

N	9
start	7
end	3
M	7

M개의 간선 정보

1	2
1	3
2	7
2	8
2	9
4	5
4	6

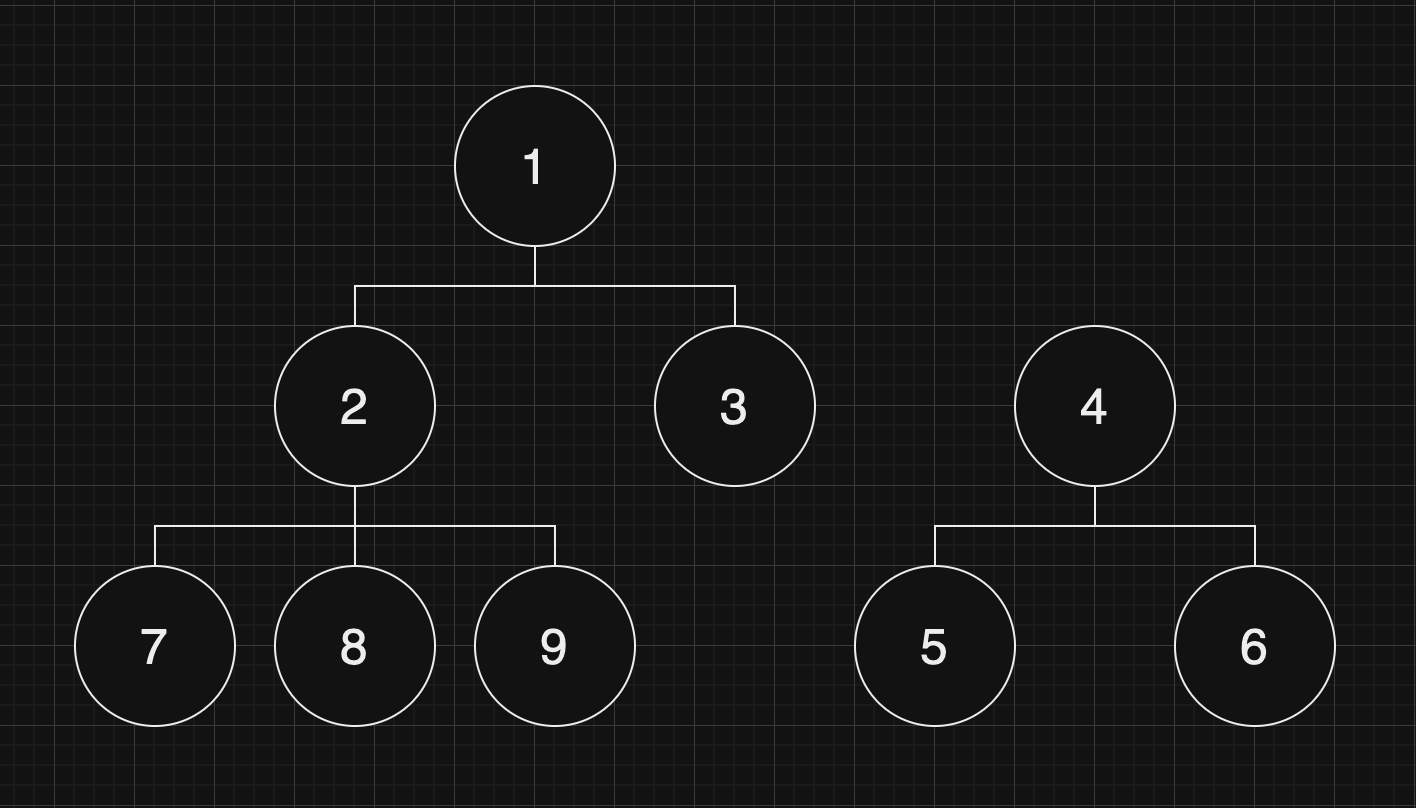
start: 7 

visited[7] = true;
7번에서 연결된 가장 작은 Node(2) 방문
visited[2] = true;
2와 end(3)이 같나? -> NO
2번에서 연결된 가장 작은 Node(1) 방문
visited[1] = true;
1과 end(3)이 같나? -> NO
1번에서 연결된 가장 작은 Node(3) 방문
3과 end(3)이 같나? -> YES

나의 풀이

package programmers;

public class FindARelative {
	
	final static int MAX = 100 + 10;
	static boolean[][] graph;
	static boolean[] visited;
	static int answer;
	
	public static void dfs(int idx, int end, int N, int relation) {
		visited[idx] = true;
		
	    
		if(idx == end) {
			answer = relation;
			return;
		}
		
		
		for(int i = 1; i <= N; i++) {
			
			if(!visited[i] && graph[idx][i]) {
				dfs(i, end, N, relation + 1);
				if (answer != -1) {
					return;
				}
			}
			
		}
		
	}
	
	
	
	public static int solution(int N, int start, int end, int M, int[][] connections) {
		
		graph = new boolean[MAX][MAX];
		visited = new boolean[MAX];
		answer = -1;
		
		for(int i = 0; i < M; i++) {
			int x = connections[i][0];
			int y = connections[i][1];
			
			graph[x][y] = true;
			graph[y][x] = true;
			
		}
		
		dfs(start, end, N, 0);
		
		
		System.out.println(answer);
		return answer;
	}
	public static void main(String[] args) {
		
		int[][] connections = {{1, 2}, {1, 3}, {2, 7}, {2, 8}, {2, 9}, {4, 5}, {4, 6}};
		solution(9, 7, 3, 7, connections);
	}

}

백준 11725

문) 루트 없는 트리가 주어진다. 이때, 트리의 루트를 1이라고 정했을 때, 각 노드의 부모를 구하는 프로그램을 작성하시오.

N : 노드의 개수 ( 2 <= N <= 100,000)

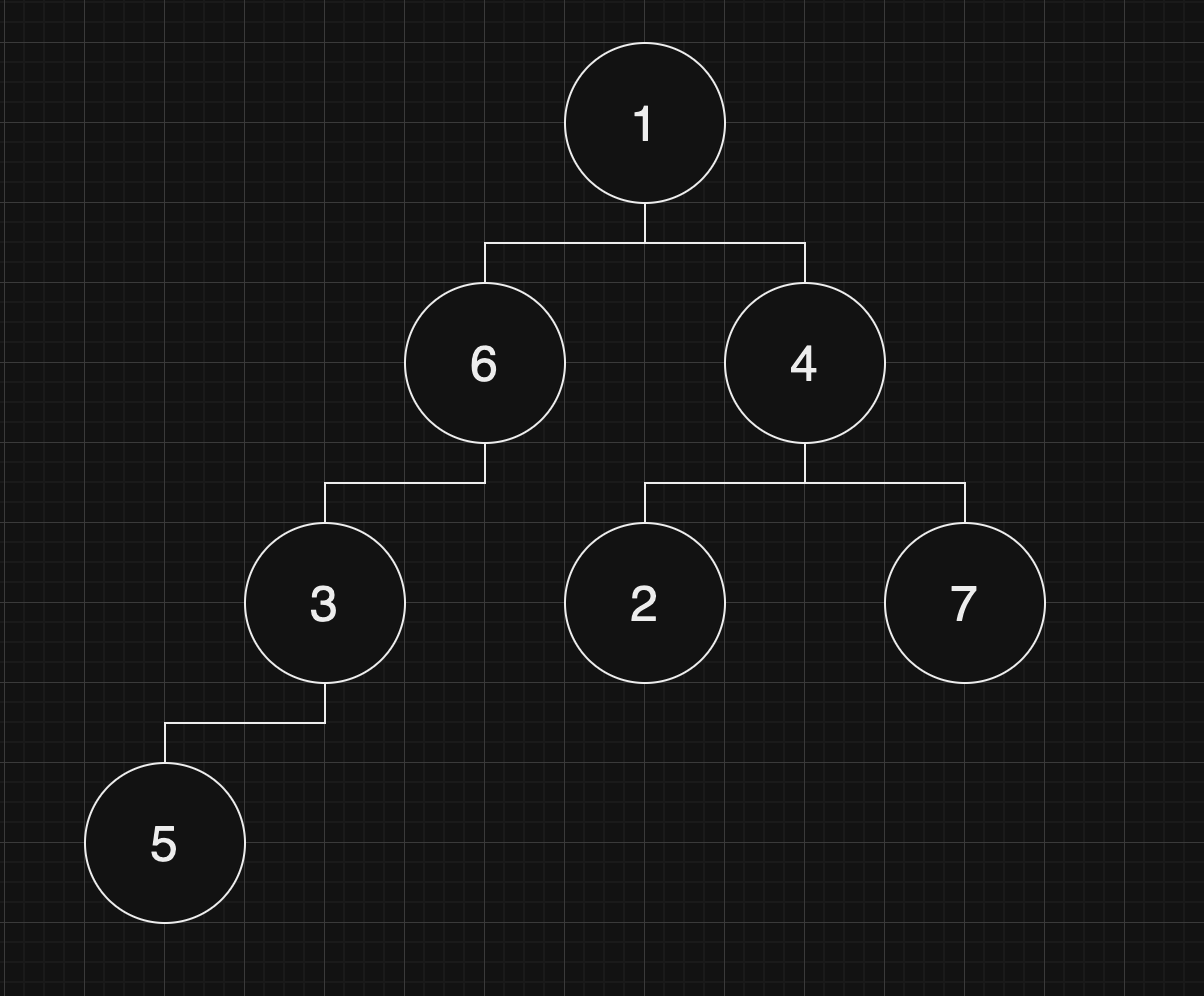
문제 설명 및 풀이

N	7

간선 정보

1	6
6	3
3	5
4	1
2	4
4	7

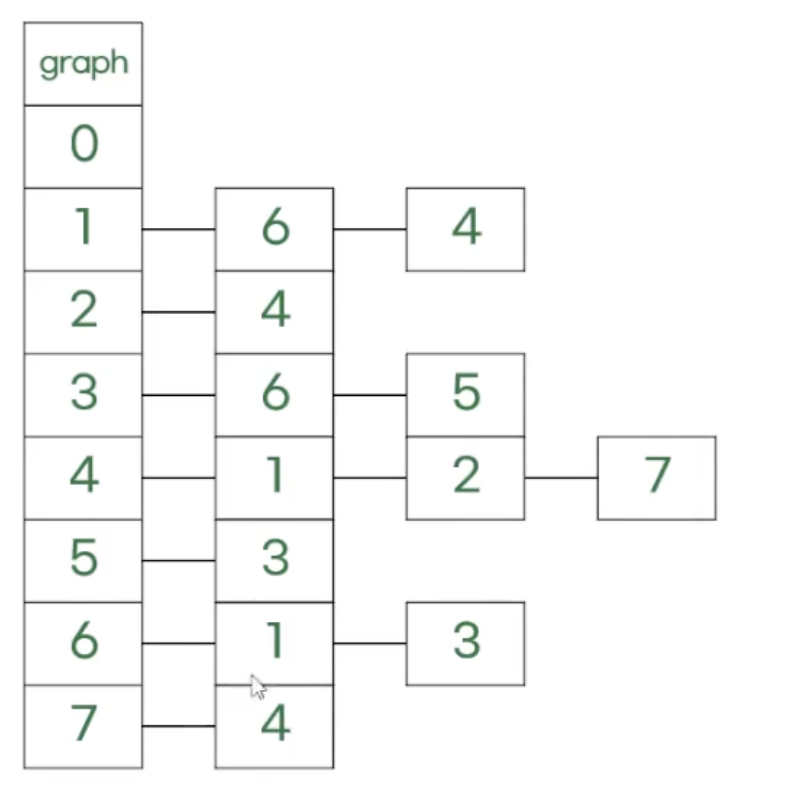
visited	0	1	2	3	4	5	6	7
	0	1	1	1	1	1	1	1

answer	0	1	2	3	4	5	6	7
	0	0	4	6	1	3	1	4

나의 풀이

package programmers;

import java.util.ArrayList;
import java.util.Arrays;

public class Dfs4 {
	
	final static int MAX = 100000 + 10;
	static ArrayList<Integer> [] graph;
	static boolean[] visited;
	static int[] myParents;
	
	public static int[] dfs(int idx) {
		visited[idx] = true;
	
		for(int i = 0; i < graph[idx].size(); i++) {
			int next = graph[idx].get(i);
			
			if(!visited[next]) {
				myParents[next] = idx;
				dfs(next);
			}
		}
		return myParents;
	}
	
	
	public static int[] solution(int N, int[][] connections) {
		
		graph = new ArrayList[MAX];
		
		for(int i = 0; i <= N; i++) {
			graph[i] = new ArrayList<>();
		}
		
		visited = new boolean[MAX];
		myParents = new int[MAX];
		
		for(int i = 0;  i < N - 1; i++) {
			int x = connections[i][0];
			int y = connections[i][1];
			
			graph[x].add(y);
			graph[y].add(x);
		}
		
		dfs(1);
		int[] answer = new int[N-1];
		for(int i = 2; i <= N; i++) {
			answer[i - 2] = myParents[i];
		}
		
		System.out.println(Arrays.toString(answer));
		return answer;
	}
	public static void main(String[] args) {
		
		int[][] connections = {{1, 6}, {6, 3}, {3, 5}, {4, 1}, {2, 4}, {4, 7}};
		solution(7, connections);
	}

}

/*
	 * idx = 1, visited[1] = true, next = 6, myParents[6] = 1, dfs(6)
	 * idx = 6, visited[6] = true, next = 3, myParents[3] = 6, dfs(3)
	 * idx = 3, visited[3] = true, next = 5, myParents[5] = 3, dfs(5)
	 * idx = 5, visited[5] = true, no unvisited children, return to idx = 3
	 * idx = 3, visited[3] = true, all children visited, return to idx = 6
	 * idx = 6, visited[6] = true, next = 1, 1 is root and already visited, skip to next child
	 * idx = 6, visited[6] = true, all children visited, return to idx = 1
	 * idx = 1, visited[1] = true, next = 4, myParents[4] = 1, dfs(4)
	 * idx = 4, visited[4] = true, next = 2, myParents[2] = 4, dfs(2)
	 * idx = 2, visited[2] = true, no unvisited children, return to idx = 4
	 * idx = 4, visited[4] = true, next = 7, myParents[7] = 4, dfs(7)
	 * idx = 7, visited[7] = true, no unvisited children, return to idx = 4
	 * idx = 4, visited[4] = true, all children visited, return to idx = 1
	 * idx = 1, visited[1] = true, all children visited, DFS complete
	 * */