알고리즘 문제를 풀다가 재귀호출에 관한 문제를 풀다가 작성한 블로그 내용이 있다.
하지만, 알고리즘 - 재귀 호출 1탄 23년 4월 이후 재귀 호출에 관한 공부가 미흡했는지, 알고리즘 문제를 풀면서 또 다시 이해가 안가는 부분이 있어서 추가 공부를 바탕으로 블로그 내용을 작성해보려고 한다.
재귀 관련 알고리즘 문제를 풀다보면 깊이 우선 탐색(DFS : Depth First Search)와 같은 용어를 접할 수 있는데, 이를 위해, 재귀의 방법 및 깊이 우선 탐색의 각 개념에 대해 짧게 알아보자.
-
상향식 분석 : 상향식 접근법은 작은 문제부터 시작하여 큰 문제로 확장하는 방식이며, 문제를 가장 작은 단위로 나눈 다음, 그 결과를 사용하여 상위 단계의 문제를 해결하는 방법이다. 주로
다이나믹 프로그래밍에서 주로 사용되는 방식이다. -
하향식 분석 : 재귀를 통해 문제를 작은 부분 문제로 나누어 해결하는 접근법으로, 문제의 크기나 복잡성을 줄여나가며, 기저 조건에 도달하면 재귀 호출을 멈추고 원래의 문제로 돌아와 해결을 하는 방법이다.
-
DFS ( Depth First Search) : 그래프나 트리와 같은 데이터 구조를 탐색할 때 사용하는 알고리즘 중 하나로 시작 노드에서 가능한 깊에 탐색하며, 더 이상 방문할 노드가 없으면 이전 노드로 돌아와 다음 경로를 탐색한다.
재귀의 하향식 분석과 DFS의 연관성 ?
-
DFS는 자연스럽게 재귀적으로 구현될 수 있다. 현재 노드에서 인접한 노드를 탐색할 때마다 그 노드에서 다시 DFS를 호출하게 된다. 이렇게 재귀적으로 노드를 방문하면서 깊이 우선으로 탐색을 진행한다.
-
재귀적으로 문제를 접근할 때 하향식으로 큰 문제를 작은 부분 문제로 분해하는 것과 유사하게, DFS에서는 현재 위치에서 가능한 방향으로 하향식으로 깊게 들어가 탐색함
-
재귀 호출은 내부적으로 시스템 스택을 사용하여 함수 호출의 정보를 저장하는데, DFS는 이와 유사하게 스택을 사용하여 방문한 노드와 그 노드에서의 탐색 상태를 저장하고 관리한다.
package programmers;
public class Recur {
public static void recur(int n) {
if(n > 0) {
recur(n - 1);
System.out.println(n);
recur(n - 2);
}
}
public static void main(String[] args) {
int n = 4;
recur(n);
}
}
위 로직을 실행했을 때 나오는 결과는 어떻게 나올까?
1
2
3
1
4
1
2문제를 구현하는 방법은 너무나 간단해보인다... 하지만 나는 로직을 보고 "뭐지...?" 라는 생각을 먼저했다.
recur(4) 호출
recur(3) 호출
4 출력
recur(2) 호출??? 나는 당연스럽게 4가 제일 처음 출력되는줄 알았지만

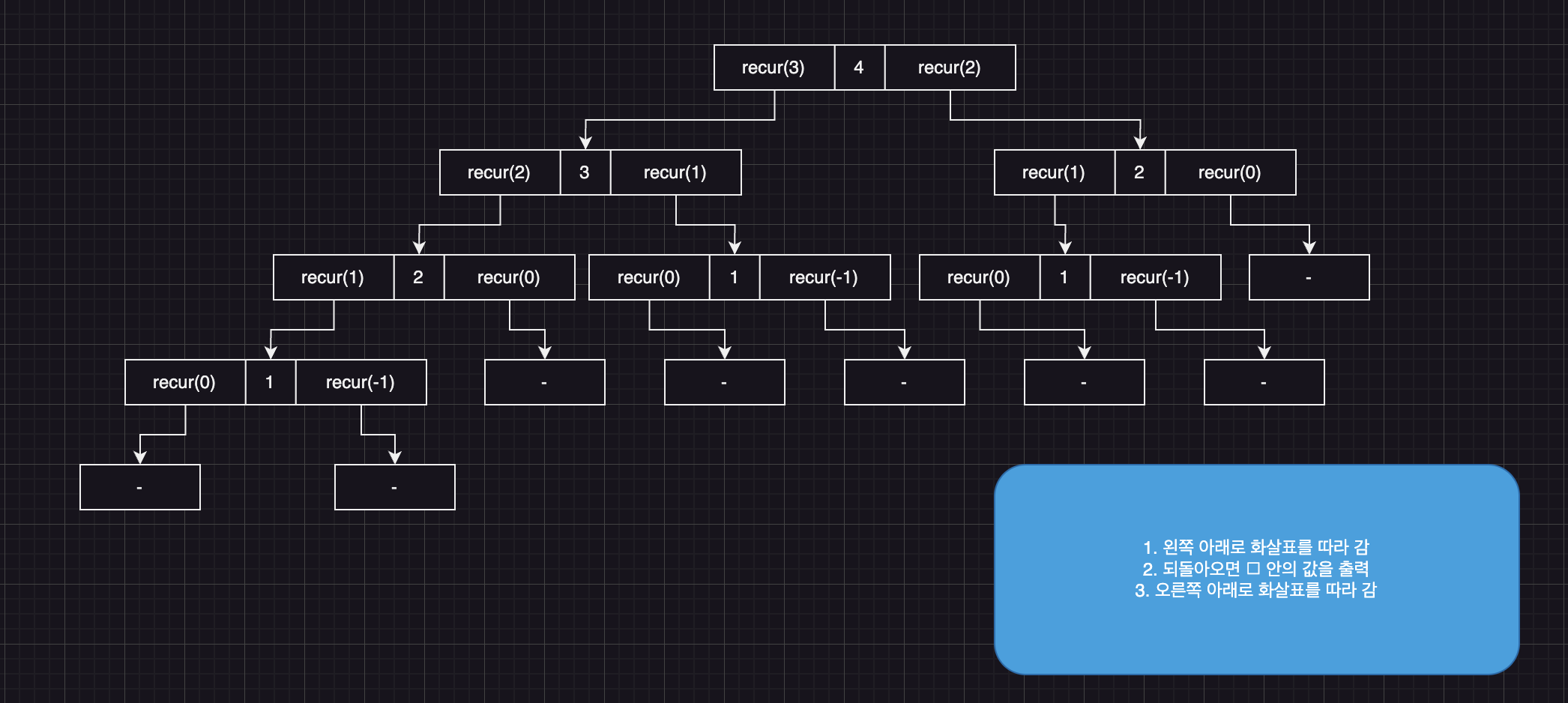
결과는 다음과 같은 순서로 출력되었다. 왜 이런 결과가 나오는지 그림을 보면서 설명하겠다.
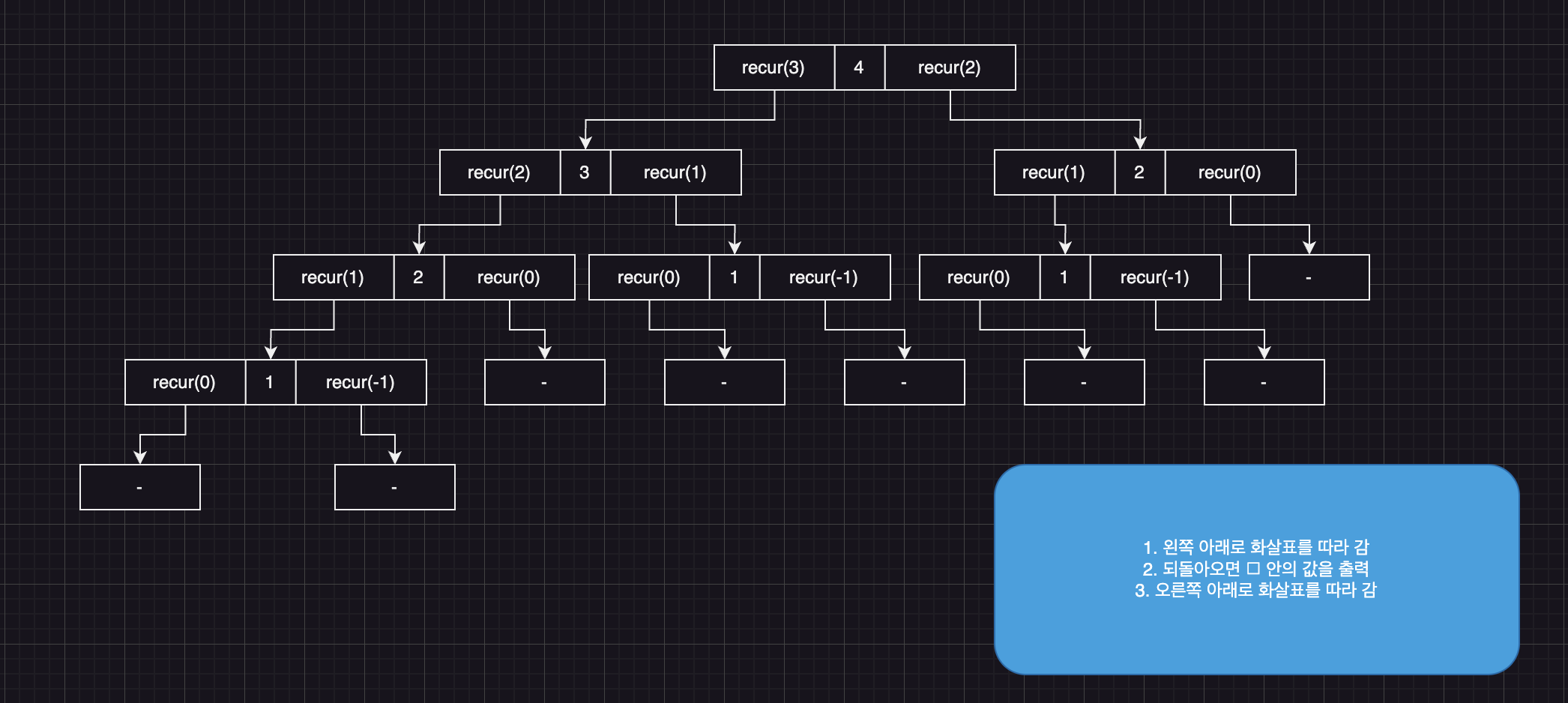
if(n > 0) {
recur(n - 1);
System.out.println(n);
recur(n - 2);
}즉, 해당 로직에서 출력문이 동작하려면 recur()호출문이 모두 동작하고 난 뒤 실행하되는 것이다. 따라서, 왼쪽 자식노드 부터 오른쪽 자식노드까지 순서대로 동작한다
Stack을 이용한 DFS 알고리즘
package programmers;
import java.util.Stack;
public class Recur {
public static void recur(int n) {
Stack<Integer> s = new Stack<>();
while(true) {
if(n > 0) {
s.push(n);
n = n - 1;
continue;
}
if(!s.isEmpty()) {
n = s.pop();
System.out.println(n);
n = n - 2;
continue;
}
break;
}
}
public static void main(String[] args) {
int n = 4;
recur(n);
}
}
동작 순서를 보면 다음과 같다.
n = 4
Stack s = []
1. n이 0보다 크므로, n값을 Stack에 push하고 n을 1 감소시킴
n = 3
Stack s = [4]
2. 동일한 조건에 따라, n값을 Stack에 push하고 n을 1 감소시킴
n = 2
Stack s = [4, 3]
3. 패턴을 반복
n = 1
Stack s = [4,3,2]
4.
n = 0
Stack s = [4,3,2,1]
5. n = 0 이므로 if문을 빠져나와 (continue) 다음 로직을 수행
Stack s의 최상단 값 1을 pop
n = -1 (1 - 2)
Stack s = [4,3,2]
출력 1
6. n이 0보다 작아지므로, 다시 Stack에서 pop
Stack s의 최상단 값 2를 pop
n = 0 (2 - 2)
Stack s = [4,3]
출력 2
7. n = 0 이므로, 다시 Stack에서 pop
Stack s의 최상단 값 3을 pop
n = 1 (3 - 2)
Stack s = [4]
출력 3
8. n > 0 므로, Stack에 Push
n = 0 (1 - 1)
Stack s = [4,1]
9. n = 0 이므로, Stack에서 pop
Stack s의 최상단 1을 pop
n = -1 (1 - 2)
Stack s = [4]
출력 1
10. n이 0보다 작으므로, stack에서 pop
Stack s의 최상단 4를 pop
n = 2 (4 - 2)
Stack s = []
출력 4
11. n > 0 므로, Stack에 push
n = 1 (2 - 1)
Stack s = [2]
12. n > 0 므로, Stack에 push
n = 0 (1 - 1)
Stack s = [2,1]
13. n = 0 므로 , Stack에서 pop
Stack s의 최상단 1을 pop
n = -1 (1 - 2)
Stack s = [2]
출력 1
14. n < 0 이므로, Stack에서 pop
Stack s의 최상단 2를 pop
n = 0 (2 - 2)
Stack s = []
출력 2
현재 n = 0이고, Stack이 비어있기때문에, break문으로 while문을 탈출
메모제이션(Memoization)을 사용한 방법
- 메모이제이션(
Memoization)은 동적 프로그래밍의 핵심 기술로, 이전에 계산한 값을 저장해 두고 같은 계산이 또 필요할 때 저장된 값을 재활용하는 최적화 기법이다. 메모이제이션은 재귀 함수나 반복문 등에서 계산의 중복을 방지하기 위해 사용된다.
피보나치 수열을 메모이제이션 기법을 적용해보자
public int fibonacci(int n){
if(n <= 1) return n;
return fibonacci(n-1) + fibonacci(n-2);
}메모이제이션을 적용한 피보나치
public class Main{
public static int[] memo;
public static int fibonacci(int n){
if(n <= 1) return n;
if(memo[n] != 0) return memo[n];
memo[n] = fibonacci(n-1) + fibonacci(n-2);
return memo[n];
}
public static void main(Stirng[] args){
int n = 10;
memo = new int[n + 1];
}
}