재귀 호출 이란?

• 재귀 호출(Recursion)은 자기 자신을 호출하는 함수를 뜻합니다. 이를 통해 복잡한 문제를 작은 문제로 나누어 해결하는 분할 정복(Divide and Conquer) 알고리즘 등에 활용됩니다. 재귀 호출은 종료 조건이 반드시 필요하며, 종료 조건을 만족하지 않으면 무한 반복에 빠질 수 있습니다.

팩토리얼을 구하는 재귀 함수

N! = N * (N - 1) * (N - 2) * ... * 2 * 1
= N * (N - 1)!, 단 0! = 1

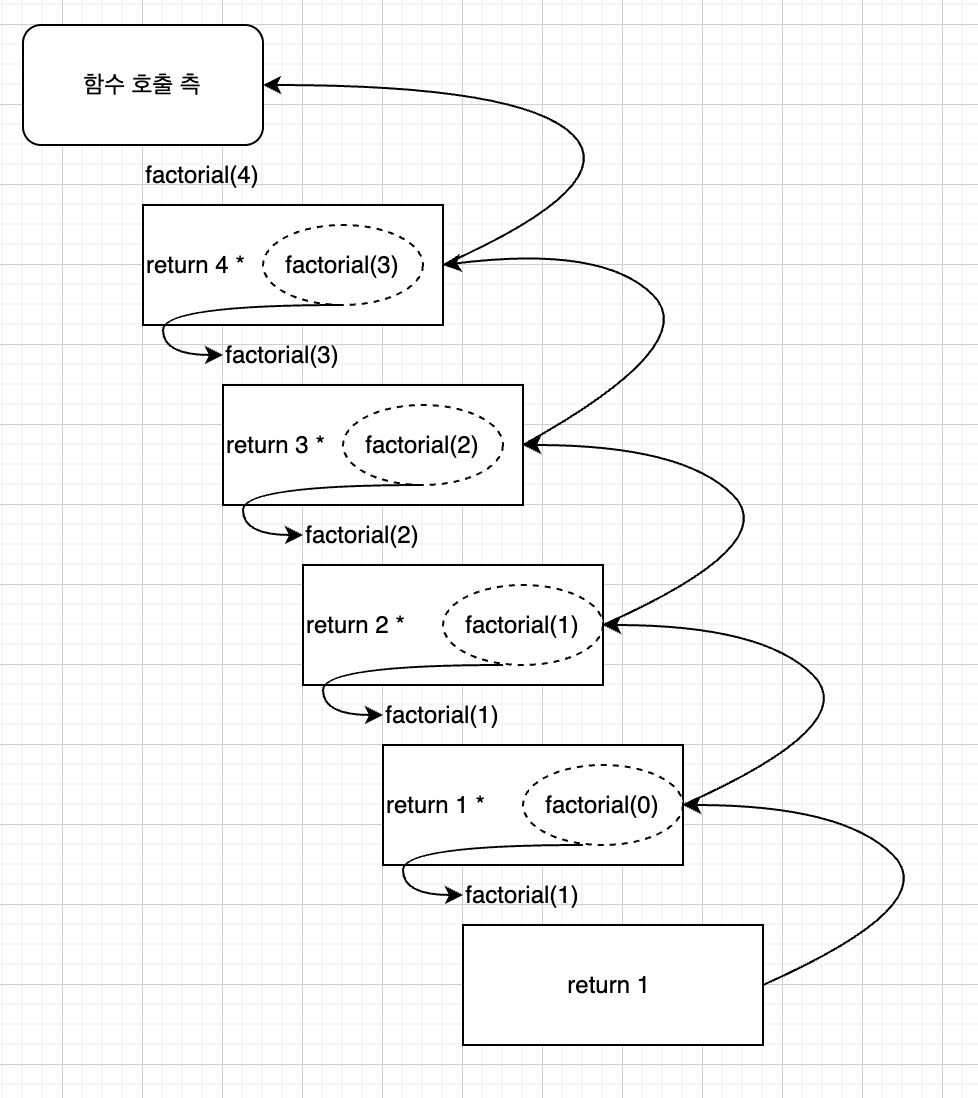
public static int factorial(int n) {
    if (n == 0) { // 종료 조건
        return 1;
    } else {
        return n * factorial(n-1); // 재귀 호출
    }
}

피보나치 수열을 구하는 재귀함수

재귀 호출은 한 함수 내에서 한번만 이루어져야 하는 것은 아니다. 한 함수 내에서도 두번 혹은 그 이상도 자기자신을 호출할 수 있다. 자기 호출 횟수는 주어진 문제를 몇 개로 나누어서 푸느냐에 따라 결정이 된다. 예를 들어 피보나치Fibonacci수열을 생각해보자. 피보나치 수열의 정의는 다음과 같다.

F[N] = F[N-1] + F[N-2] 단, F[1] = F[2] = 1

F[N]을 구하기 위해서는 재귀적인 호출이 F[N-1]을 알아야 할 뿐아니라 F[N-2]도 알아야 하므로 재귀 호출을 두 번해야 한다.

public static int fibonacci(int n) {
    if (n == 1 || n == 2) {
        return 1;
    } else {
        return fibonacci(n-1) + fibonacci(n-2);
    }
}

fibonacci()함수는 수식으로의 정의와 완전히 동일한 모양임을 알 수 있다. 일반적으로 재귀 호출이 두 번 이상 있을 때 재귀 호출을 분석하는 가장 정확하고 편한 방법은 재귀 나무 Recursive Tree를 만드는 것이다. 이는 재귀 함수가 호출이 되는 과정과 각 인자들을 정확히 보여준다.

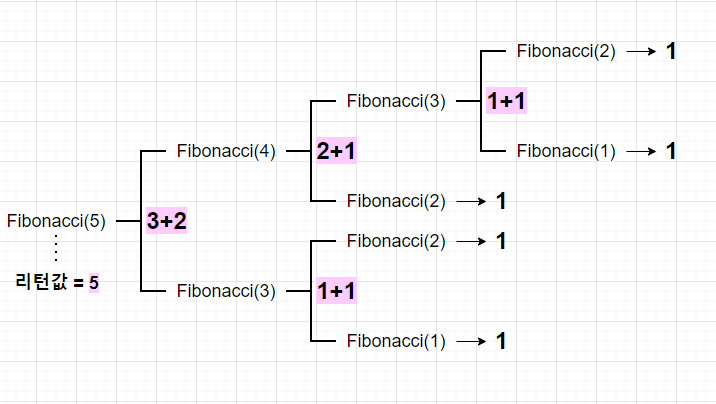
재귀 호출의 전략

1. 문제의 크기를 조금씩 줄여가는 방법
   • 너무 커서 해결이 힘든 문제는 해결할 수 있는 단위까지 차례로 줄여서 해결
   • factorial , fibonacci, 하노이탑
2. 문제의 크기를 양분하여 가는 방법
   • 꼭 절반이 아니라도 되는 경우가 있으며 (퀵 정렬), 수학적으로 정확히 반을 나누어가는 문제 유형을 분할해서 통치 (divide and conquer)라 한다.
3. 문제의 크기를 자르는 것이 아니라 문제 자체에 점근하여 가는 방법
   • 대표적인 예로 나무를 타는 방법preorder은 이진 트리 (binary tree)를 탐색하는 방법 중 하나이다. 이진 트리는 루트 노트 (root node), 왼쪽 자식 노드 (left child node), 오른쪽 자식 노드 (right child node)로 구성되어 있으며, 나무를 타는 방법은 다음과 같다.

1. 현재 노드를 방문한다.
2. 왼쪽 자식 노드를 방문한다.
3. 오른쪽 자식 노드를 방문한다.

이 방법을 재귀 호출로 구현하면 다음과 같다.

public static void preorder(Node node) {
    if (node != null) {
        visit(node); // 현재 노드를 방문한다.
        preorder(node.left); // 왼쪽 자식 노드를 방문한다.
        preorder(node.right); // 오른쪽 자식 노드를 방문한다.
    }
}

이 함수는 이진 트리의 루트 노드를 매개변수로 받아, 나무를 타는 방법preorder으로 이진 트리를 탐색한다. 매개변수로 전달된 노드가 NULL이 아니면, 현재 노드를 방문하고 왼쪽 자지 노드와 오른쪽 자식 노드를 각각 preorder 함수를 재귀적으로 호출한다. 이 함수는 재귀적인 방법으로 이진 트리를 순회하므로, 호출 스택의 깊이가 증가함에 따라 성능이 저하될 수 있다.

재귀적 풀이 (recursive) 예

분할 통치

class Solution {
    public int solution(int balls, int share) {
        int answer = 0;
        if(balls == share || share == 0) 
            answer = 1; 
        else{
            answer = solution(balls - 1, share - 1) + solution(balls - 1, share);
        } 

        return answer;
    }
}

• 입력 : 두 정수 balls와 share
• 출력 : balls개의 공을 share 명의 사람에게 나누어주는 방법의 수

$nCr = n-1Cr + n-1Cr-1$

예를들어, 3개의 구슬 (1,2,3) 중 2개를 뽑는다고 가정하면3C2 = 2C2 + 2C1이다.

• 1, 2, 3 중 1을 선택하지 않는 경우 2,3을 모두 선택해야 하므로 -> 2C2
• 1, 2, 3 중 1을 선택하는 경우 2,3 중 1개를 선택해야 하므로 -> 2C1

• 이 함수는 다음과 같은 점화식을 사용하여 문제를 해결합니다.

1. 기저 조건(base case) : 만약 balls와 share가 같거나 share가 0이면, 리턴은 1입니다. 이것은 모든 공을 동일한 수로 나눌 수 있거나 공을 나눌 필요가 없는 경우를 의미
2. 재귀적 접근(recursive approach) : 그렇지 않으면, 함수는 다음 두 가지 경우의 합을 반환

• balls - 1 개의 공을 share - 1명의 사람들에게 나누어주는 방법의 수 : 이 경우는 각 사람들이 최소한 하나의 공을 가지고 있는 경우를 의미함
• balls - 1 개의 공을 share 명의 사람들에게 나누어주는 방법의 수 : 이 경우 적어도 한 사람이 공을 받지 않는 경우를 의미함