1. Now this will run on my 486?
This was a type of problem that required analyzing the operation of a binary to obtain the required input value.
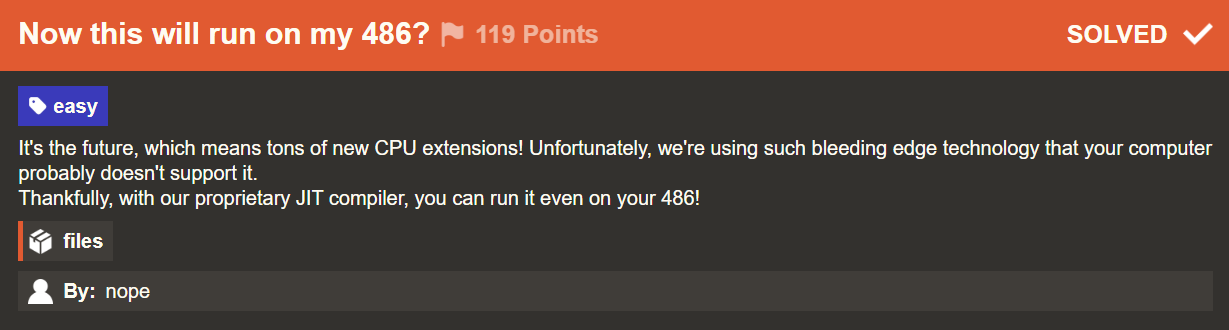
A unique feature of this binary is that instead of performing instruction unpacking before executing the code, it registers a handler function for the illegal instruction signal and unpacks one code gadget at a time. This made the process of analyzing the code a bit more complicated.
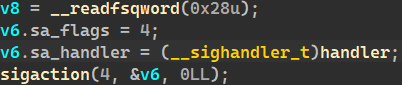
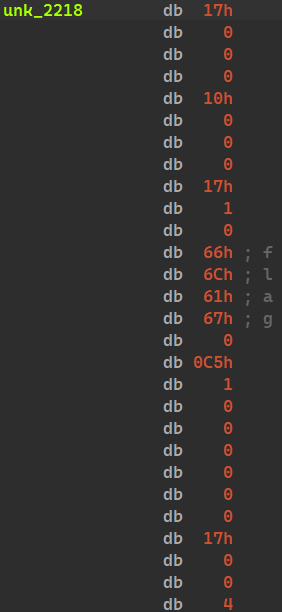
The code in this area is executed one by one to issue an illegal instruction.
However, I was able to make the code readable by using IDA's dynamic analysis capabilities and the ability to customize signal processing options. Since the operation itself was a simple xor, I was able to solve the problem without writing any separate exploit code.
2. Crispy Kelp
Here is a binary written in Golang.
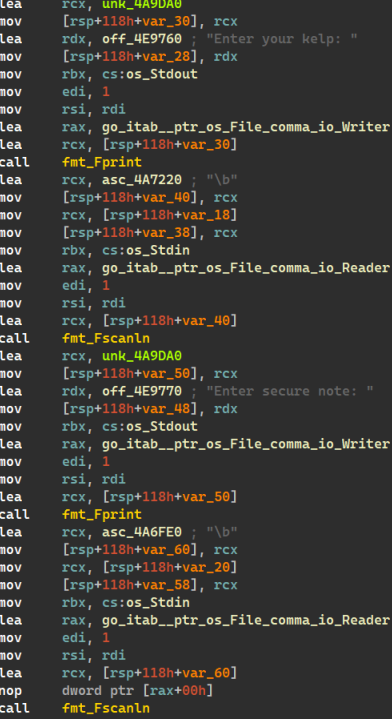
When this binary first starts, it asks for a kelp (integer) value and a secure note (4-byte Unicode string). It receives these two values and passes them to encodeString to perform encoding.

In this function, a 4-byte string as long as the secure note is randomly generated, and a string of (length of secure note) * 2 + 1 is generated according to the following rules.
First, a string as long as the secure note is generated according to the following rules.
encoded[i]=(secure_note[i]^rand[i])+kelp
After that, the kelp value is attached, and a string as long as the secure note is generated again according to the following rules.
encoded[i+note_len+1]=(rand[i]^encoded[i])+kelp
By utilizing this, the rand value can be found out with the attached encoded string, and the secure_note can be found out with this rand value.
res=b'\xeb\xb3\x98\xeb\xb5\x8c\xeb\xb5\x94\xeb\xb3\x89\xeb\xb3\xa4\xeb\xb4\xb1\xeb\xb6\x93\xeb\xb2\xb4\xeb\xb5\x8f\xeb\xb3\x8d\xeb\xb5\xa3\xeb\xb5\x9c\xeb\xb3\xa2\xeb\xb6\x82\xeb\xb6\x8e\xeb\xb3\x9d\xeb\xb4\x85\xeb\xb3\xb3\xeb\xb4\x88\xeb\xb4\x80\xeb\xb2\xac\xeb\xb5\x80\xeb\xb3\x9f\xeb\xb5\x8d\xeb\xb5\x9c\xeb\xb5\xb5\xeb\xb4\xab\xeb\xb3\xa4\xeb\xb6\xa2\xeb\xb5\xbf\xeb\xb6\x9a\xeb\xb4\x8c\xeb\xb5\xb2\xeb\xb4\x86\xeb\xb3\xb7\xeb\xb5\xb6\xeb\xb4\xb1\xeb\xb5\x8f\xeb\xb6\xa4\xeb\xb5\x87\xeb\xb4\x8a\xeb\xb5\x83\xeb\xb3\x82\xeb\xb5\x9a\xeb\xb3\x85\xeb\xb3\x95\xeb\xb3\x84\xeb\xb2\xac\xeb\xb2\xa6\xf0\x97\xa4\xa9\xf0\x97\xa8\xbe\xf0\x97\xa8\xb9\xf0\x97\xa4\xbf\xf0\x97\xa5\x9f\xf0\x97\xa9\xb4\xf0\x97\xa6\xbe\xf0\x97\xa5\xa7\xf0\x97\xa8\xb3\xf0\x97\xa5\xbf\xf0\x97\xa9\x98\xf0\x97\xa9\x80\xf0\x97\xa4\xa7\xf0\x97\xa8\x95\xf0\x97\xa6\xbb\xf0\x97\xa5\x9b\xf0\x97\xa8\x94\xf0\x97\xa6\x87\xf0\x97\xa6\xa8\xf0\x97\xa8\x8f\xf0\x97\xa5\x84\xf0\x97\xa9\x9c\xf0\x97\xa4\xb8\xf0\x97\xa8\xa8\xf0\x97\xa8\xb9\xf0\x97\xaa\x8b\xf0\x97\xaa\x82\xf0\x97\xa6\x8f\xf0\x97\xa7\x94\xf0\x97\xa9\xb0\xf0\x97\xa8\x80\xf0\x97\xa6\xaf\xf0\x97\xa8\xb3\xf0\x97\xa6\xb1\xf0\x97\xa4\xbb\xf0\x97\xa9\xae\xf0\x97\xa8\xb3\xf0\x97\xa9\x9f\xf0\x97\xa7\xa2\xf0\x97\xa9\xbc\xf0\x97\xa7\x82\xf0\x97\xa8\xa7\xf0\x97\xa5\xa3\xf0\x97\xa8\xac\xf0\x97\xa6\x91\xf0\x97\xa4\xb0\xf0\x97\xa6\x95\xf0\x97\xa5\xbd'.decode('utf-8')
res_rune=[(ord(c)) for c in res]
print(res_rune)
input_len=len(res_rune)//2
secret_note=res_rune[input_len]
print('secret note : ', secret_note)
for i in range(input_len):
cur_rand=(res_rune[i+input_len+1]-secret_note)^res_rune[i]
print(chr((res_rune[i]-secret_note)^cur_rand), end='')3. Bunny Jumper!

When you access the problem site, you will see a flag checker like this.
First, I looked for the code to figure out the logic of the flag checker and found that the logic was about 1800 lines long due to jump table obfuscation. Since it was not a code that could be read in the order it was shown, I wrote a Python script that generated code that outputs the process that was being executed.

total_code=open('code.js', 'r').read().split('\n')
new_code=""
for i in range(len(total_code)):
token=total_code[i].lstrip(' ').split(' ')[0]
tmp_token=""
if len(total_code[i].lstrip(' ').split(' '))>1:
tmp_token=total_code[i].lstrip(' ').split(' ')[1]
if token!="for" and token!="if" and token!="continue" and token!="break" and token!="}" and token!="function" and token!="var" and token[-1]!=':' and ((token!='C' or tmp_token!='=')):
new_code+="console.log(\'"+total_code[i].lstrip(' ')+"\')\n"
new_code+=total_code[i]+"\n"
open("new_code.js", "w").write(new_code)When you run the above code, it will print all the code except the code that goes to another jump table to console.log. And when you run it,
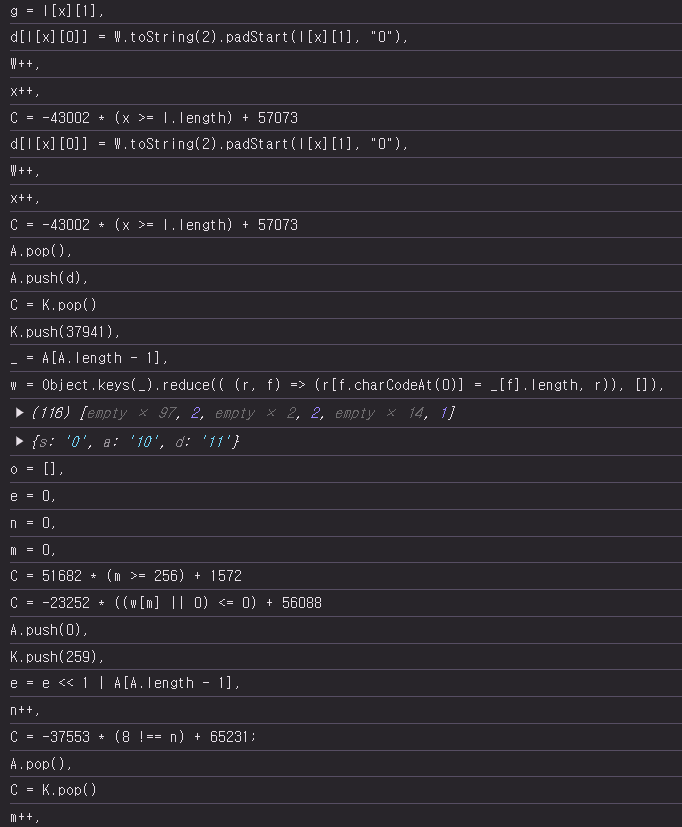
it will print the execution process at a glance like this.
To summarize, pick 4 characters from all flags, and create a tree based on the number of times each character appears in the multiset of picked characters.
After that, a number is assigned based on the relative height of each character in the tree, and jumpjump...jumpit is split into bits and encoded according to the following rule.
Starting from the ASCII code index of each character assigned the number generated above, the number assigned to that character and the above string are XORed.
The exploit code is as follows.
from base64 import b64decode
table=[ord(i) for i in 'jumpjumpjumpjumpjumpjumpjumpjumpj']
base_table=["dW1wQtXNWGp", "dW1xKnVFcS9", "dW1xKnVFWH5", "dW1xLHXNcGp", "dW1wCnVFcG9", "dW1x6PVtWGp", "dW1xL3VucGp", "dW1xKn9ucGp", "dW1xKtVtdmp", "dW1xKiVtdmp", "dW1xKPZtcGp", "dW1wanfucH5", "dW1x6nVFcH5", "dW1wfnVtEG9", "dW1xL3ZtcGp", "dW1waXVv+mp", "dW1wCnVt1Wp", "dW1x6zVv8Gp", "dW1wQnBtaGp", "dW1wOnVsMAp", "dW1xKhU9cGp", "dW1xKnVucSp", "dW1wcn89cGp", "dW1x6nVtcGp", "dW1wanVtEGp", "dW1wahVtcGp", "dW1wanZtcGp", "dW1wanVrcGp"]
idx_table=[170208564, 303307048, 320086583, 387656501, 286799160, 236723758, 185603370, 168895531, 153103667, 152903206, 135141663, 119284279, 118959923, 253767992, 102047534, 84281399, 85665324, 68360487, 51782960, 51128620, 35464242, 18095146, 268849, 219753011, 202515241, 143414, 168894767, 151986214]
poss=[[] for i in range(58)]
used_table=[]
ref_table=[]
for bl in range(len(idx_table)):
cur=[i for i in b64decode('anVtcGp1bXBq'+base_table[bl]+'1bXBqdW1wanVtcGp1bXBq')]
diff_arr=[]
for i in range(8*len(cur)):
bidx, sidx=i>>3, i&7
f, s=(table[bidx]>>(7-sidx))&1, (cur[bidx]>>(7-sidx))&1
if f!=s:
diff_arr.append(i)
sum=0
used=[]
for i in range(0, len(diff_arr), 2):
if diff_arr[i+1]-diff_arr[i]==1:
used.append([diff_arr[i]-sum, 1])
elif diff_arr[i+1]-diff_arr[i]==2:
used.append([diff_arr[i]-sum, 2])
sum+=4
cidx=len(used_table)
used_table.append(used)
ref_table.append(0)
vst=[0]*58
for i in range(4):
ii=idx_table[bl]&255
idx_table[bl]>>=8
if ii>=58 or vst[ii]:
continue
poss[ii].append(cidx)
ref_table[len(ref_table)-1]+=1
vst[ii]=1
for i in range(len(used_table)):
cur=used_table[i]
cur.sort(key=lambda each: each[1])
new_cur=[]
if len(cur)==1:
new_cur=[cur[0][0]]*ref_table[i]
elif len(cur)==3:
if ref_table[i]==4:
new_cur=[cur[0][0], cur[0][0], cur[1][0], cur[2][0]]
else:
new_cur=[cur[0][0], cur[1][0], cur[2][0]]
else:
new_cur=[cur[0][0], cur[1][0], cur[2][0], cur[3][0]]
used_table[i]=new_cur
target_cnt=57
flag_arr=[0]*58
idx=0
while target_cnt:
max_cnt, max_idx=0, -1
ccnt=[0]*256
for i in poss[idx]:
vst=[0]*256
for j in used_table[i]:
if vst[j]==0:
ccnt[j]+=1
if ccnt[j]==len(poss[idx]):
max_cnt+=1
max_idx=j
vst[j]=1
if max_cnt==1:
flag_arr[idx]=max_idx
for i in poss[idx]:
used_table[i].remove(max_idx)
target_cnt-=1
idx=(idx+1)%58
for i in flag_arr:
print(chr(i), end='')
no jam