Entropy

엔트로피는 불확실성의 정도이다. 즉, 확률과 연관된 개념으로써
엔트로피가 높다는 것은 미래의 사건이 뭐가 나올지 불확실한정도가 크다는 것이고 낮다는 것은 미래의 사건이 뭐가 나올지 비교적 확실하다는 것이다.

엔트로피는 확률분포와 연관해서 기억하면 좋을 것이다.

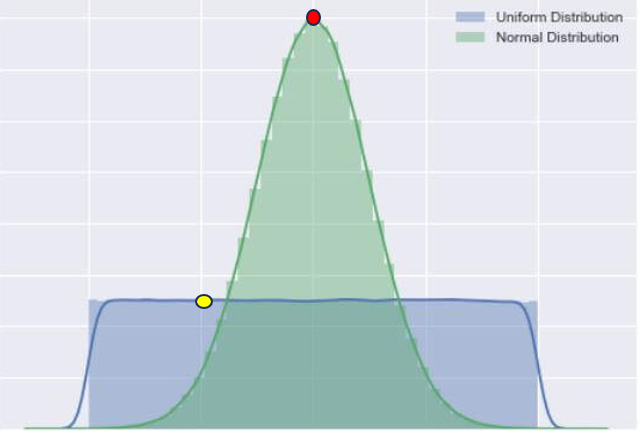
위의 두 확률분포에 대해서 우리는 빨간색 점의 사건이 일어날 확률은 비교적 높은 것을 알 수 있다. 그렇다면 우리가 당신에게 정규분포에 해당하는 사건들 중에서 어떤 사건이 일어나는데 5만원을 걸래? 라고 한다면 당신은 빨간색점의 사건이 일어나는데 돈을 걸겠다고 할 것이다.

왜냐? 좀 더 일어날 확률이 높으니까 자 그렇다면 반대로 노란색 점의 사건이 있는 확률분포를 확인해보자. 우리는 당신에게 똑같이 파란색 분포(Uniform Distribution)에 해당하는 사건들중에 어떤 사건이 일어나는데 5만원을 걸래? 라고 한다면 당신은 선뜻 노란색 사건이 일어나는데 돈을 걸겠다고 하지 않을 것이다. 왜냐하면 "불확실한 정도"가 높으니까.

이러한 방식으로 엔트로피를 이해하면 좋다 따라서 엔트로피가 높다는 것은 불확실한 정도가 높다는 것이고 이는 곧 Uniform Distribution에 가까운 확률분포라는 것이다.

반대로 엔트로피가 낮다는 것은 불확실한 정도가 낮다는 것이다.

위의 예시에서는 불확실한 정도에 대한 관점에서 엔트로피를 설명했다. 그렇다면 정보이론의 관점에서 엔트로피를 생각해보자.

자, 만약에 내가 당신에게 문자를 보내는데 100자중에서 절반이 하트라고 해보자. 문자를 Bit로 표현한다고 하면 하트를 어떻게 표현해야지 가장 메모리를 적게 사용할까?
→ 바로 0이다.
자 그렇다면 이제 확률이 높으면 높을수록 표현하는 Bit의 갯수를 줄이면 메모리를 적게 사용할 것 같다는 느낌이 든다. 이를 표현한 것이 바로 아래의 엔트로피 식이고, 그렇다면 엔트로피는 또 다르게 표현할 수 있을 것이다.

정보를 다양하게 표현할 수 있는데 그중에 Lower Bound(하한)의 정보의 양

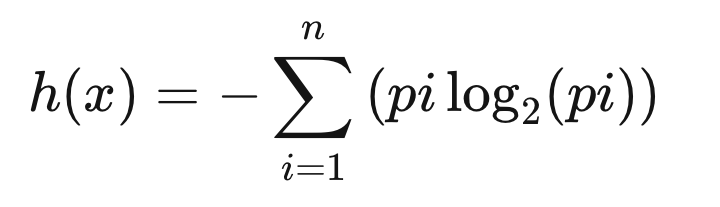
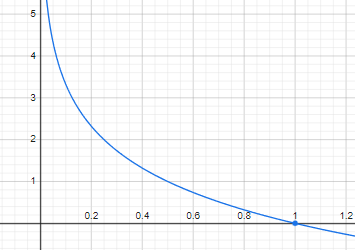
$-log_2(x)$의 그래프로써 y축을 정보의 양이라고 생각한다면 확률이 높아지면 높아질수록(덜 불확실할수록) 더 적은 정보의 양으로 표현한다고 생각하자.

CrossEntropy

크로스 엔트로피는 한마디로 말하자면 다음과 같다.
"틀릴 수 있는 정보를 가지고 추정한 엔트로피"

우리가 만약에 어떤 사건들이 일어날 확률분포를 예측했다고 하자. 이 분포를 이용해서 구한 엔트로피를 크로스 엔트로피라고 한다.
"즉 내가 예측한 분포로 정보를 표현했을때 실제로 표현되는 정보의 양" 으로 이해하면 좋을 것 같다.

CrossEntropy를 이해하는데 불확실성의 개념을 연결하는데는 쉽지 않은 것같다.

크로스엔트로피를 구하는 식은 다음과 같다.
$log$안에 들어있는 것$(p(x))$ 가 내가 예측한 분포이다.

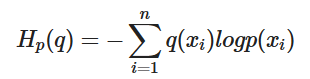
KL-Divergence

KL-Divergence는 Entropy를 이용해서 두 분포 사이의 차이를 측정하는데 쓰이는 측정지표이다 단순하게 CrossEntropy에서 실제 Entropy를 빼는 것으로 두 분포사이의 차이를 측정한다.

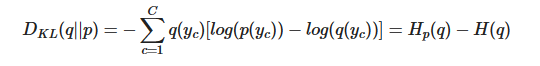
우리는 Loss Function으로 Cross Entropy를 이용해서 모델을 학습시키곤 하는데, 그 이유는 위에서 말했듯이 Entropy가 최소이므로 Cross Entropy를 최소로 만드는 것은 정답 확률분포에 다가가도록 만드는 것과 같은 것이다.

참고>유튜브