안녕하세요, 현재 인천대학교에서 AIDML연구실에서 Undergraduate Researcher로 있는 이성준 이라고 합니다. TimeSeries에 대한 ForeCasting 및 Analysis가 관심사이고 추후에는 Anormaly Detection 또한 연구해볼 생각이 있습니다.
오늘은 저의 첫번째 발표 주제였던 Classical Forecasting에 대해서 글을 포스팅 하겠습니다.
(구글링을 통해서 공부했고 베이스가 된 책은 다음과 같습니다.
링크텍스트)
딥러닝에 기반한 ForeCasting기법이 최근에 나오곤 있지만, 아직까진 Classic한 ARIMA,SARIMA
와 같은 ForeCasting기법이 대세를 이루고 있는 만큼 Classical ForeCasting을 다루기 전에 꼭 알아야 하는 기반지식을 기술하겠습니다.
연구발표간에 검토해 잘못된 지식은 없을 것이라고 생각하지만 혹시나 있다면 지적해주시면 감사하겠습니다
오늘 다룰 KeyWord는 다음과 같습니다
Stationary
AutoCorrelation
WhiteNoise
Classical Decomposition(SMA)
Classical ForeCasting
개요는 다음과 같습니다
가. What can we forecast
1. 예측가능한 것은 무엇이고 예측하기 쉽게 만드는 요소는 무엇이 있는가
2. 예측에 대한 통계적인 약속(예측구간, 예측분포 등)
나. What is Time Series?
1. Time series란 무엇인가, Time Series의 특징
2. 상관계수와 자기상관계수 그리고 ACF``
3. Time Series의 백색잡음과 백색잡음의 기준
다. Deal with Data of Time Series
1. 수학적인 변환 (Box-Cox 변환)
2. 분해를 통한 시계열 데이터 분석
라. Forecasting Time Series Data
1. 시계열 분석의 workflow
2. 몇가지 단순한 예측기법
3. 분해를 통한 예측
(예측이 잘 됐는가를 잔차로 판단)
4. 잔차(Residual)는 무엇인가
5. 잔차가 white noise임을 판단하는 방법
- 5-1. 귀무가설과 대립가설
- 5-2. 카이제곱분포와 검정
- 5-3. 잔차에 대한 박스 피어스 검정과 융박스 검정
6.예측분포와 예측구간
- 6-1. 예측기법 별로 h 단계 예측분포와 그 표준편차
- 6-2. 한단계 예측구간과 여러 단계 예측구간
- 6-3. box-cox의 역변환
- 6-4. 역변환으로 생긴 중간값의 편향 조정하기
- 6-5. 예측정확도 평가하기
마.Linear model with time series
1. 단순선형회귀와 다중선형회귀
2. 예측변수로 설정하면 유용한것들
3. 회귀 모델 비교
4. 예측의 종류
5. 상관관계와 인과관계
6. 다중공선성(colinearlity)
What can we forecast
1. 예측가능한 것은 무엇이고 예측을 쉽게 만드는 요소는 무엇이 있는가
우리는 직관적으로 내일 발표될 로또 당첨번호와 내일의 날씨 둘중에 어느것이 예측하기 쉬운가 라고 물어본다면 당연하게도 날씨가 예측하기 쉽다고 할 것이다.
그렇다면 어떠한 차이가 예측가능성을 좌우 하게 될까?
첫번째로, 예측에 영향을 주는 요인을 얼마나 이해하고 있냐가 될 수 있고
두번째로, 사용할 수 있는 데이터가 얼마나 많은지가 될 수 있고
세번째로, 우리가 예측함으로써 예측에 영향을 줄 수 있는지 여부가 있다.
마지막이 약간 이해가 힘들 수 있는데 예를 들어, 주식시장에서 우리가 주가를 예측해서 칼럼을 작성한다고 하자. 그럼 우리가 예측하는 주가가 우리의 칼럼에 의해 영향을 받을 수 있다.
예측은 과거 데이터를 바탕으로 패턴을 잡아내서 예측하는 것이다. 따라서 우리는 예측할때 과거의 환경이 변하는 방식이 미래에도 계속 될 것이라는 가정을 깔아둔다.
다시 말해 불안정한 환경은 계속 불안정할 것이고 판매량이 변하는 사업은 계속 판매량이 변할 것이고 호황과 불황의 패턴을 보이는 경제는 계속해서 호황과 불황이 나타날 것이라는 것이다.
2. 예측에 대한 통계적인 약속(예측구간, 예측분포 등)
우리가 예측하려는 대상이 알려져 있지 않다면 이 대상을 우리는 확률변수(Random variable)로 생각할 수 있다. 우리는 이 확률변수가 가질 수 있는 값을 구간으로 가질 수 있다.
예를 들어 80%예측구간은 이 구간안에 확률변수가 들어있을 확률이 80퍼센트라는 뜻이다.
우리는 이 예측구간의 평균을 점예측(point forecast)라고 하기로 하자.
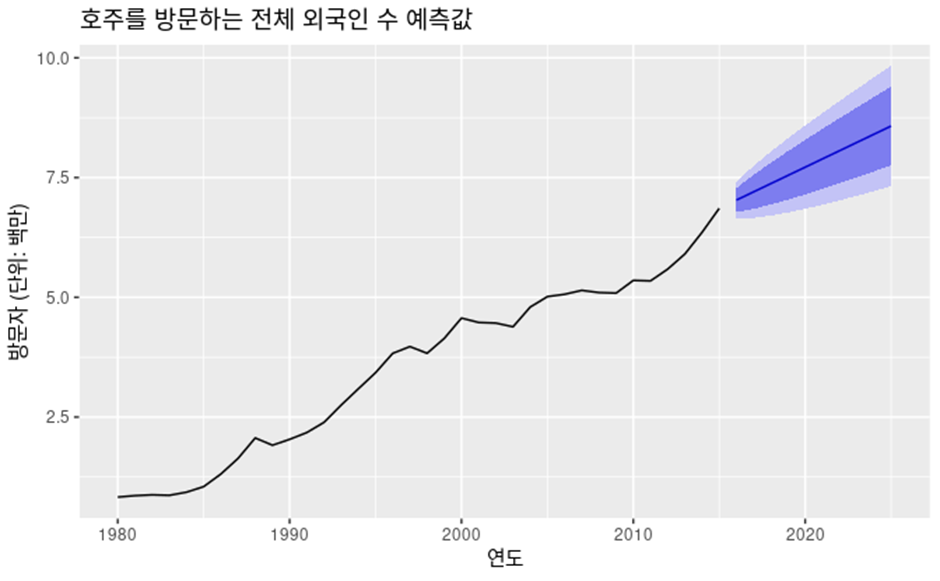
기호적인 약속
y_t는 시간 t 에서의 관측값을 나타낸다.
y_t|I에서 I는 우리가 이미 알고 있는 관측값의 집합이고 y_t 는 우리가 예측하고 싶은 것 이다. 즉, I 가 주어졌을 때 우리가 예측할 값 y_t를 의미한다. 상대적인 확률 값에 따라 이 y_t가 가질수 있는 값을 y_t|I 의 확률분포 라고 하고 예측할 때는 예측 분포(forecast distribution)이라고 한다.
우리가 보통 예측을 말할 때는 예측분포의 평균을 가르키고 y ̂_t 으로 쓴다.
비슷하게 y ̂_T+h|T은 y1,…,yT 을 고려하는 y_T+h의 예측을 의미한다.(즉, 시간 T까지의 모든 관측값을 고려한 h단계 예측을 말한다)
What is Time Series?
1. Time series란 무엇인가, Time Series의 특징
Time Series(시계열)은 시간에 흐름에 따라 생기는 데이터를 의미한다 시계열 데이터는 다음과 같은 특징을 가질 수도 있다
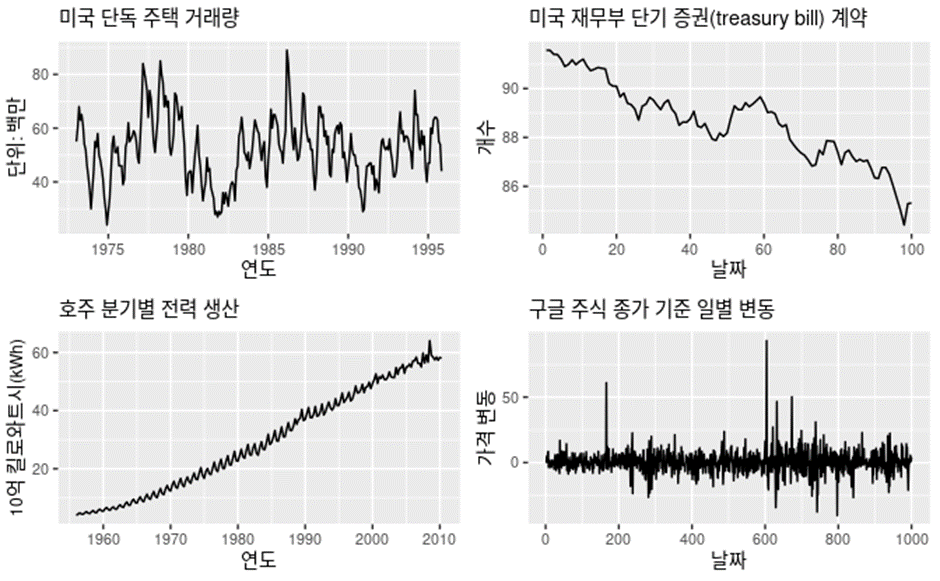
a) Trend(추세)
데이터의 증가추세 감소추세를 생각하면 된다.
위 그래프 중 미국 재무부 단기 증권 계약 그래프를 보면 감소추세의 그래프를 볼 수 있다
b) Seasonality(계절성)
어떤 시기에 관련된 성질이다 예를 들어서 해마다 특정달에 나타난다 거나 주마다 특정요일에 나타난다 거나 계절성요인이 시계열에 영향을 줄 때 계절성 패턴이 나타난다.
호주 분기별 전력생산을 보면 강한 계절성과 함께 강한 증가추세를 보인다
c) 주기(Cyclic)
계절성이 고정된 주기로 생기는 패턴을 의미한다면 주기는 이와 달리 고정된 주기가 아닌 주기로 패턴이 생기는 것을 의미한다
미국 단독 주택 거래량을 보면 5년마다 계절성이 생김과 동시에 6-10년마다 주기적인 패턴이 생기는 것을 볼 수 있다
2. 상관계수와 자기상관 계수 그리고 ACF
우리는 종종 두 시계열 데이터가 서로에 대해 얼마나 의존하는지 살펴볼 필요가 있다.
상관계수(correlation coefficient)가 두 시계열 데이터의 의존성을 정량화 한 통계량이다.
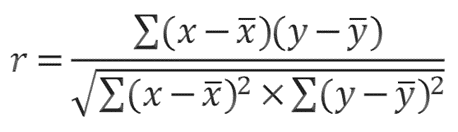
다음과 같이 쓸 수 있는데 분자가 의미하는게 바로 공분산(Covariance)이다 공분산은
E((X-Xbar)(Y-Ybar))로 쓸 수 있는데 이 공분산이 의미하는게 X와 Y의 의존성을 보여주기 위함이다 즉 X가 X의 평균보다 클 때 Y도 Y의 평균보다 크면 둘의 평균은 양수가 될 것 이고 X가 큰값을 가지면 Y도 큰값을 가진다는 의존성을 보여주고 반대도 마찬가지다 하지만 공분산은 X와 Y가 양의 상관관계인지 음의 상관관계인지만 알려주고 어느정도 의존하는지는 알려주지 않기 때문에 이를 표준편차로 나눠서 -1과 1 사이로 정량화 한게 바로 상관관계이다.
따라서 r>0 이면 두시계열 데이터가 양의 상관관계를 갖음을 알 수 있고 r<0 이면 두시계열 데이터가 음의 상관관계를 갖음을 알 수 있고 r=0이면 상관관계가 없음을 알 수 있다
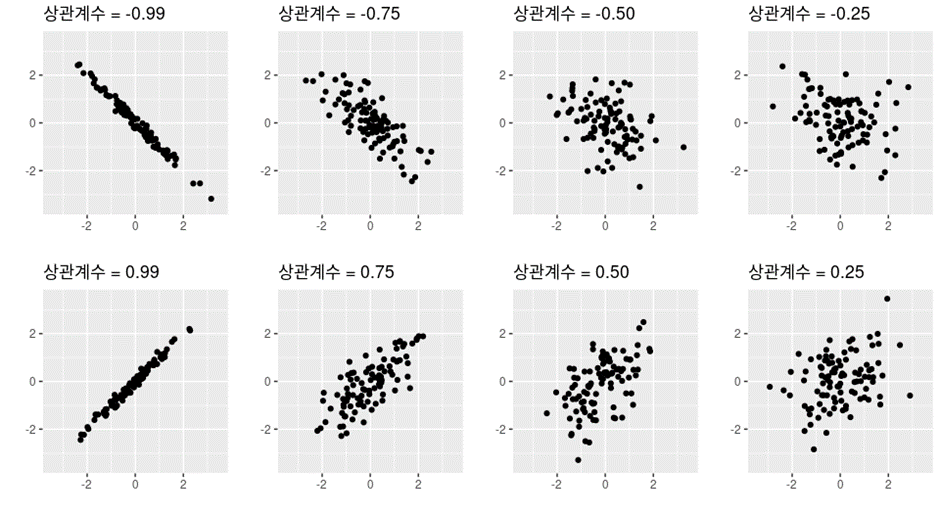
시계열 분석에는 자기상관계수(autocorrelation)이 존재한다
-> 시계열의 시차값(lagged values)(현재 시계열과 그 시계열과 x차 시점)사이의 선형관계를 측정한다. 여기서 명심할 점은 자기상관계수는 다른 시계열과 비교 하는게 아닌 하나의 시계열만 사용한다는 점이다. 따라서 plot을 그릴때 Y축은 상관관계이고 X축은 지연 시간 단위의 수이다
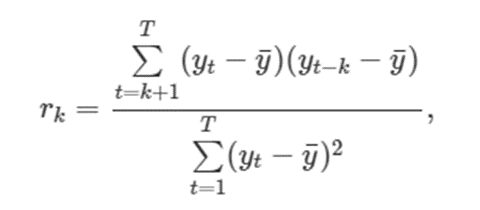
우리는 아주 일반적인 ACF(Auto Correlation Function)를 보자
- 계절성과 추세를 가진 데이터에 대한 ACF
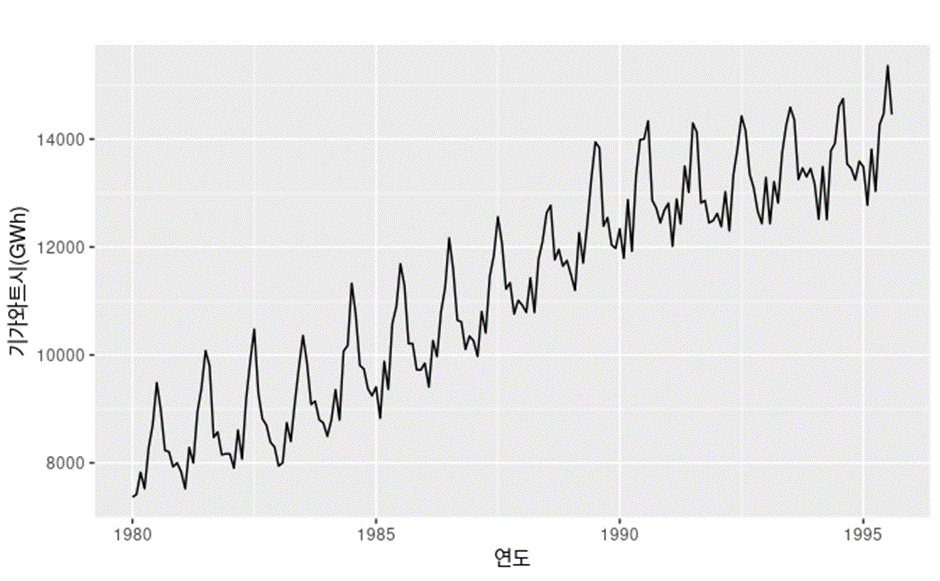
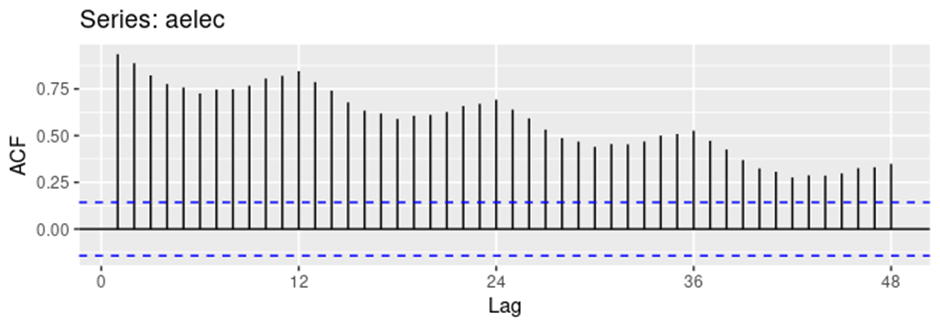
위 데이터를 보면 계절성이 나타남과 동시에 값이 추세를 따라 커지기 떄문에 기준으로 삼은 값과의 차이가 커지면서 상관관계가 감소함을 볼 수 있다
부분자기상관계수
부분자기상관계수를 간단하게 설명하기 위해서는 X를 연간 신발 판매량 Y를 연간 범죄발생 건수라고 해보자
이 둘의 상관계수를 계산해보면 상당히 높은 값이 나온다 이유는 시간이 지나면서 인구수가 늘어났고 따라서 신발 판매량이 커질 때 범죄발생 건수도 커진 것 이다 따라서 둘의 순수한 상관관계를 보기위해서 시간의 효과를 제거한 상관관계가 부분자기상관계수이다 두 시차 사이의 순수한 상관계수라고 할 수 있다 자기상관계수는 y_t-1과 y_t 사이의 상관계수가 있고 y_t와 y_t+1사이의 상관계수가 있을 때 y_t-1과 y_t+1이 실제로는 상관계수가 없는데 상관계수가 있다고 나올 수 있는데 이것을 제거한 것이 바로 부분자기상관계수이다
(Partial Auto Correlation 계산하는 방법은 추후 포스팅에서 다룰 예정이다)
3.Time Series의 백색잡음과 백색잡음의 기준
Noise는 피할 수 없는 외부요소로 발생하는 잡음이다. 통제할 수 없는 요소에 의해 발생하는 것인데 시계열 데이터 분석시에 noise를 처리하는 작업을 해야하는데 여기에 필요한 개념이 white noise이다 처리라는 개념보단 어쩔 수 없는 오차로 본다는 것이다
백색잡음(White noise)가 되기 위해서는 오차사이의 상관관계가 없고 이 오차는 정규 분포(평균이 0 이고 분산이 Sigma^2)인 분포를 따른다고 기대한다 하지만 어떤 무작위성 변동 때문에 정확히 0은 아닐텐데 따라서 white noise가 정규분포 N(0,1/T)를 따른다고 가정하고 noise의 ACF에서 뾰족한 막대의 95퍼센트가 $±1.96/√⊤ $ 안에 들어오면 백색잡음 이라고 한다
Deal with Data of Time Series
1.수학적인 변환
우리는 수학적인 변환을 통해서 데이터 사이의 큰 차이가 나는 경우 조정할 수 있다
이를 다시 말하자면 데이터분포의 모양(Skew)을 조정해준다
a) 거듭곱 변환 (Power transformation)
w_t = (y_t)^p 로 쓰고 p에 알맞은 값을 넣어서 제곱근 혹은 세제곱근등을 사용 할 수 있다
EX> 사진출처 https://seeyapangpang.tistory.com/35
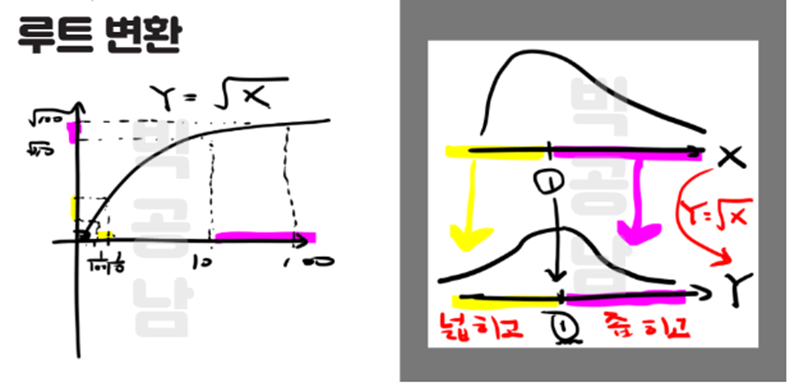
1보다 작은값 들에 대해서는 크기를 키워서 넓히고 1도다 큰 값들에 대해서는 크기를 작게 해서 좌우 대칭을 맞춘다
b) 로그 변환 (log transformation)
w_t = log(y_t)로 쓴다 로그 값으로 바꾸면서 로그값이 1이 증가할때마다 원래값은 10이 증가한셈이 된다.
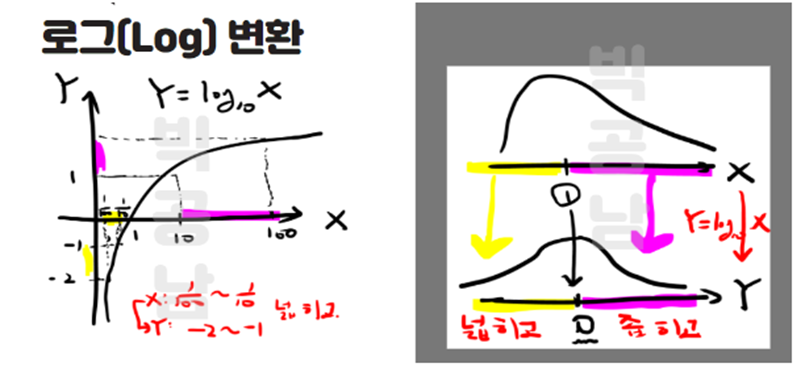
c) 박스-칵스 변환(Box-Cox transformation)
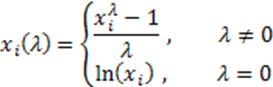
Box-Cox 변환도 위의 변환처럼 데이터들이 정규분포를 따를 수 있게 거치는 변환과정이다 박스-칵스 변환에서는 데이터의 분포가 정규분포가 될 수 있게 하는 lambda 값을 찾는 것이 포인트이다
2.분해를 통한 시계열 데이터 분석
시계열 데이터는 다양한 패턴으로 나타난다 이런 시계열을 몇가지 성분으로 나누는 작업은 시계열을 이해하는데 도움이 된다 시계열을 추세 주기 계정성으로 나눌 때 종종 추세와 주기를 결합해 추세-주기 성분으로 다룬다. 따라서 다음 3가지 성분으로 구성된다
1) 추세-주기 성분, T_t
2) 계절성 성분, S_t
3) 나머지 성분, R_t
고전적인 분해
이동평균을 이용하여 직접 계산도 가능하다
Additive Decomposition)
Multiplication Decomposition)
계절성 요동의 크기나 추세-주기의 변동폭이 시간에 의해 변하지 않으면 덧셈 분해가 적절하다
계절성 요동의 크기나 추세-주기의 변동이 시간에 따라 비례하면 곱셈분해를 사용한다
일단 곱셈 분해를 사용하고 시계열의 변동이 시간에 따라 안정적으로 나타나면 데이터를 변환해서 덧셈분해를 사용하는것도 한가지 방법이다
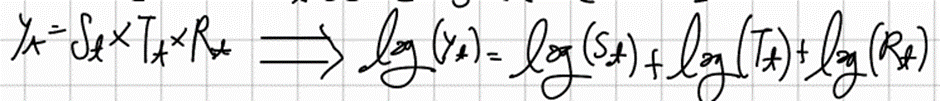
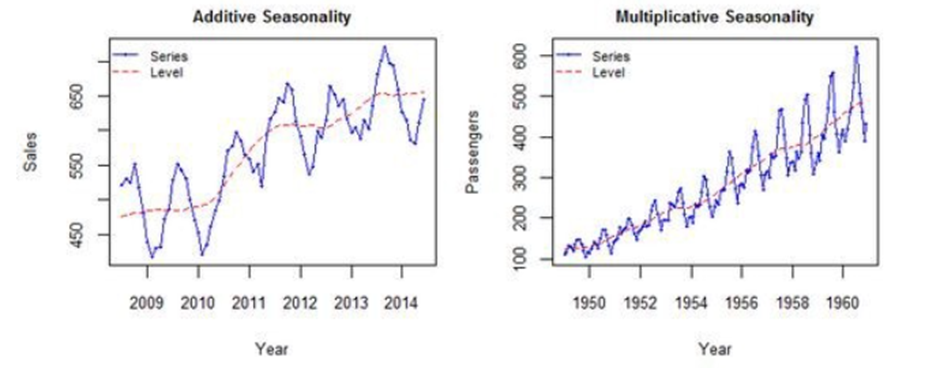
왼쪽은 Additive Decomposition이 적절하고 오른쪽은 multiplicative가 적절하다
Seasonally Adjusted Data
원본데이터에서 계졀성분을 제거한 결과값을 “계절성으로 조절된 데이터” 라고 한다. 덧셈분해에서 계절성으로 조절된 데이터는 y_t-S_t로 주어지고 곱셈분해에서는 y_t/S_t로 주어진다
이러한 조정은 계절성에의한 변동이 주된 관심사가 아니라면 유용하다.
예를 들면 월별 실업률 데이터는 계절성 변동(학교를 졸업한 사람들의 구직) 등 과 같은 변화보다는 중요한 경제상황 때문에 나타나는 변동을 강조하기 위해 데이터를 계절성으로 조정한다.
이동평균
고전적인 분해방법의 첫 번째 단계는 추세-주기를 측정하기 위해 이동평균(moving average)방법을 사용하는 것이다.
이동평균 평활( 변동의 폭이 큰 시계열 데이터를 변동이 완만하게 바꾸는 것 )
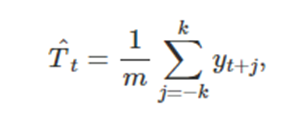
여기서 m=2k+1이다, 즉 m기간 안의 시계열의 값을 평균하는게 시간 t에서의 추세-주기를 측정하는 방법이다 이것을 차수 m의 이동 평균이라는 의미에서 m-MA(Moving Average)라고 한다
EX>
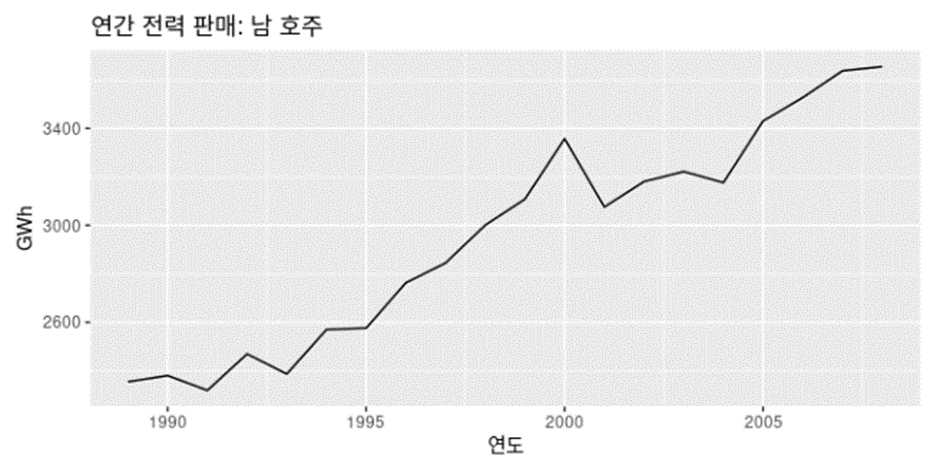
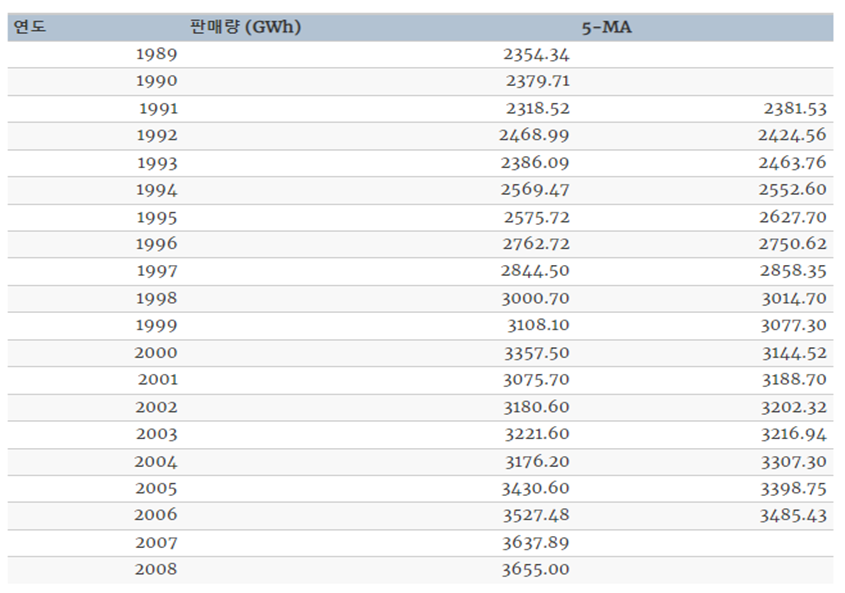
만약 짝수 차수의 이동평균을 하려면 이동평균의 이동평균을 해주어야 한다 이는 대칭적으로 더하기 위한 작업이다
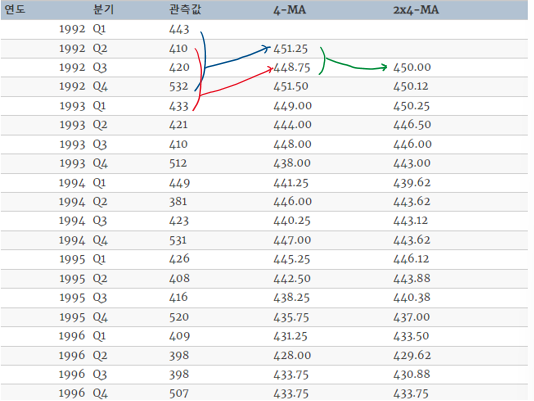
최종적으로 관측값은 대칭적으로 더한셈이 된다
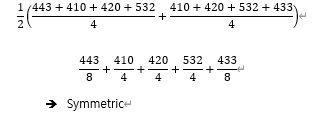
Additive Decomposition의 방법
1단계: 이동평균법으로 추세주기성분을 계산한다
2단계: 추세주기성분을 제거한 시계열을 계산한다
3단계: Season마다 Seasonal성분을 측정하기위해 2단계에서 구한값의 평균을 구한다.
예를 들어 3월의 계절성분은 데이터에서 추세를 제거한 데이터의 모든 3월 값의 평균이다.
4단계
R_t = y_t - T_t - S_t로 구한다
Multiplicity Decomposition의 방법
1단게: 이동평균법으로 추세-주기성분을 계산한다
2단계: y_t/T_t로 추세를 제거한 시계열을 계산한다
3단계: 위의 방식과 같이 계절성을 구한다
4단계: R_t = y_t/(T_t x S_t)로 나머지 성분을 구한다
고전적인 분해에 대한 몇가지 문제점
1. 이동평균법을 사용하기 때문에 처음 몇 개의 관측값과 마지막 몇 개에 대한 추세 추정값을 얻을 수 없다
2. 추세-주기 측정은 이동 평균법에 의해 데이터에 나타나는 급격한 증가나 감소를 과도하게 매끄럽게 한다
3. 계절성분이 매 년 반복된다는 것을 가정한다. 더욱 긴 시계열에 대해서는 이러한 계절적인 성분이 통하지 않을 수 있다.
EX> 전기 수요 패턴은 에어컨의 보급으로 시간에 따라 변했다. 최대 수요가 에어컨의 보급으로 난방에 의한 겨울보다 여름으로 바뀌었다
이러한 문제점을 개선한 X11 분해, STL분해, SEAT분해등이 나왔다
Forecasting Time Series Data
1. 시계열 분석의 workflow
예측의 일처리 순서는 다음과 같다
a) Preparing Data
b) Data Visualization
c) Specifying Model
d) Model Estimation
e) Accuracy & Performance Evaluation
f) Producing Forecast
다음과 같은 순환구조를 가진다
2. 몇가지 단순한 예측기법
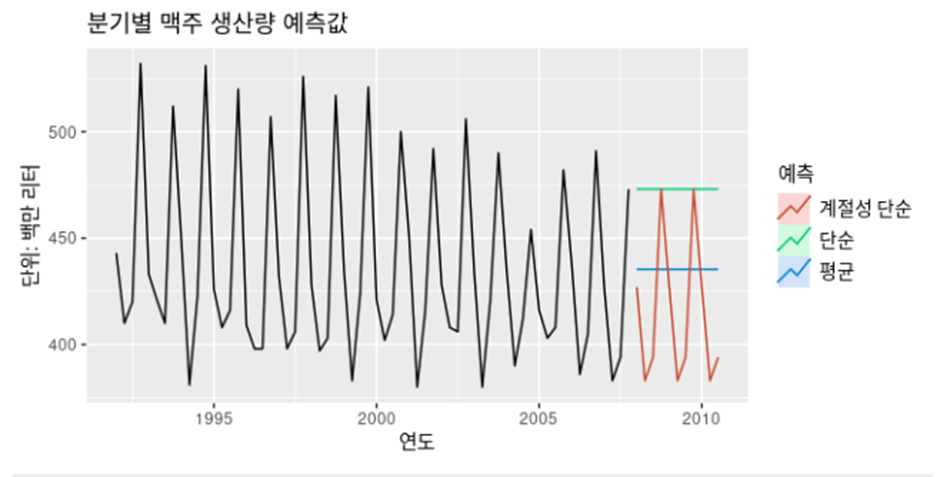
a) 평균기법
미래값이 과거데이터의 평균과 같다
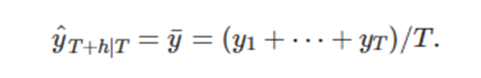
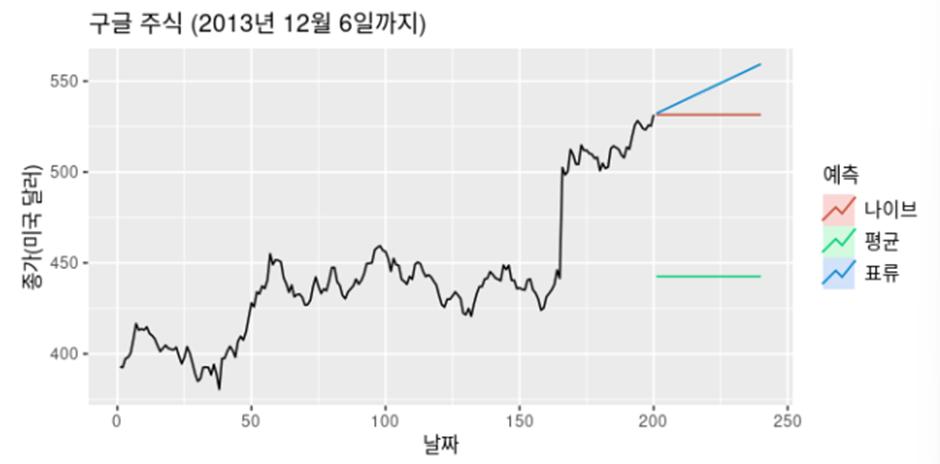
b) 단순 기법 (naïve method)
미래값이 마지막값과 같다(이 방법은 다양한 경제 금융 시계열을 다룰 때 상당히 잘 맞는다)
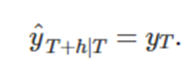
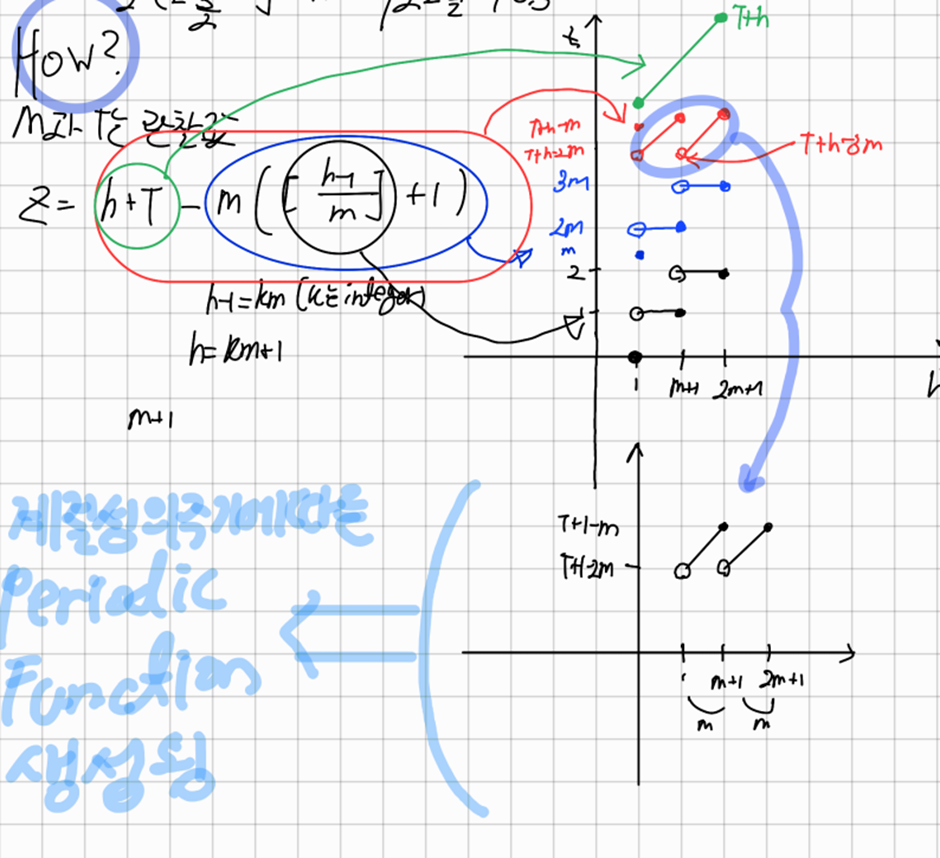
c) 계절성 단순 기법 (seasonal naïve method)
각 예측값을 연도의 같은 계절의 마지막 관측값으로 둔다(계절성이 뚜렷한 데이터에 대해 잘맞음)
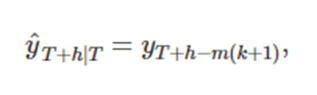
이때 k = [(h-1)/m]+1이고 [ ]는 가우스 기호를 나타내고 m은 계절성의 주기를 나타낸다
참고)
표류기법(Drift Method)
단순기법을 수정하여 예측값이 시간에 따라 증가하거나 감소하게 할 수 있다
시간에 따른 변화량(drift)를 과거 데이터에서 나타나는 평균 변화량으로 정한다
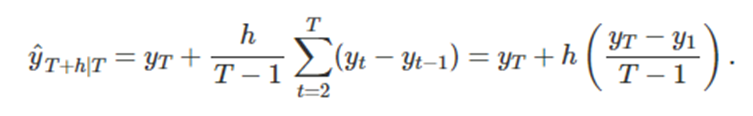
3. 분해를 통한 예측
분해가 주로 시계열 데이터를 연구하거나 시간에 따른 변화를 살펴볼 때 유용하지만 예측에도 사용할 수 있다
덧셈분해
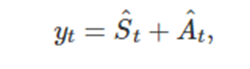
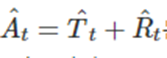이는 계절성으로 조절된 성분을 의미한다
곱셈 분해
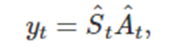
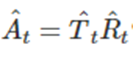
이는 계절성으로 조절된 성분을 의미한다
우리는 S(hat)_t와 A(hat)_t를 각각 예측해야 하는데 S(hat)_t는 나이브 계절성 기법을 사용하고
A(hat)_t와 같은 것은 앞으로 배울 표류를 고려하는 확률보행 모델과 홀트의 기법 비-계절성 ARIMA모델을 사용할 수도 있다
이렇게 계절성분과 계절성으로 조절된 성분을 따로 예측하고 다시 합쳐주는 것을 재계절화라고 한다
4. 잔차(Residual)는 무엇인가
적합값과 잔차는 동시에 설명을 해야한다 예를 들어 우리는 A시점 B시점 C시점에 대한 관측값을 이미 갖고 있다. 이러한 각 관측값을 통해 모델의 매개변수를 추정하고 이 모델을 통해 A시점 B시점 C시점에 대해서 예측값을 낼 수 있다 이 예측값을 우리는 적합값이라고 하고 이 실제값에서 이 적합값을 뺀 값을 잔차라고 한다
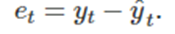
예를 들어 평균기법에서 적합값은 관측한 모든 값에 대한 평균이고
표류 기법에선 모든 관측값을 가지고 표류매개변수
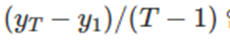
를 추정한다
우리는 이미 관측한 값을 예측한 적합값은 진정한 예측치가 아니다
잔차는 시계열 모델에서 모델을 맞추고 남은 잔차(Residuals)라는 의미와 시계열 모델에서 관측값과 적합값의 차이를 의미하는 잔차(residual) 두가지의 의미가 있다
우리는 모델을 잘 만들었을 경우 다음과 같은 특징을 갖는 잔차(residual)을 낼 것이다
1. 잔차에는 상관관계가 없다 만약 잔차 사이에 상관관계가 있다면 잔차에는 예측값을 계산할떄 사용해야 하는 정보가 남아있는 것이다
2. 잔차의 평균이 0이다 잔차의 평균이 0이 아니라면 예측값이 편향 될 것이다.
( 예측값이 편향되다 -> 예측값들이 정답을 잘 맞추지 못할 것이다)
3. 잔차의 분산이 상수이다 -> 이성질은 예측구간을 계산하기 쉽게한다
4. 잔차가 정규분포를 따른다 -> 만족하지 않을경우 Box-Cox변환을 통해 만족시킬 수 있다
Review) 백색잡음
백색잡음은 추세, 계절성, 자기상관성 등의 시계열적 특성이 모두 제거된 데이터를 말한다
결국 더 이상 모델링 할 수 없는 시계열의 데이터로 값 예측이 불가능하고 랜덤하게 발생되는 값이다. 백색잡음의 특징은 평균이 0이고 분산이 상수로 고정 돼있으며 uncorrelated 해야한다
모델링이 잘된 모델에서는 이 잔차가 곧 백색잡음이 된다 만약 아니라면 잔차안에 모델링에 사용될 정보가 남아있다고 볼 수 있다 우리는 위에서 백색잡음임을 판정할 때 배운 ACF를 사용 할 수도 있지만 좀더 정량화된 test를 알아 볼 것이다.
5. 잔차가 white noise임을 판단하는 방법
잔차가 white noise임을 밝히는 portmanteau 검정들을 알아 보기전에 우리는 귀무가설과 대립가설 그리고 카이제곱분포와 검정에 대해서 알아볼 필요가 있다
5-1. 귀무가설과 대립가설
귀무가설은 통계학적인 증명에서 우리가 증명하고 싶은것에 정확히 반대되는 가정이다 이를 기각하면서 우리는 우리가 증명하고 싶은걸 채택하는 경우를 많이 사용하는데 여기서 증명하고 싶은 가설이 대립가설 기각하는 가설을 귀무가설이라고 한다
5-2 카이제곱분포와 검정
우리는 자유도에 대해서 이해해보자 자유도는 표준정규분포에서 어떤 sample을 뽑는 개수라고 이해하면 된다 여기서 뽑힌 확률변수들을 X1,X2,,,,Xk라고 할 때 자유도 k의 카이제곱 분포는 Q= X1^2+,,,+Xk^2의 분포가 자유도 k인 카이제곱 분포를 따른다고 정의한다. 실제로 표준정규분포에서 sample을 자유도 만큼 뽑아 제곱합한 것의 값의 분포는 카이제곱분포를 따른다고 한다
보통 오차나 편차를 정규분포로 모델링하기 때문에 카이제곱분포는 오차나 편차를 분석할 때 도움이된다
카이제곱 통계량을 이용한 귀무가설의 검정
즉, 검정 통계량 Q가 카이제곱분포표에서 신뢰수준에 따른 χ^2(자유도)_(신뢰수준)[Critical Value] 의값보다 작으면 가설을 채택하고 크면 기각한다
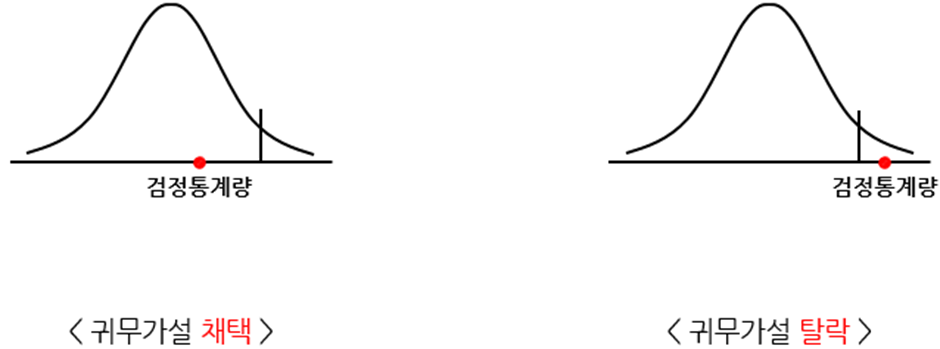
5-3. 잔차에 대한 박스 피어스 검정과 융박스 검정
포트맨토(portmanteau)검정이란 처음 l개의 잔차의 자기상관과 white noise와 의미있게 다른 지 여부를 점검한다 포트맨토 검정안에 박스-피어스(Box-Pierce) 검정과 륭박스 검정(ljung-box)등이 있다
박스-피어스 검정(Box-Pierce)
만약 r_k가 0에 가깝다면 Q는 작을것이다
이 박스-피어스 검정에서 사용하는 검정통계량(Q)은 모델의 매개변수의 개수인 K에 대해서 ( l-K )[시차의수]의 자유도를 가지는 카이제곱 분포를 따를 것이다
왜냐하면 박스-피어스 검정의 귀무가설이 자기상관이 없는 white noise라는 것이기 때문에 r_k는 정규분포를 따르고 이때 r_k는 정규화과정을 거쳤기 때문에 분산이 1로 바뀐다
따라서 상관관계를 평균이 0이고 표준편차가 1인 표준정규분포에서 뽑은값이라고 볼 수 있는것이다
융-박스 검정(ljung-Box)
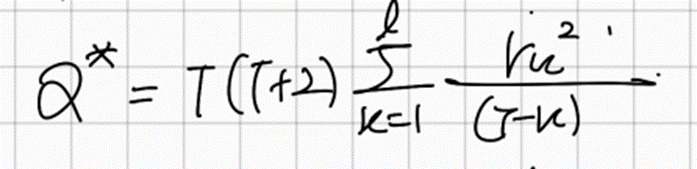
융-박스 검정은 박스-피어스 보다 더 정확한 검정이다
융-박스 검정에서 사용하는 검정통계량 또한 ( l-K )[시차의수] 자유도를 가지는 카이제곱 분포를 따른다
그렇다면 위의 Q^*와 Q 통계량을 이용해 어떻게 잔차가 white noise 임을 판정할 수 있을까
( l – K )의 자유도를 가지는 카이제곱 분포에서 95퍼센트 신뢰수준의 Critical Value인
χ^2( l – K )_(0.95) 보다 Q의 통계량이 작을경우 귀무가설을 채택해서 White Noise이고 크면 White Noise가 아니게 된다 즉, 잔차간의 상관관계가 존재하게 된다
6. 예측분포와 예측구간
예측오차(ForeCasting Error)와 잔차(residuals)의 차이점;
예측오차와 잔차는 시점의 문제다 우리는 이미 관측된 값으로 모델을 만들고 관측시점에 예측값을 만들어낸다 이때의 관측값과 예측값의 차이가 잔차이고 이 모델을 통해 앞으로의 시점에 대해서도 예측 할 수 있다 이때 시간이 지나면서 관측값이 생기고 이 관측값과 예측값의 차이가 예측오차( ForeCasting Error )이다
6-1.예측기법 별로 h 단계 예측분포와 그 표준편차
y ̂_(T+h|T) 은 y_1,y_2, … ,y_T가 주어졌을 때 y_T+h 분포의 평균값 즉 point forecast이다
예측구간(Prediction Interval, PI)는 특정한 확률로 확률변수가 들어갈 구간을 의미한다
예측오차(forecasting error)가 상관관계가 없고 정규분포를 따른다고 가정하면
우리는 위의 h-단계 예측값에 대한 95% PI를 다음과 같이 쓸 수 있다
더 일반적으로 적으면 다음과 같이 쓸 수 있다
예측구간의 값은 예측값의 불확실성을 나타낸다 만약 점예측값만 낸다먼 예측값이 얼마나 정확한지 나타낼 방법이 없다 따라서 불확실성의 측정없는 점예측값은 의미가 없다
우리는 위에서 기본적인 예측기법 별로 예측값에 대해서 알아봤다 따라서 우리는 각 기법별로
예측값의 정규분포를 구할수 있다 ( σ ̂ :잔차의 표준편차 )
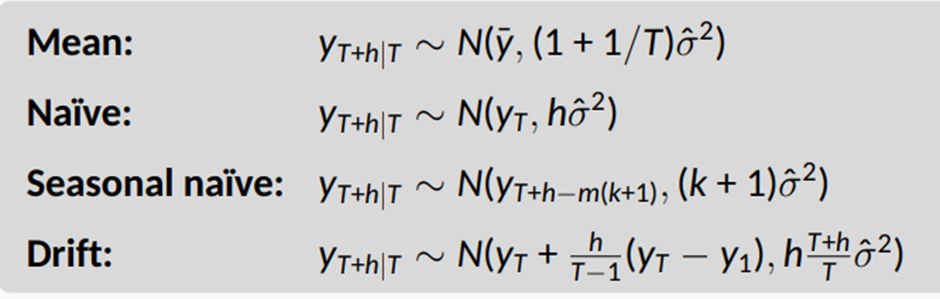
6-2. 한단계 예측구간과 여러 단계 예측구간
위 정규분포의 표준편차는 잔차의 표준편차 σ ̂ 로부터 유도 됐다 h=1이고 T가 충분히 크다면 위의 모든 값은 같은 근사값인 σ ̂ 로 근사된다
한단계 예측구긴의 표준 편차는 잔차의 표준편차와 같다고 추정하는게 좋은 추정치가 될수있다
여러단계 예측구간에서는 위의 표준편차로 볼 수 있듯이 예측 범위(h)가 증가할수록 PI가 길어지는것을 볼 수있다 즉, 더 먼미래를 예측할수록 예측에 불확실성이 커지고 예측구간이 넓어진다
6-3. Box-Cox의 역변환
우리는 위에서 Box-Cox변환으로 얻은값을 통해 예측값을 얻었다. 하지만 이는 데이터의 level을 바꿔서 얻은 값이길래 다시 back transformation을 시켜주어야할 필요가 있다.
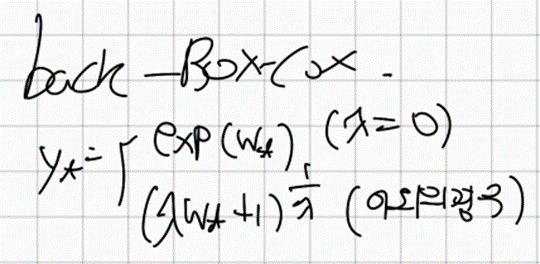
6-4. 역변환으로 생긴 중간값의 편향 조정하기
이렇게 해서 얻은값은 보통은 데이터 예측구간의 평균이 아닌 중간값이 되는 경우가 많다
이렇게 역변환된 중간값과 평균사이에 생기는 차이를 편향(bias)이라고 한다
편향 조정은 Second order Taylor Expansion을 이용하는데 다음과 같다
6-5. 예측정확도 평가하기
예측오차를 사용해서 정확도를 측정한다
여기서는 정확도를 측정하는 방법론에 대해서 알아볼 것이다
Scale-dependent Measure) MSE, RMSE, MAE
Scale에 의존하는 측정방법은 한가지 시계열의 여러가지 모델을 비교하는 경우 또는 같은 scale을 가진 여러 시계열을 비교하는 경우에 사용 될 수 있다
위의 정확도 평가 방법은 단위가 맞지않는 시계열 데이터에 대해서 모델의 정확도를 비교하는데는 적절치 않다는 단점이 있다 이를 개선한 것이 바로 백분율 오차(Percentage Error)이다
백분율 오차(Percentage Error) MAPE (Mean Absolute Percentage Error)
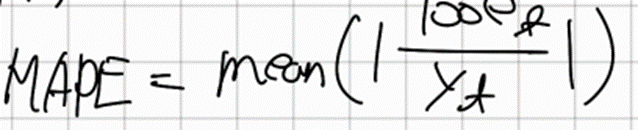
이는 예측오차를 예측값으로 나누면서 Scaling을 했다
따라서 단위와 관련이 없다는 장점이 있다
하지만 만약 예측값이 0을 갖는다면 diverge되거나 정의되지 않는 문제가 발생한다
이러한 문제의 대안으로 MASE가 존재한다
Hyndman, R. J., & Koehler, A. B. (2006). Another look at measures of forecast accuracy. International Journal of Forecasting, 22(4), 679–688. [DOI]
MASE(Mean Absolute Scaled Error)
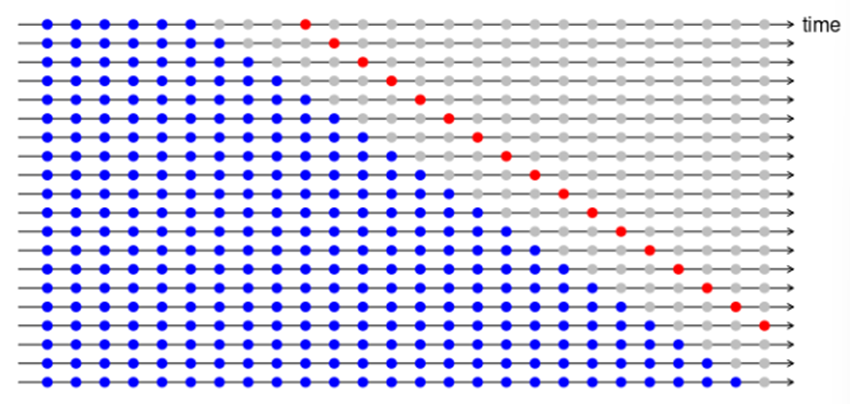
이는 naïve forecast 의 MAE에 기초해서 오차의 scale을 조정하는 방법을 제안했다(q_j 눈금이 조정된 오차)
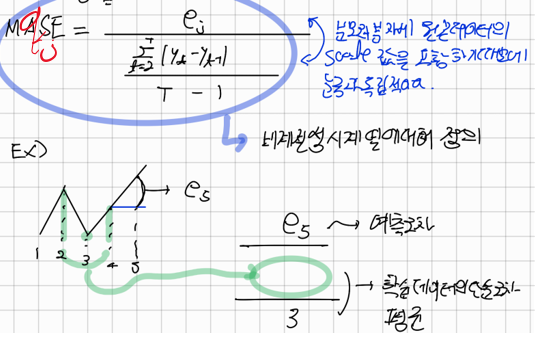
- q_j 이다
만약 예측오차가 학습데이터의 단순오차 평균보다 좋은 예측치를 냈다면 1보다 작고 아닌경우 1보다 크다
계절성 시계열에 대해 Scale이 조정된 오차는 Snaïve forecast 를 사용해서 정의된다
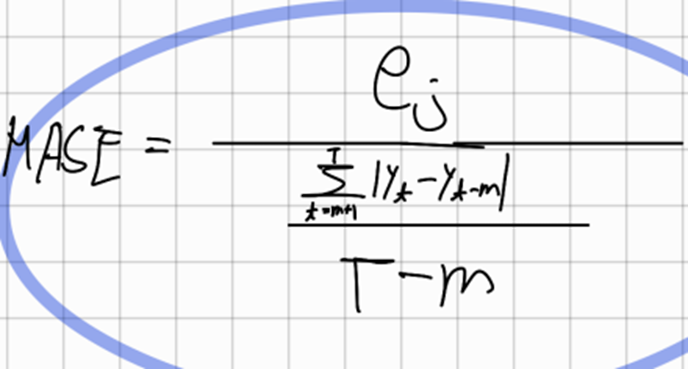
이렇게 눈금이 조정된 오차에 대해서 MAE를 실시한다
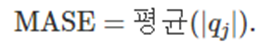
Cross-Validation
우리는 예측 정확도를 위에 같은 방법을 활용해서 구할 수 있지만 우리는 다른 M.L 모델을 평가하는 방법중에 교차검증이라는 것을 알고있다 교차검증을 통해 얻을수 있는 장점은 데이터의 모든부분을 학습에 사용한다는 점이고 이를 통해 학습데이터가 적을때는 어느정도 개선이 가능하다 또 데이터를 계속해서 바꿔주기 떄문에 overfitting이 생길 가능성이 적어진다
이러한 cross-validation이 시계열에도 존재하는데 조금 다른 방식으로 존재한다
시계열의 cross-validation에서는 시간에 따라 테스트의 지점을 미래로 굴려서 얻은 예측을 평가한다 그걸 평균을 내서 정확도를 판정한다 이러한 방식 때문에 evaluation on a rolling forecasting origin이라고 하기도한다 이는 multi step forecasting에서도 그대로 적용된다
[multi step]
Linear model with time series
1. 단순선형회귀와 다중선형회귀
회귀에서는 예측변수의 매개변수를 찾는 것이 목표이다
단순선형회귀
-> 단하나의 예상 변수 y와 하나의 예측변수 x 사이의 선형관계를 다룬다
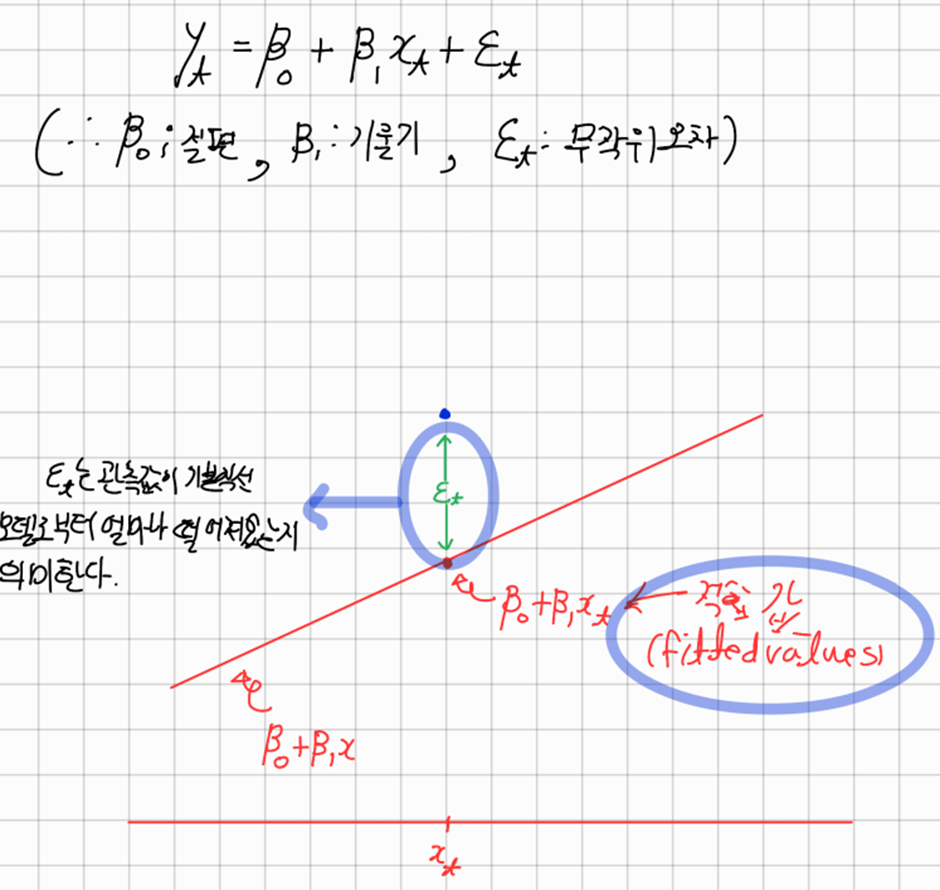
다중선형회귀
-> 두개 이상의 예측변수가 있을 때, 모델을 다중회귀모델이라고 한다
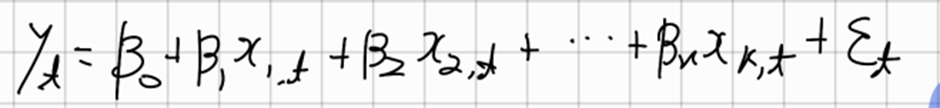
여기서 계수는 모델에서 다른 모든 예측변수의 효과를 고려한 후의 각 예측변수의 효과를 나타낸다 (내생각: 가중치를 둔다)
선형회귀모델을 사용할떄 오차에 대해 다음과 같은 가정을 사용한다
1. 오차의 평균은 0이다
2. 오차는 자기상관관계가 없다
3. 오차는 예측변수와 상관관계가 없다; 만약 있다면 모델에 포함되어야할 정보가 더 있을수 있다
4. 오차가 일정한 분산값을 가지는 정규분포를 따른다
즉, 오차가 백색잡음이다
2. 예측변수로 설정하면 유용한것들
추세
-> 시계열 데이터에서 추세가 나타나는 것은 흔한일이다
선형추세는 단순히 t 를 예측변수로 사용하여 모델링 할 수 있다
추세가 계속될 때 t를 예측변수로 사용하는 것은 강력한 가정이다
가변수(Dummy variable)
만약 예측변수가 categorical한 변수일 경우에는 어떻게 할까 이경우에는 모델에 가변수(1또는 0의 값 만을 가짐)를 추가해주면 된다
계절성 가변수
일별 데이터를 예측하고 있고 요일을 고려하고 싶다고 하자. 그러면 다음과 같은 가변수를 만들 수 있다
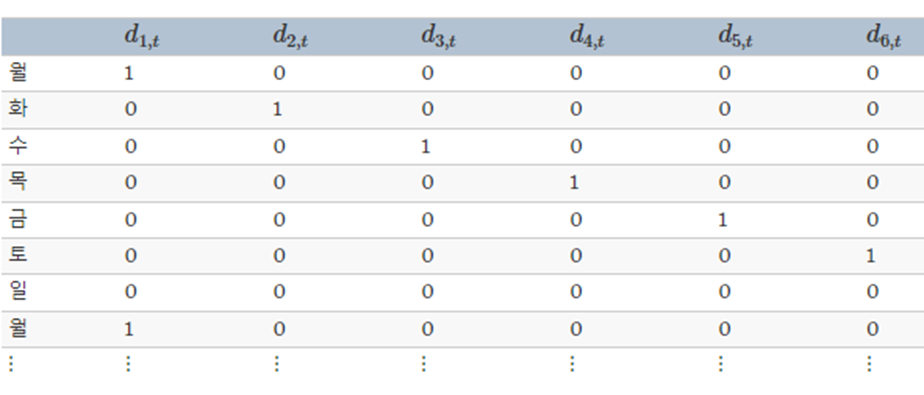
7개의 변수를 나타내기 위해 6개의 가변수를 만든 것을 보자 왜 굳이 가변수 하나를 덜 썼을까?
이를 알기 위해선 우리는 기본적으로 회귀모델의 매개변수를 추정할 때 최소제곱법을 사용한다
하지만 만약 여기서 가변수를 하나 더 만들어주게 될 경우 최소제곱법에서 역행렬을 만들 수 없는 상태가 되는데 뒤에서 알아보겠다 이를 가변수함정(Dummy Trap) 이라고 한다
가변수 함정을 피하기 위해서는 기준이 되는 값을 정하고 이를 0벡터로 지정해야한다
따라서 분기별 데이터는 3개의 가변수 월별데이터는 11개 일별 데이터는 6개의 데이터를 사용한다
개입변수(intervention variable)
예측하려는 변수에 영향을 줄 수도 있는 개입값을 모델링 하는 것이 필요하다 예를들어 경쟁자의 활동, 광고지출, 산업변화 등이 있다
효과가 한 주기만 지속될때는 스파이크(spike)변수를 사용한다 이것은 개입기간에만 1로 두고 그외에는 0으로 두는 가변수이다.
만약 영구적인 개입이라면 개입전에는 0으로 두고 개입이 시작되고 나서는 1로 바꾼다
3. 회귀 모델 비교
a) R^2(결정계수)
결정계수는 예측변수(독립변수)가 예상변수(종속변수)를 설명하는 정도를 나타낸다
예를들어 R^2=0.3이면 예측변수가 예상변수의 30%정도를 설명한다고 얘기한다
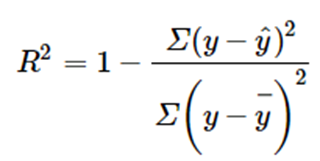
하지만 R^2의 치명적인 단점은 자유도를 반영하지 않는다는 것이다 즉, 모델에 적합하지 않은 예측변수라도 일단 추가하면 올라가는 경향이있다
이러한 이유 때문에 조정된 결정계수(R-bar-squared)가 나왔다
'
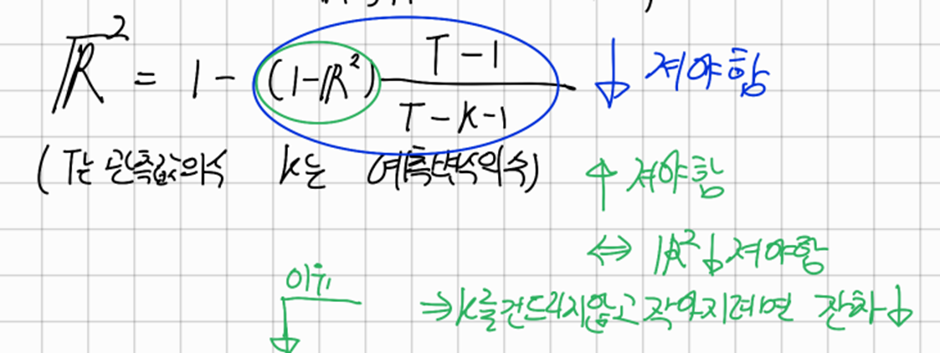
조정된 R^2을 최대화하는 방법은 결국 R^2을 최대화하는 것과 같다 그렇다면 결국 잔차의 합(SSE)을 최소화 하는 것과 같은데 따라서 잔차의 표준편차라고 정의되는 표준오차를 최소화 하는것과 같다 이때 우리는 자유도의 개념과 함께 표본표준편차를 구할 때 왜 n이 아닌 n-1을 나누는지에 대해서 생각해 볼 필요가 있다
출처: https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=jindog2929&logNo=10183165564
요약하자면 자유도란 데이터가 갖고 있는 정보량인데 이 정보량 이란게 쓸수록 사라진다
또 표본표준편차에서 나누는 n-1은 자유도를 의미하는것이다
우리의 선형회귀 모델의 매개변수는 k+1개이다 이때 매개변수 하나를 추정하는데 T구간에 있는 정보를 사용한다고 보면 된다 따라서 자유도는 T-k-1인것이고 이를 나누게 되는것이다
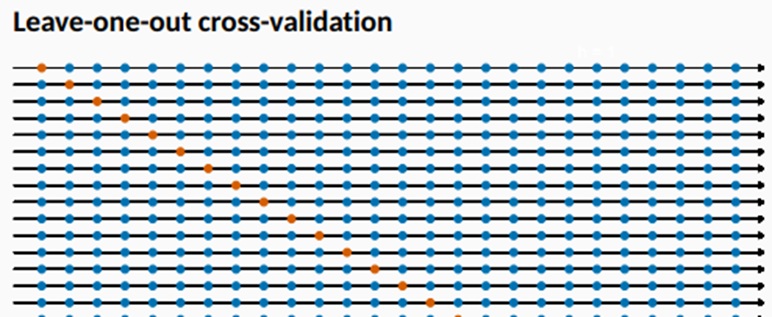
일반적인 cross-validation의 변형(leave-one-out 교차검증)
[단일 관측치를 빼는 교차검증]
맨 처음 시간부터 데이터를 하나씩 빼고 남은 데이터로 학습한후 뺸 시간의 데이터를 예측한다
이 예측값과 관찰값의 차이를 e_t^*=y_t-y ̂_t 라고 정의하고 예측할 때 테스트 데이터의 시점을 사용하지 않았으므로 잔차는 아니다
이 차이를 t=1,2, … T까지 하고 MSE를 계산한다.
Tip) 회귀에선 leave-one-out cross validation이 더 빠르고 효과적이다
[복잡한 모델과 덜 복잡한 모델의 비교]
AIC(Akaike Information Criterion)
AIC는 모델들끼리 비교하는데, 엄청나게 복잡하지만 약간 좋은 성능을 가진 모델과 성능은 떨어지지만 간단한 모델을 비교하기 위해 사용되는 변수의 수를 감안함으로써 패널티를 부여한다
AIC의 값이 최소인 모델이 가장 좋은 모델이 된다
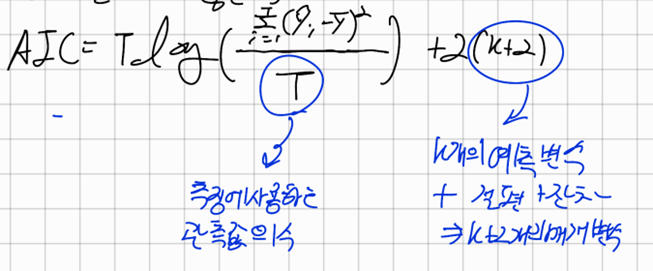
하지만 T가 작다면 AIC는 예측변수의 개수에 의존하는 경향이 있다.
따라서 최근에는 수정된 AIC인 AICc를 사용한다
AICc
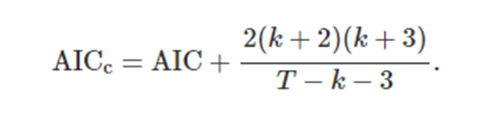
BIC(Bayesian Information Criterion)
-> AIC와 매우 비슷한데 뒤에 예측변수 에 log(T)를 곱해줌으로써 예측변수의 수에 더큰 패널티를 준다
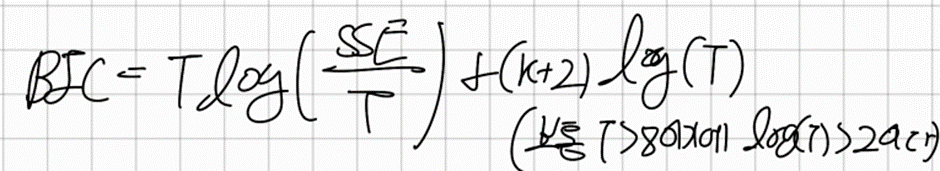
이렇게 우리는 모델간의 비교 방법을 알아봤다
하지만 가장 좋은 방법은 그냥 다 맞춰보고 측정량이 제일 좋은걸 고르는 것이다
하지만 예측변수가 44개면 가능한 모델은 18조개가 된다
이렇게 많은 모델을 비교하는건 사실상 불가능 하고 모델의 개수를 제한하는 방법이 있다
Backwards stepwise regression
(Top to Bottom)
Forwards stepwise regression
(Bottom to Top)
4. 예측의 종류
사전 예상값(ex-ante forecast)
-> 미리 쓸 수 있는 정보만으로 값을 내는 진정한 의미의 예측값이다
이 예측값들은 예측변수들의 예상값이 필요하다 이는 과거~현재까지의 값의 평균이나 정부기관에서 발표하는 예상값 같은 정보를 쓰는등 다양한 방법이 있다
사후 예상값(ex-post forecast)
-> 예측변수의 실제값을 관측하고나서 이 관측값을 이용해 예측한다
-> 사후 예상값은 예측변수에 관한 지식은 사용할 수 있지만 예측할 데이터(y변수)에 대한 지식을 추세나 계절성으로 가정하면 안된다
시나리오 기반 예측
-> 예측하는 사람은 관심있는 예측변수에 대해서 지정하고 관심있는 결과에 대해서 예측을한다 따라서 예측구간에서는 예측변수의 미래값과 관련된 불확실성이 없다
Ex> 금리가 0.5퍼센트,1퍼센트 올랐을때와 0.5퍼센트,1퍼센트 내렸을때의 예적금 고객수에 대해서 예측하고자 할 때
시나리오 기반 예측
-> 예측하는 사람은 관심있는 예측변수에 대해서 지정하고 관심있는 결과에 대해서 예측을한다 따라서 예측구간에서는 예측변수의 미래값과 관련된 불확실성이 없다
Ex> 금리가 0.5퍼센트,1퍼센트 올랐을때와 0.5퍼센트,1퍼센트 내렸을때의 예적금 고객수에 대해서 예측하고자 할 때
예측 회귀 모델 세우기
회귀모델로 예측을 하기 위해서는 사전예측 같은 경우에는 예측변수의 미래값이 필요하다 시나리오 기반의 예측에서는 괜찮을 수 있다
대안으로써는 예측변수로 시차값을 사용하는 것이다 h 단계 앞 예측을 내는데 관심이 있다고 하면 현재값을 포함해 과거의 h주기에 관찰한 x값으로 예측변수가 구성되는 것이다
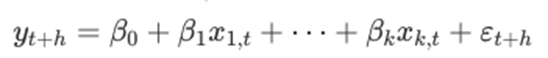
[단순회귀의 예측구간]
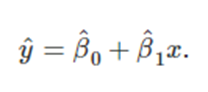
회귀오차가 정규분포를 따른다고 하면 예측구간은 아래처럼 계산한다
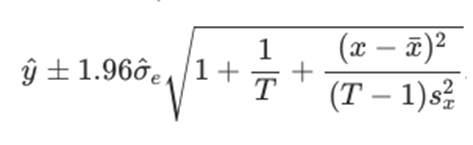
5. 상관관계와 인과관계
-> 상관관계와 인과관계를 혼동하지 않는 것은 중요하다 즉, x가 y를 예측할 때 유용할 수는 있지만 이것이 x가 y의 원인이라는 것은 아니다
-> Ex> 해변의 익사사고와 아이스크림의 개수
해변의 익사사고횟수와 아이스크림이 팔린 개수를 살펴보면 어느 정도의 상관관계가 있어보이고 실제로 모델링을 할 수 잇다 하지만 익사사고와 아이스크림의 개수는 인과관계가 아니다
실제로는 기온이 원인인데 이렇게 제3의 변수가 종속변수(익사사고 횟수)와 독립변수(아이스크림이 팔린 개수) 둘 다 한테 영향을 줄 때 우리는 이를 혼선자(confounder)라고 부른다
#하지만 상관관계는 혼선자나 인과관계가 있더라도 예측에 용이하다는 것을 인지하고 있어야한다
6. 다중공선성(multi colinearlity)
다중 회귀에 2개이상의 예측변수로 비슷한 정보가 주어질 때
이것에 의미는 두 예측변수(한 예측변수와 다른 예측변수들의 조합간)의 상관관계가 -1 혹은 +1에 근접하게 높을 때를 의미한다
가변수 함정은 다중공선성의 특별한 경우이다
분기별 데이터에 대해 4개의 가변수를 사용하면
d_4=1-(d_1+d_2+d_3)가 성립하고 이는 그래프를 그려보면 d_4와 d_1+d_2+d_3간의 완벽한 상관관계가 있음을 알 수 있다
다중공선성은 쓸데없이 모델을 복잡하게 만들어서 제거해줘야 한다
[부록] Ordinary Least square
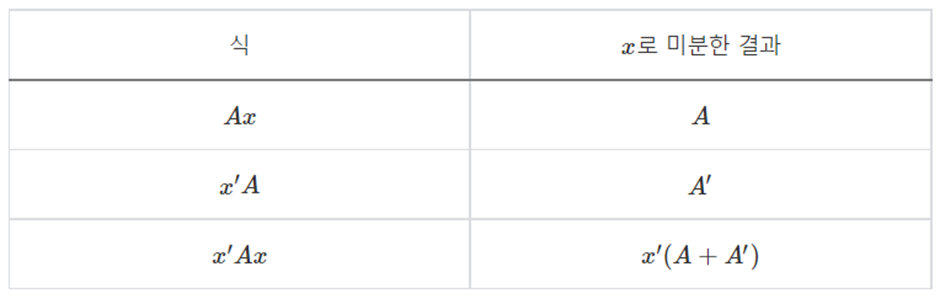
‘ = Transpose
Ex> 여기서 만약 월요일 화요일 수요일을 나타내는 dummy variable을 3개를 쓴다고 가정해보자
그러면 X=[[1,1,0,0],[1,0,1,0],[1,0,0,1]]이 될 것이다 이를 계산해보면 rank때문에 X^T X의 역행렬이 생기지 않는다
