내용 출처:
Likelihood: https://www.youtube.com/watch?v=mxCmB1WE3R8
전반적인 내용 및 사진 출처:
https://otexts.com/fppkr/

개요

1. What is smoothing?

• 가. 평활법이란, 평활을 사용할 때
• 나. SMA(simple moving average)의 단점

2. Simple/Double/Triple Exponential Smoothing

• 가. 단순지수평활
• 나. 이중지수평활
• 다. 홀트-윈터스의 계절성 기법
• 라. 이외에 사용가능한 모델

3. ETS model

• 가. ETS model과 상태공간모형(State Space Model)
• 나. 가능도와 모델선택
• 다. ETS모델로 예측하기

1. What is smoothing

가. 평활법이란(smoothing method), 평활을 사용할 때

시간에 따라 수집된 데이터에는 무작위적인 변화량이 있다
여기서 평활(smoothing)이란 이렇게 무작위적 변화로 생기는 효과를 줄이는 방법들중 흔히 사용되는 기법이다 예를들어 주어진 시계열 자료에 평균을 취하는 것은 단순한 평활법이다 평균은 과거 관측값을 동일한 가중치로 다루기에 추세가 존재하면 좋은 지표가 될 수 없다 평활을 이용해서 시계열을 세가지 성분으로 분해하거나, 예측을 수행할 수 있다
여기서는 주로 예측에 포커싱이 돼있다

나. SMA(simple moving average)의 단점

1. 단순이동평균을 사용하면 이동평균기간만큼 시차가 생긴다
2. 단순이동평균은 그저 추세만 보여줄 뿐이지 실제 미래변동에 관한 어떤 정보도 담고 있지 않다
3. 이상치에 쉽게 왜곡된다
4. 과거데이터와 현재데이터에 같은 가중치를 두고있다

example>

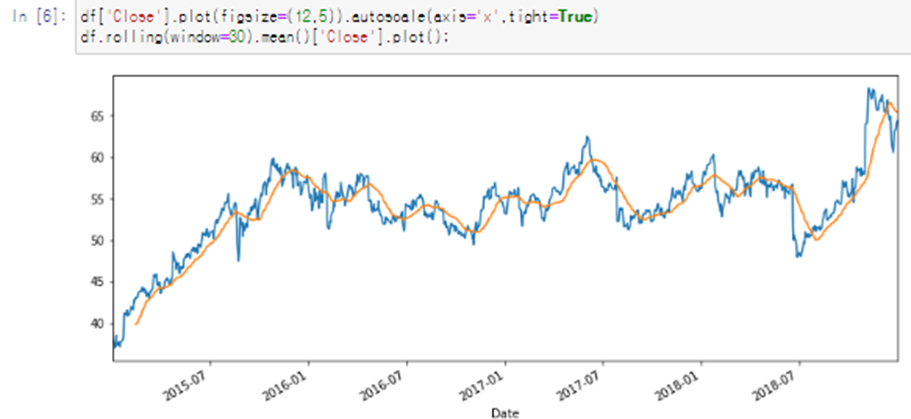
2. Simple/Double/Triple Exponential Smoothing

지수평활 (exponential smoothing)

지수 평활을 사용하여 얻은 예측값은 과거 관측값에는 적은 가중치를 두고 최근 관측값에는 많은 관측치를 두어서 효과적으로 예측 할 수 있게 한다
시계열 자료는 시간의 흐름에 따라 장기간에 걸쳐 관측되는데 시간에 따라 관측한다는 점이 어느시점의 큰사건으로 인해 모형이 잘 안 맞을수도 있다 따라서 이러한 변화를 잘 받아들이기 위해 최근의 자료일수록 더 높을 가중치를 두어 최근의 경향을 반영토록 한것이다

가. 단순지수평활(simple exponential smoothing,SES)

이방법은 추세나 계절성 패턴이 없는 데이터를 예측할 때 쓰기 좋다

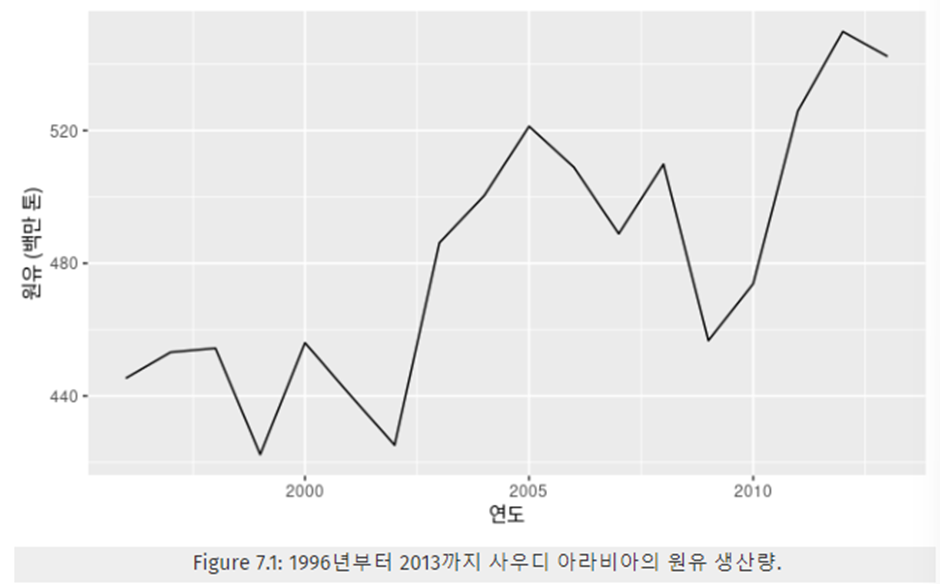
단순기법(naïve method)은 가중치를 마지막 값에만 할당했다고 볼 수 있고
평균기법은 가중치를 모든 데이터에 동등하게 할당했다고 볼 수 있다
하지만 단순지수평활(Simple Exponential Smoothing)은 오래된 관측값보다 최근에 값에 더 큰 가중치를 준다

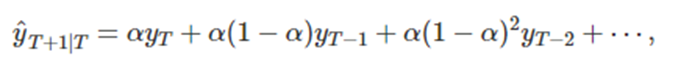
여기서 0<=alpha<=1은 평활매개변수이다 0<=(1-alpha)<=1 이므로 오래된 관측값에 더 작은 가중치를 부여 하는 것을 알 수 있다.
관측값에 붙는 관측치가 과거로 갈수록 지수적으로 감소해서 exponential smoothing이라는 이름이 붙었다 alpha가 크면 더 먼과거에 붙는 가중치가 크고 alpha가 작으면 더 최근 관측값에 붙는 가중치가 늘어난다

단순지수평활의 성분형태(표현방식의 차이)

-> 성분형태는 예측식과 평활식으로 구성된다
수준값($l_t$=level):
level은 Trend와 Seasonallity를 뺀 순수한 값의 수준이라고 생각하면 된다

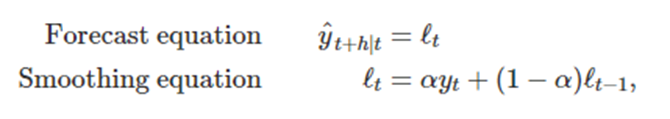
최적화(Optimization)
모든 지수 평활법을 응용할 때 평활 매개변수와 초기값이 필요하다
특히 단순 지수평활의 경우 alpha와 $l_0$값을 선택해야하는데 이전의 경험에 근거해서 평활매개변수를 정할수도 있지만 관측된 데이터에서 추정하는 것이 더욱 객관적일 것이다
잔차(t=1,2,3, .. ,T)에 대해서 $e_t$=$y_t$-$\hat{y}_{t|t-1}$를 최소화하는 매개변수와 초기값을

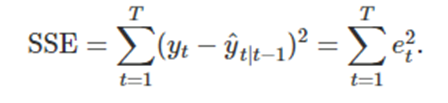
즉 SSE를 최소화하는 alpha값과 초기값을 찾아야한다
--Python--
이를 파이썬 에서는 span(기간) com(질량중심값) halflife(반감기)로 alpha값을 나타내고 가중평균 방법은 pandas의 ewm메소드의 adjust가 true냐 False냐에 따라 달라진다 adjust는 가중치의 불균형을 해소하기 위해 single exponential weight method를 가중평균 한 것이다

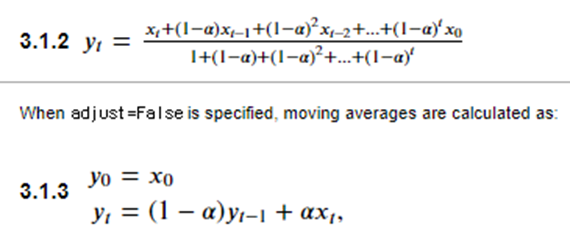
Span: 지수이동평균할 기간으로 alpha 값을 계산한다
또는 직접 alpha값을 입력할수도 있다

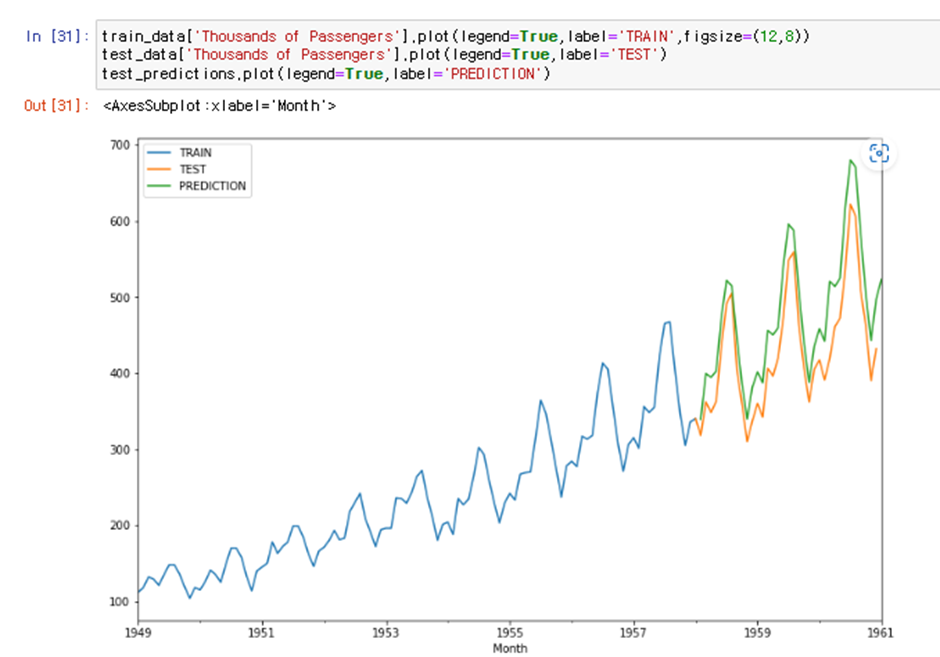
[연도별 airlinepassenger 수]

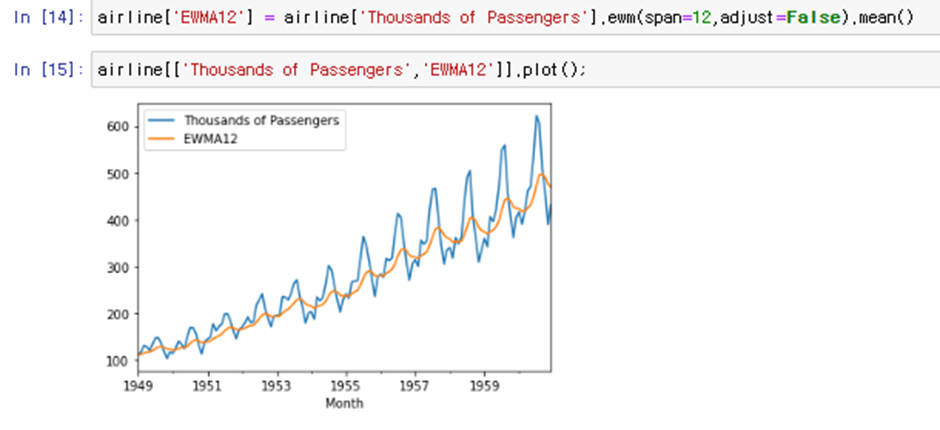
계절성이 시간이 지날수록 더욱 두드러지는데 이는 오래된 자료보다 최신의 자료에 더 큰 가중치를 주었기 때문이다
예제> alpha = 0.83

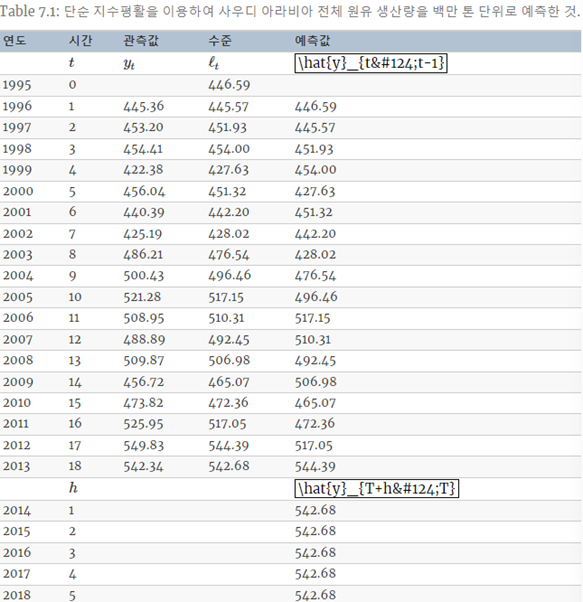
위 예제에서

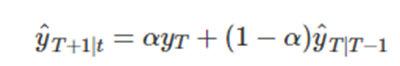
위의 식이 맞아 들어감을 ${\hat{y}}_{T|T-1}=l_{t-1}$을 이용해서 알 수 있다

나. 이중지수평활(Double Exponential Smoothing)(홀트의 선형 추세기법)

추세가 있는 데이터를 예측할 수 있도록 단순 지수 평활을 확장했다 이 방법은 예측식과 두 개의 평활식(하나는 수준에 관한 것, 다른 하나는 추세에 관한 것)을 포함한다

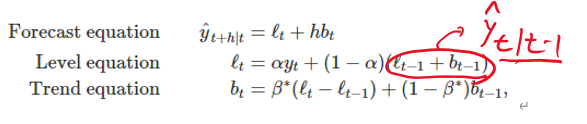
$l_t$는 시간 t에서 시계열의 수준 추정 값, $b_t$는 시간 t에서의 시계열의 추세(기울기) 추정값
$0<=alpha <=1$ 는 수준에 대한 매개변수
$0<=beta^*<=1$ 는 추세에 대한 매개변수를 나타낸다

세번째 평활식(추세식)은 t시점과 t-1시점의 수준차이(평균변화율을 의미)와 t-1시점의 추세를 가중평균한 것이다

${\hat{y}}_{t+h|t}$는 마지막 관측값에 대한 수준값 + 마지막 추세 추정값의 h 배 한 값으로 해석할 수있다

$Alpha$와 $beta^*$ $l_0$, $b_0$는 위에SES 의 매개변수를 정했던것처럼 SSE의 값을 최소화하는 매개변수를 추정한다( Pyhon:
ExponentialSmoothing의 initialization_method(default = estimated)에서 자동추정)

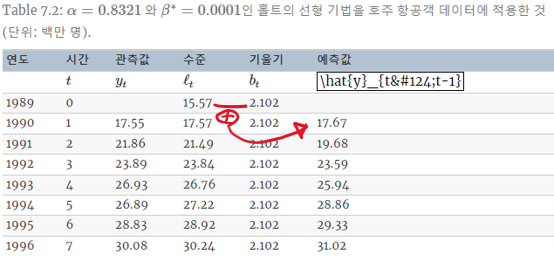
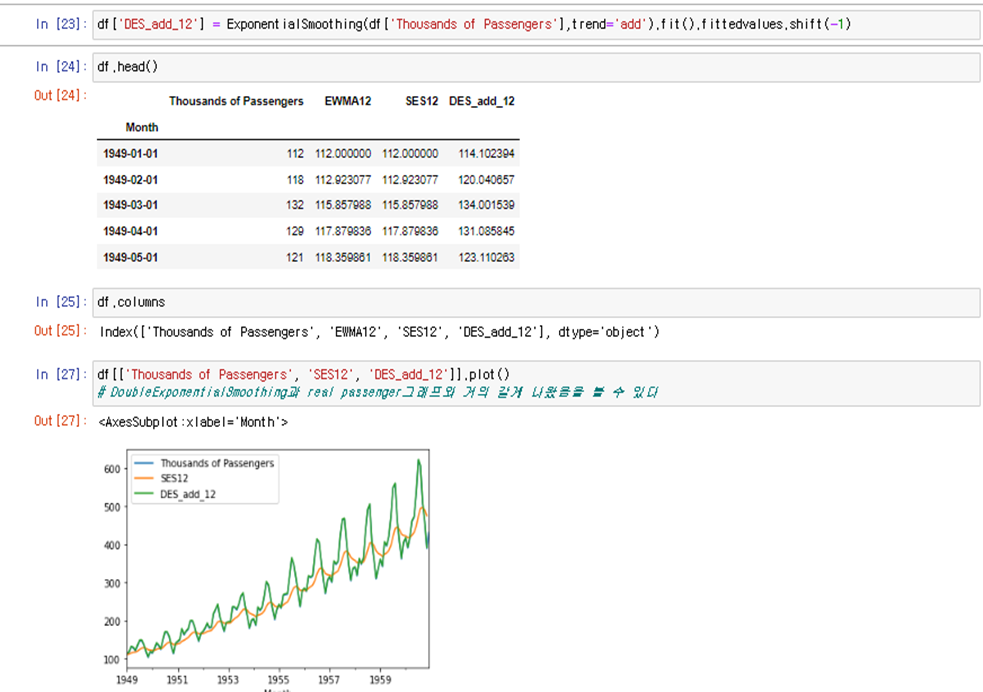
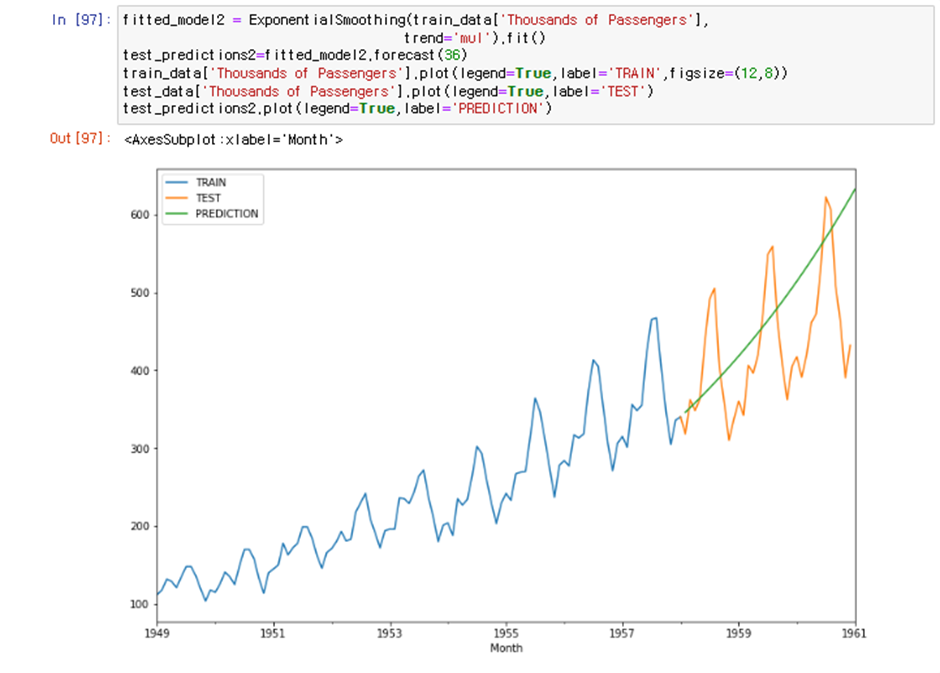
이제부터는 Python statsmodels라이브러리의 ExponentialSmoothing모델을 사용한다
사실 위에 단순이동평균도 statsmodel의 SimpleExpSmoothing을 사용하면 같은값을 낼수있다

감쇠 추세 기법

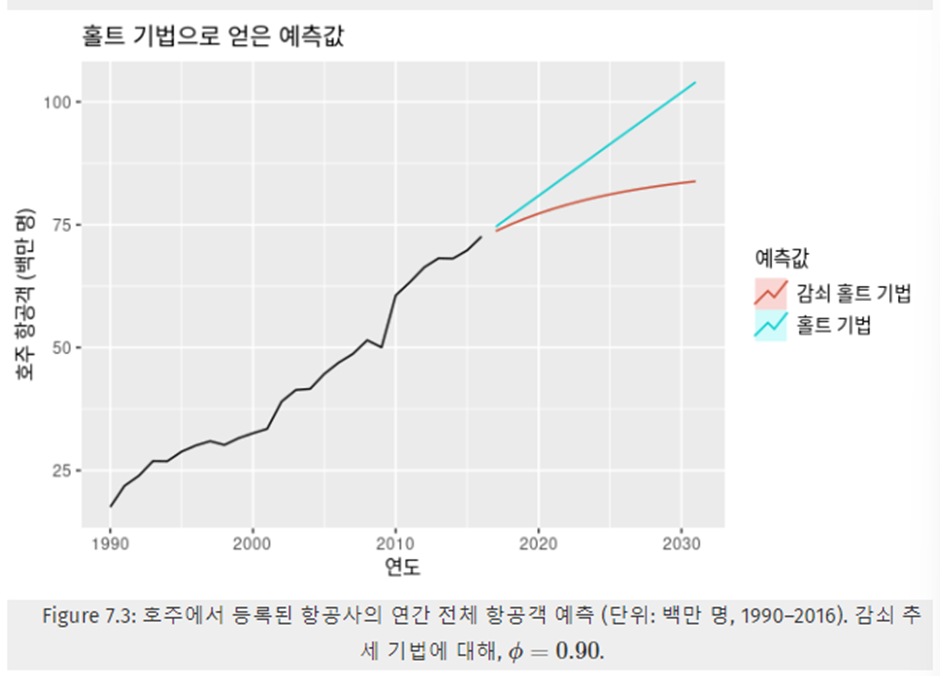
• 홀트의 선형 기법으로 얻은 예측값은 미래에도 계속 일정한 추세(증가 또는 감소)를 나타낸다

• 이러한 문제점을 해결하기위해 Gardner&McKenzie는 미래 어느 시점에 추세를 평평하게 감쇠시키는 한 가지 매개변수를 도입했다
• 감쇠하는 추세(damped trend)를 포함하는 기법은 가장 인기있는 기법이다
  
  
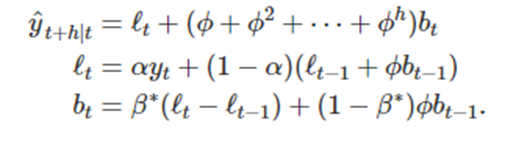
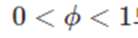
  만약에 $\phi$가 1이면 홀트의 선형 기법과 완전히 같다
  여기서 파이는 추세를 감쇠시켜 미래 어떤 시점에 추세가 상수가 되도록 한다
  하지만 h가 커지면
  
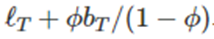
  로 수렴한다

이러한 효과에 의해 단기 예측값은 추세를 반영하고 장기 예측치는 상수가 되어버린다
파이가 작을수록 감쇠 효과가 강하게 들어가기 때문에 실제로는 파이가 0.8보다 작은 경우는 드물다

다. 3중지수평활(Triple Exponential Smoothing)(홀트-윈터스의 계절성 기법)

• 계절성을 잡아내기 위한 기법
• 성분표현은 예측식과 3개의 평활식으로 구성된다($l_t$ , $b_t$ , $s_t$(계절 성분에 관한 것 대응 매개변수는 $gamma$)
• 두 가지 변형이 있는데 덧셈 기법은 계절성 변동이 시계열 전반에 걸쳐 거의 일정할 떄 사용하고, 곱셈 기법은 계절성 변동이 시계열의 수준에 비례하게 변할 때 사용한다
• 덧셈기법에서는 수준식에서 계절성분을 빼서 시계열을 계절성으로 조절하고
• 곱셈기법에서는 수준식에서 계절성분을 나눠서 시계열을 계절성으로 조절한다

덧셈기법>

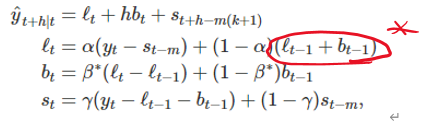
$k=\left[\frac{h-1}{m}\right]$ 이고 m은 계절성의 주기이다

• 수준식은 계절성으로 조정된 관측값과 시간t에 대한 비-계절성 예측의 가중평균을 나타낸다
• 계절성 식은 현재 계절성 지수와 이전연도의 같은 계절의 계절성 지표 사이의 가중 평균을 나타낸다

곱셈기법>

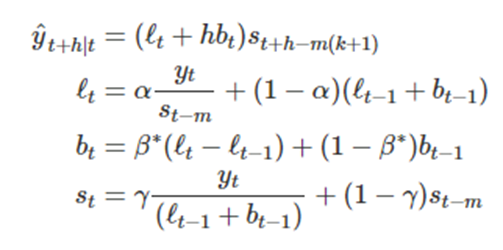
홀트-윈터스의 감쇠기법>

• 홀트-윈터스의 덧셈과 곱셈 기법 두 경우 모두 감쇠 효과를 추가할 수 있다

다음은 홀트-윈터스에 감쇠 추세(damped trend)와 곱셈 계절성(multiplicative seasonality)을 고려한 것이다

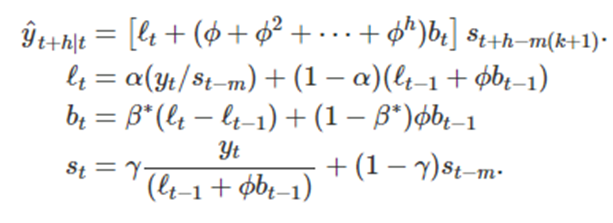
라. 이외에 사용가능한 모델

이들을 조합해서 사용할 수 있는데 추세와 계절적인 성분의 조합을 고려해보면 15개의 지수 평활 기법이 가능한데 곱셈 추세 기법은 나쁜 예상치를 내는 경향이 있어 제외한다
추세성분 : 추세가 선형에 가까우면 trend= add 를 쓰는게 좋고 지수적이나 비선형이면 mul을 사용하는것이 좋다
계절성분 : 계절성이 시계열의 수준에 상관없이 일정하면 seasonal=’add’를 사용하는 것이 좋고
시계열의 수준에 비례하면 seasonal=’mul’을 사용하는 것이 좋다

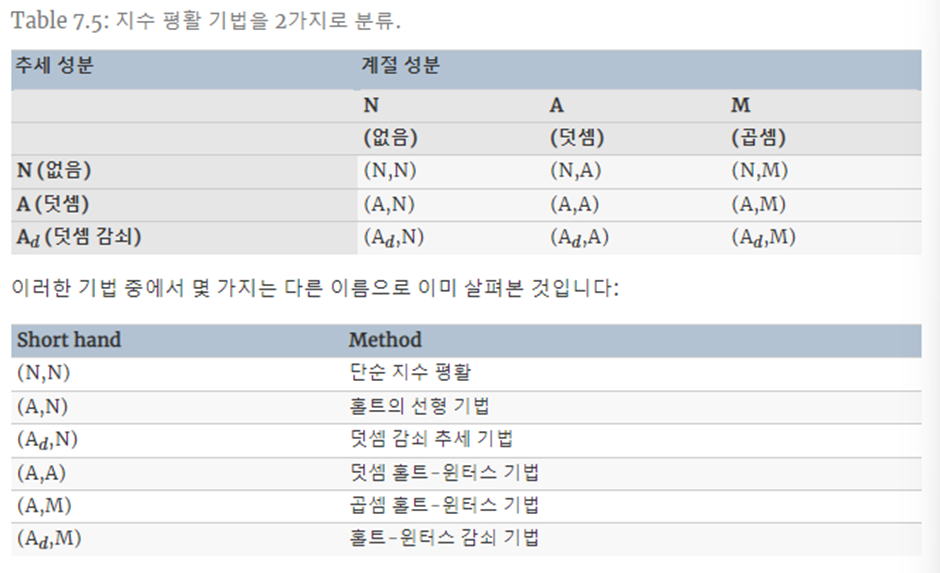
이 9가지 지수 평활기법에 대한 평활식 table이다

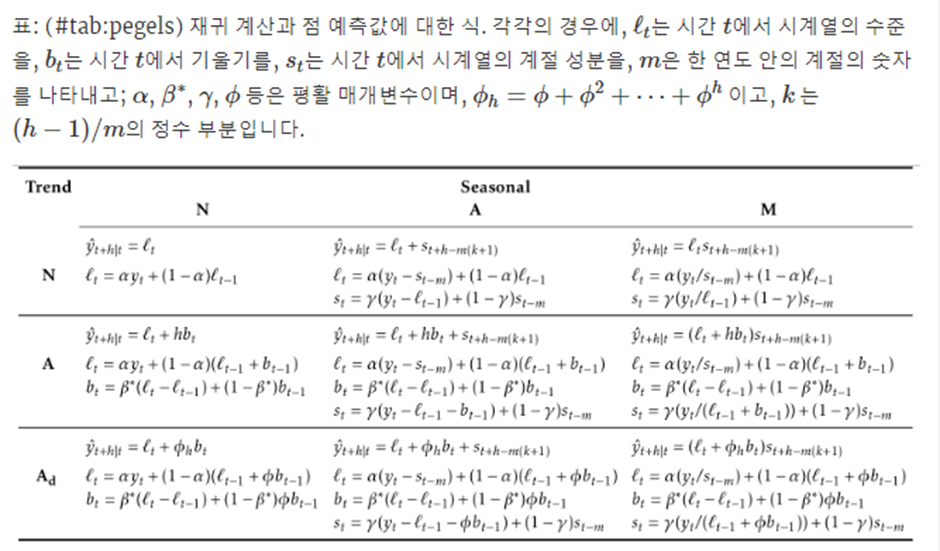
예측의 과정
1. Train Set과 Test Set을 분리한다 시계열 데이터에서는 가장 최근 기간을 Test Set으로 잡는다( 여기서 Test Set은 최소 우리가 실제로 예측하고 싶은 기간만큼의 길이는 되어야 한다)
2. 모델에 Train Set을 fitting 하고나서 Test Set 기간에 해당되는 기간을 예측한다
3. 이 예측값과 실제 Test Set Value를 비교하면서 모델을 평가하고 refit 과정을 거치면서 모델을 도출한다
4. 모델 선정후 전체 Train Set에 대해 학습을 한번 더 한다
5. 이후 예측하고 싶은 기간을 예측한다

3. ETS모델

가. ETS모델과 상태 공간 모델

• 상태 공간 모델은 위에서 지수평활기법에 깔린 통계적인 모델이다
  
• 우리는 각 관측값이 있고 이 관측값을 이용해서 예측을 수행할 수 있음을 앞에서 보았다
  여기서는 그렇게 만들어낸 예측과 실제 관측값 사이에 우리는 오차를 정의하게 되는데 이 오차의 분포를 정의 함으로써 예측값의 분포를 정의할 수 있다
• 혁신 상태 공간 모델은 관측된 데이터를 묘사하는 측정방정식(measurement equation)과 관측되지 않은 성분이나 상태(수준,추세,계절성)가 시간에 따라 어떻게 변하는지 기술하는 몇가지 상태방정식(state equation)으로 구성됐다

측정방정식은 은닉된 상태 변수가 관찰가능한 변수에 어떻게 영향을 미치는지 설명한다

상태방정식은 은닉된 상태변수들의 고유한 변동을 설명한다( 상태공간 모델의 의미 )

• 여기서는 AIC, AICc, BIC등의 정보기준도 사용해서 모델을 객관적으로 선택할 수 있게 한다

ETS(A,N,N): 덧셈 오차를 이용하는 단순 지수평활
단순 지수평활의 성분식

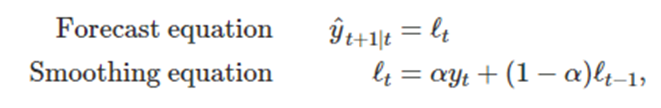
수준에 대한 평활식을 정리하면 오차 보정(error correction) 식을 얻는다

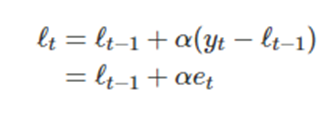
여기서 $e_t=y_t-l_{t-1}=y_t-{\hat{y}}_{t|t-1}$ 은 시간 t에서의 잔차(residual)이다
이런 잔차는 수준 평활식에서 오차보정의 역할을 하는데 예를들어 잔차가 음수라고 하자 그러면
예측값이 실제값보다 크다는 소리다 이 음수인 잔차를 수준에다 더해서 다음 수준에서는 좀 하향 조정 시킨다 수준 alpha가 1에 가까울수록 큰 조정이 일어나고 alpha가 작을수록 작은조정이 일어나 수준이 고르게 된다
관측값이 이전 수준에 오차를 더한 것과 같게 두기 위해 $y_t=l_{t-1}+e_t$ 라고 쓸 수 있다
우리는 이것을 혁신 상태 공간 모델(innovation state space model)로 만들기 위해(예측구간을 만드는 모델을 만들기 위해) $e_t$ 에 대한 확률 분포를 식으로 구체적으로 적는 작업이 필요하다. 이용하는 모델에 대해 잔차e_t가 평균이 0이면서 분산이 $sigma^2$인 정규분포를 따르는 백색잡음이라고 가정하자 이를 우리는
$e_t=\varepsilon_t$ ~ $NID{\left(0,\sigma^2\right)}$ 라고 쓴다 여기서 NID는 정규적으로 그리고 독립적으로 분포된(normally and independently distributed)라는 말을 줄여 쓴 것이다

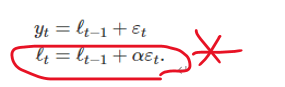
첫번째 식은 측정식(관측식)이고 두번째식은 상태식이다
오차의 통계적인 분포를 함께 이용한 이러한 두 식이 전체적으로 명확한 통계 모델을 이룬다
이러한 식이 단순 지수 평활을 이루는 혁신 상태 공간 모델이 된다 혁신이라는 단어는
모든 식이 무작위 오차 과정 $\varepsilon_t$을 사용한다는 사실에서 유래한다
우리는 *을 "t+1에 대한 예측이 결국 t에대한 예측 +확률변수 오차를 더한것"으로 볼 수 있다 이때 오차는 분포를 갖고 있으므로 우리는 예측에 대한 예측구간을 작성할 수 있게 되는 것이다

ETS(M,N,N); 곱셈 오차를 사용하는 단순 지수 평활
한 단계앞 학습 오차를 상대적인 오차로 기술하여 곱셈 오차를 고려하는 모델을 세울 수 있다

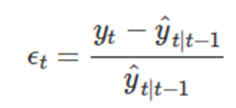
여기서 $\varepsilon_t$ ~ $NID(0,sigma^2)$ 이다 따라서 위식을 정리하면 분자가 $e_t$임을 감안할떄
$e_t = l_{t-1}*\varepsilon_t$라고 쓸 수 있다
그러면 상태공간의 곱셈 형태를 다음과 같이 쓸 수 있다

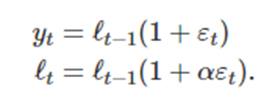
우리는 위에서 배운 9가지 지수평활 모델에 오차를 추가해서 혁신 상태 공간 모델을 쓸 수 있다

Holt-Winters Seasonality method와 ETS method의 차이점이 궁금할 수 있다
나름대로 생각한 차이점을 기술해 보자면 홀트 윈터스의 계절성 기법은 현재의 관찰값으로 기반한 현재 상태에 대한 예측과 이전 시점에 대해서 추정한 상태값의 가중 평균을 내서 현재 상태를 구한후 이를 기반으로 다음시점을 예측한다
ETS 모델은 현재시점에 대한 예측 분포$\varepsilon$-(평균은 0, 분산은 $\sigma^2$)를 갖는 오차 (현재시점에서 예측값을 뺀값: 덧셈오차, 이를 예측값으로 다시 나눈 값: 곱셈오차) 를 분포로 정의 함으로써 현재시점의 상태에 대한 분포를 기반으로 현재값에 대한($y_t$) 분포를 만들어 낸다

나. 가능도와 모델선택

예를 들어보자 우리는 평균 몸무게가 4kg이고 표준편차가 0.5인 고양이 몸무게에 대한 정규분포를 갖고있다 하지만 우리집 고양이는 5kg이다 이때 Likelihood는 무엇일까?
-> X = 5일경우 확률분포의 Y절편이다

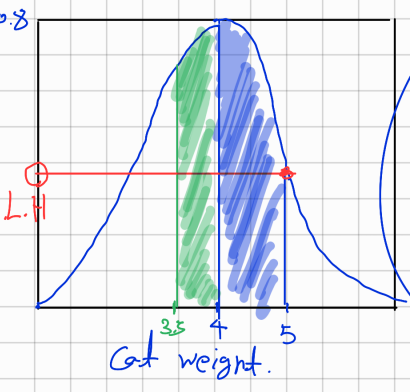
X=5 경우의 가능도는 이렇게 표현한다
L(N(4,0.5)|고양이 몸무게 = 5) = 0.108
여기서 만약 평균이5이고 표준편차가 0.5인 정규분포의 Likelihood가 고양이 몸무게가 5일 때 더 높다 즉, 고양이 몸무게가 5일 때 데이터를 더 잘 설명하는 분포는 N(5,0.5)이다 우리는 이렇게 어떤 파라미터를 포함하는 분포와 데이터가 있을 때 이 데이터들의 가능도를 측정해서 데이터를 더 잘 설명하는 분포를 찾아내는 것이다
따라서 다시 말하자면 가능도는 분포가 데이터를 얼마나 잘 설명하느냐 하는 척도이다
가능도를 수학적으로 표현하면 다음과 같이 표현한다

우리는 이 가능도를 이용해서 가능도를 최대로 하는 매개변수를 찾을 수 있다
우리는 또 여러 ETS모델중에 AIC AICc BIC등의 정보기준을 이용해서 제일 나은 모델을 찾을 수 있다

다. ETS모델로 예측하기

우리는 오차를 0(평균)으로 둬서 점 예측값을 얻음을 앞에서 봤다 이제 혁신 상태공간(ETS) 모델이 왜 앞에서 배운 평활 기법의 통계적인 모델인지 말해보겠다

ETS(M,A,N) 모델의 측정방정식을 보자

여기서 $\varepsilon_t=0$으로 둔다는 것은(오차가 없음) $y_t = \hat{y}_{t|t-1}$ 으로 두는 것이기 때문에 결국 t값에 대한 예측값은 $l_{t-1}+b_{t-1}$이 된다
비슷하게

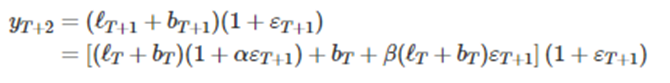
여기서 $\varepsilon_{t+1}=0$으로 두면

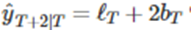
위와 같고, 이는 홀트의 선형 기법으로 얻은 예측값과 같다

ETS 점 예측값은 예측 분포의 중간값과 같다.
덧셈 성분만 이용하는 모델의 경우에는 예측 분포가 정규 분포라서 평균과 중앙값이 같지만
곱셈 오차를 이용하는 ETS모델이나 곱셈 계절성을 이용하는 경우에는 점 예측값은 예측분포의 평균값과 같지 않을 것 입니다.
이는 ETS 상태공간 모델의 측정식과 상태식을 보면 알 수 있다

예측구간
우리는 ETS 모델로 예측구간을 생성 할 수 있는데 대부분의 ETS 모델에 대해 예측구간은 다음과 같이 쓸 수 있다 , k는 포함확률(신뢰도)
$\sigma_h = 예측 표준편차$
[ 예측표준편차는 h가 커지면 커진다->불확실성이 커진다]