[알고리즘] 백 트래킹 문제 풀이

백준 2580

import java.io.*;
import java.util.*;

public class Main {
    static int[][] board;
    public static void main(String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        board = new int[9][9];

        for(int i = 0; i<9; i++){
            StringTokenizer st = new StringTokenizer(br.readLine());

            for(int j = 0; j<9; j++)
                board[i][j] = Integer.parseInt(st.nextToken());
        }

        sudoku(0, 0);
    }

    static void sudoku(int row, int col){
        if(col == 9){
            sudoku(row+1, 0);
            return;
        }

        if(row == 9){
            for(int i = 0; i<9; i++){
                for(int j = 0; j<9; j++)
                    System.out.print(board[i][j]+" ");
                System.out.println();
            }

            System.exit(0);
        }
        if(board[row][col] == 0){
            for(int i = 1; i<=9; i++){
                if(check(row, col, i)){
                    board[row][col] = i;
                    sudoku(row, col + 1);
                }
            }
            board[row][col] = 0;
            return;
        }

        sudoku(row, col+1);
    }

    static boolean check(int row, int col, int val){
        //가로 방향 탐색
        for(int i = 0; i<9; i++){
            if(board[row][i] == val)
                return false;
        }
        //세로 방향 탐색
        for(int i = 0; i<9; i++){
            if(board[i][col] == val)
                return false;
        }
        //3x3 박스 안 탐색
        int rowStart = (row/3)*3;
        int colStart = (col/3)*3;

        for(int i = rowStart; i<rowStart+3; i++){
            for(int j = colStart; j<colStart+3; j++)
                if(board[i][j] == val)
                    return false;
        }

        return true;
    }
}

얻어갈 점:

• 이전에 풀었던 NxN queen 문제와 비슷한 느낌이 들어 백 트래킹 알고리즘 채용
• 스도쿠를 풀어가며(dfs이용) 잘못 입력될 시 돌아오는 로직이기 때문
• 그러나 그때 NxN 문제에서는 초기화하고 돌아가는 로직이 없는데 같은 백트래킹이지만 구현이 다른 건가? 의문이 들어 둘 비교를 해봤음

---

vs 백준 9663

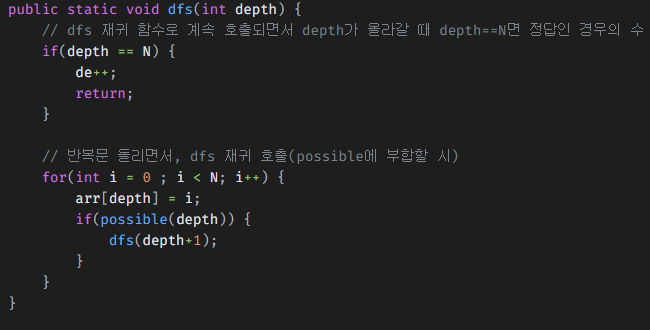
• 해당 문제 풀이 당시에는 for문을 돌리면서 arr[depth]에 값을 넣고 가능한 값이면 재귀호출 하는 구나~ 하며 풀이했음=> 즉, 모든 값이 불가능한 경우를 제외하고 로직을 구성(이전으로 돌아가는 것이 아닌 해당 depth의 값만 가능한 i값으로 바꾸면서 앞으로 쭉쭉 나가는 구나 생각)=> 그러나 잘 생각해보면 만약 for문을 다 돌았음에도 possible한 값이 없다면 for문 종료되고 이후 로직이 없으니 dfs 종료 => 호출이 종료되면 그 함수를 호출했던 부분 즉 dfs(depth+1)로 돌아감 => 남은 i값에 대한 for문 다시 호출해서 이전 값들이 수정되는 로직(우연히 맞은 문제였다는...)

---

다시 백준 2580 얻어갈 점?

• 스도쿠 문제의 경우 비어있는 경우 board[row][col] == 0 를 기준으로 탐색하기 때문에 9663문제와 다르게 값이 잘못되었다면 0으로 초기화해줄 필요가 있음(9663의 경우 잘못된 값을 초기화하지 않아도 arr[depth]==i를 넣어가며 값이 수정되어감)
• 따라서 board[row][col] = 0; return; 추가 => for문이 돌아가며 check를 통과하는 값이 없다면 해당 row,col==0으로 초기화해 다음에 또 다시 if 조건에 걸려 값을 넣어줄 것이고,return을 통해 재귀 호출했던 장소로 돌아감(만약 돌아간 곳도 또 값이 안되면 해당 row,col도 같은 로직 수행)
• 99 스도쿠에서 33으로 쪼개서 봐야하는 것을 구현하는 방식을 고민했는데 전체가 3칸으로 나뉘었으니 row,col 기준으로 0,1,2,3,4,5,6,7,8 => 0,1,2/3,4,5/6,7,8 => 이는 3으로 나누면 000/111/222 => 다시 3을 곱해주면 000/333/666으로 구현 가능