📒문제

📌풀이
import heapq
from collections import defaultdict
INF = int(1e9)
def solution(N, road, K):
def dijkstra(start):
distance = [INF for _ in range(N+1)]
q = []
heapq.heappush(q, [start, 0])
distance[start] = 0
while q:
now, dist = heapq.heappop(q)
if distance[now] < dist:
continue
for i in graph[now]:
cost = i[1] + dist
if cost < distance[i[0]]:
distance[i[0]] = cost
heapq.heappush(q, [i[0], cost])
return distance
graph = defaultdict(list)
result = []
for r in road:
graph[r[0]].append([r[1], r[2]])
graph[r[1]].append([r[0], r[2]])
result = dijkstra(1)
num = 0
for i in range(1, len(result)):
if result[i] <= K: num += 1
return num최소 힙을 이용한 최적화된 다익스트라 알고리즘을 사용하여 해결한 문제다. 이 문제를 보곤 특정 지점에서 모든 지점까지의 최소 거리를 구할 수 있는 다익스트라 알고리즘을 떠올렸다. 근데, 다익스트라는 매번 공부해도 막상 구현하려고 하면 잘 떠오르지 않는 것 같다. 그래서 오늘 이 문제를 계기로 좀 확실히 정리를 해두고 가려고 한다.
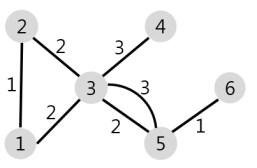
위의 그래프는 문제 예시 2에서 제시된 그래프를 구현한 것이다.
코드 설명
- 처음에는 distance[now]가 dist보다 작은지 확인해 주는데,
if distance[now] < dist: continue다익스트라는 최소 경로를 찾기 때문에 힙에는 최소 경로보다 돌아가는 경로 정보가 담길 수도 있다. 이때 여기서 now는 방문한 경로 노드, dist는 해당 경로로 지나갔을 때 시작점부터 경로노드까지의 임시 거리에 해당한다. 따라서 이 코드는 distance[now]와 dist를 서로 비교하여 distance[now]의 최소를 찾을 수 있게 돕는 코드이다.
(입출력 예 2에서 1->2->3 1->3같은 경우를 거르는 코드가 되겠다.)
for i in graph[now]: cost = i[1] + dist if cost < distance[i[0]]: distance[i[0]] = cost heapq.heappush(q, [i[0], cost])now 노드와 연결된 모든 노드에 대해 탐색을 진행한다. 여기서 dist는 now까지 이동하는데 걸린 거리, i[1]은 now노드에서 i[0]노드까지의 거리 를 의미 한다. 이때 우리가 알아야 할 것은 i[0]까지의 최소 거리이므로, distance[i[0]]에 저장된 값과 cost를 비교하여 최소로 값을 최신화 해주고, 해당 경로는 최소경로일 수 있으므로 최소경로 후보를 저장해놓은 최소 힙에 담는다.
👍 초기 상태)
1부터 출발하므로, (1, 0)을 heap에 담고, distance[1] = 0, 그 나머지를 INF로 초기화해준다.
힙의 상태 = [(1,0)]
distance= [0, INF, INF, INF, INF, INF ] (1부터 시작 가정)
👍 Step 1)
힙에서 (1, 0)을 꺼내준다. 1과 연결된 모든 노드에 대해서 탐색을 진행한다. 이때 1과 연결된 노드는 2와 3이다.
distance[2] = INF > 0(dist) + 1(i[1]) = 1
distance[3] = INF > 0(dist) + 2(i[1]) = 2 이므로 distance를 정리해주고, 힙에 담는다.
힙의 상태 = [(2, 1), (3, 2)]
distance= [0, 1, 2, INF, INF, INF ] (1부터 시작 가정)
👍 Step 2)
힙에서 (2, 1)을 뽑는다. 2와 연결된 모든 노드에 대해서 탐색을 진행한다. 2와 연결된 노드는 1과 3이다.
distance[1] = 0 < 1(dist) + 1(i[0]) = 2
distance[3] = 2 < 1(dist) + 2(i[0]) = 3 이므로, distance는 최신화할 필요가 없다. 따라서 그대로 종료한다.
힙의 상태 = [(3, 2)]
distance= [0, 1, 2, INF, INF, INF ] (1부터 시작 가정)
👍 Step 3)
힙에서 (3,2)를 뽑는다. 3과 연결된 노드에 대해서 탐색을 진행한다. 3과 연결된 노드는 4, 5 이다.
distance[4] = INF > 2(dist) + 3(i[0]) = 5
distance[5] = INF > 2(dist) + 2(i[0]) = 4
distance[5] = 4 < 2(dist) + 3(i[0]) = 5 이므로, distance를 최신화해주고 힙에 담는다.
힙의 상태 = [(5, 4), (4, 5)]
distance= [0, 1, 2, 5, 4, INF ] (1부터 시작 가정)
👍 Step 3)
힙에서 (5, 4)를 뽑는다. 5와 연결된 노드에 대해서 탐색을 진행한다. 5와 연결된 노드는 3, 6이다.
distance[3] = 2 < 2(dist) + 3(i[0]) = 5
distance[6] = INF > 4(dist) + 1(i[0]) = 5 이므로, distance를 최신화 해주고 힙에 담는다.
힙의 상태 = [(4, 5), (6, 5)]
distance= [0, 1, 2, 5, 4, 5 ] **
추후 힙에서 (4, 5)와 (6,5)를 뽑아도 달라지는건 없다. 따라서 해당 distance가 최종 결과가 된다.
