[알고리즘] 삽입 정렬과 병합 정렬

🎈 삽입 정렬

사진 출처

삽입 정렬은 한마디로 표현하면 정렬 범위를 1칸씩 확장해나가면서 새롭게 정렬 범위에 들어온 값을 기존 값들과 비교하여 알맞은 자리에 꼽아주는 알고리즘.

• 기준을 index=1로 잡고, key 왼쪽에 있는 수들은 이미 정렬이 된 것으로 가정하고 왼쪽에 있는 수들을 돌면서 key가 낑겨들어갈 알맞은 자리를 찾아주는 것이 알고리즘의 핵심

📢 시간/공간 복잡도

• 공간복잡도: 별도의 메모리 선언 없이 주어진 배열 내에서 정렬을 수행하므로 공간복잡도: O(1), in-place algorithm이라고 할 수 있다.
• 시간복잡도: 정렬할 값 key를 도는데 O(N)이 소요되고, key 왼쪽 정렬된 수를 돌면서 알맞은 자리를 찾는데 또 O(N)이 소요되므로 시간복잡도는 O(N^2)이라고 할 수 있다.
  (이미 정렬이 완료된 최선의 경우에는, key를 도는데 필요한 시간만 필요하므로 이때는 O(N))

📢 구현

def insertion_sort(arr):
	for end in range(1, len(arr)):
        key = arr[end]
        cur = end
        while cur > 0 and arr[cur - 1] > to_insert:
            arr[cur] = arr[cur - 1]
            cur -= 1
        arr[cur] = key
    
    return arr

---

🎈 병합 정렬

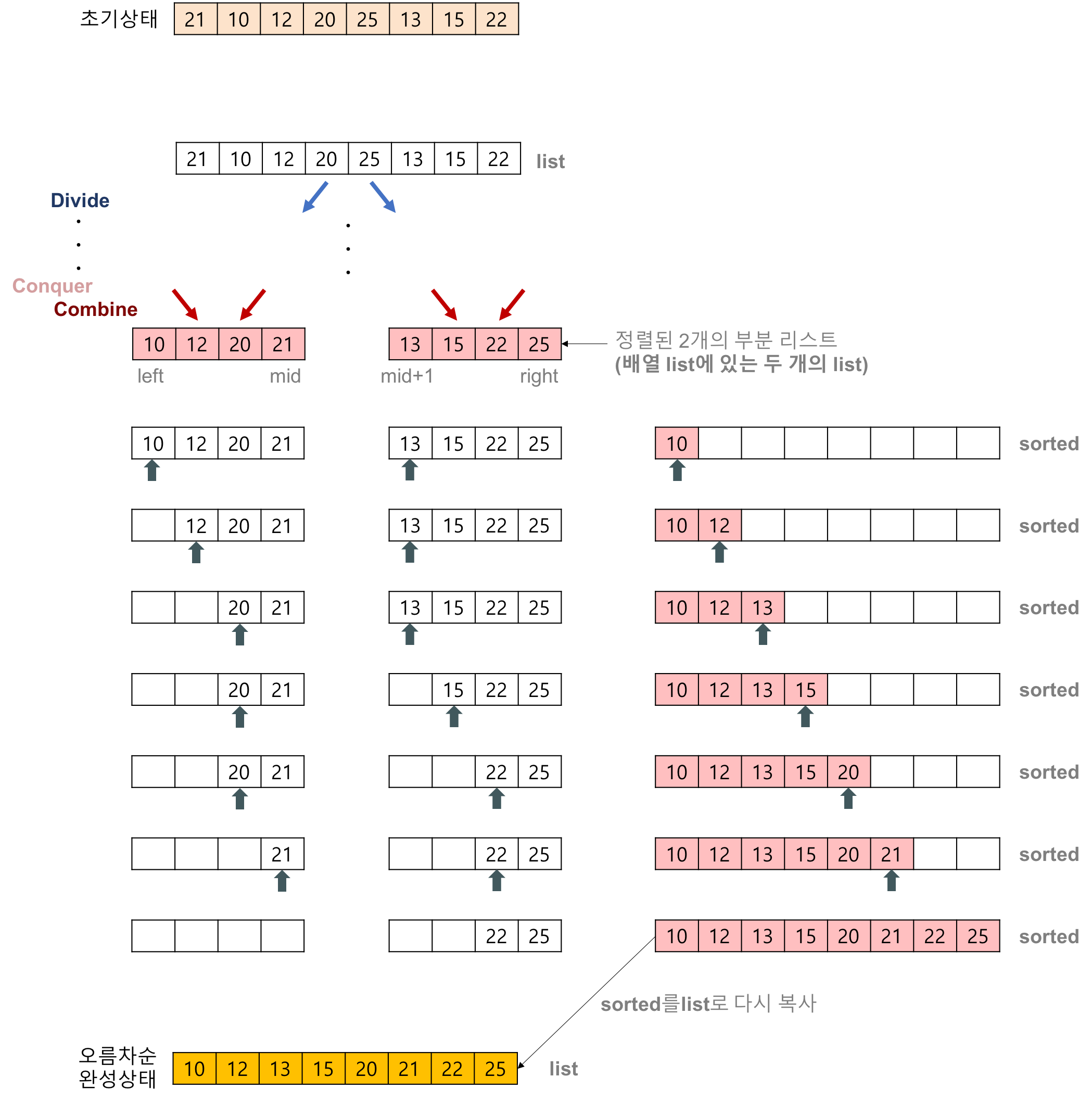
병합 정렬은 한마디로 표현하면 쪼갠 배열들을 정렬한 후 정렬한 작은 배열들을 다시 합쳐 새롭게 정렬된 배열을 생성하는 정렬 알고리즘

• 큰 문제를 작은 문제로 나누어 해결하기 때문에 divide and conquer 알고리즘이라 할 수 있다.

📢 시간/공간 복잡도

• 공간복잡도: 정렬할 결과를 담을 임시 배열 tmp가 필요하므로 O(N)
• 시간복잡도:
  1. N개의 요소로 이루어진 배열을 쪼개는데 필요한 단계 수는 O(logN)이다. (ex) 8개 배열을 절반으로 쪼개려면 총 log2(8) = 3)
  2. 이 쪼갠 배열들을 다시 하나로 합치는 데에는 O(N)이 필요하다.
  3. 따라서 병합 정렬의 O(NlogN)이라고 할 수 있다.

📢 구현

def merge_sort(arr):
    def sort(low, high):
        if high - low < 2:
            return

        mid = (low + high) // 2

        sort(low, mid)
        sort(mid, high)
        merge(low, mid, high)

    def merge(low, mid, high):
        tmp = []
        l, h = low, mid

        while l < mid and h < high:
            if arr[l] <= arr[h]:
                tmp.append(arr[l])
                l += 1
            else:
                tmp.append(arr[h])
                h += 1

        while l < mid:
            tmp.append(arr[l])
            l += 1

        while h < high:
            tmp.append(arr[h])
            h += 1

        for i in range(low, high):
            arr[i] = tmp[i-low]

    sort(0, len(arr))

    return arr