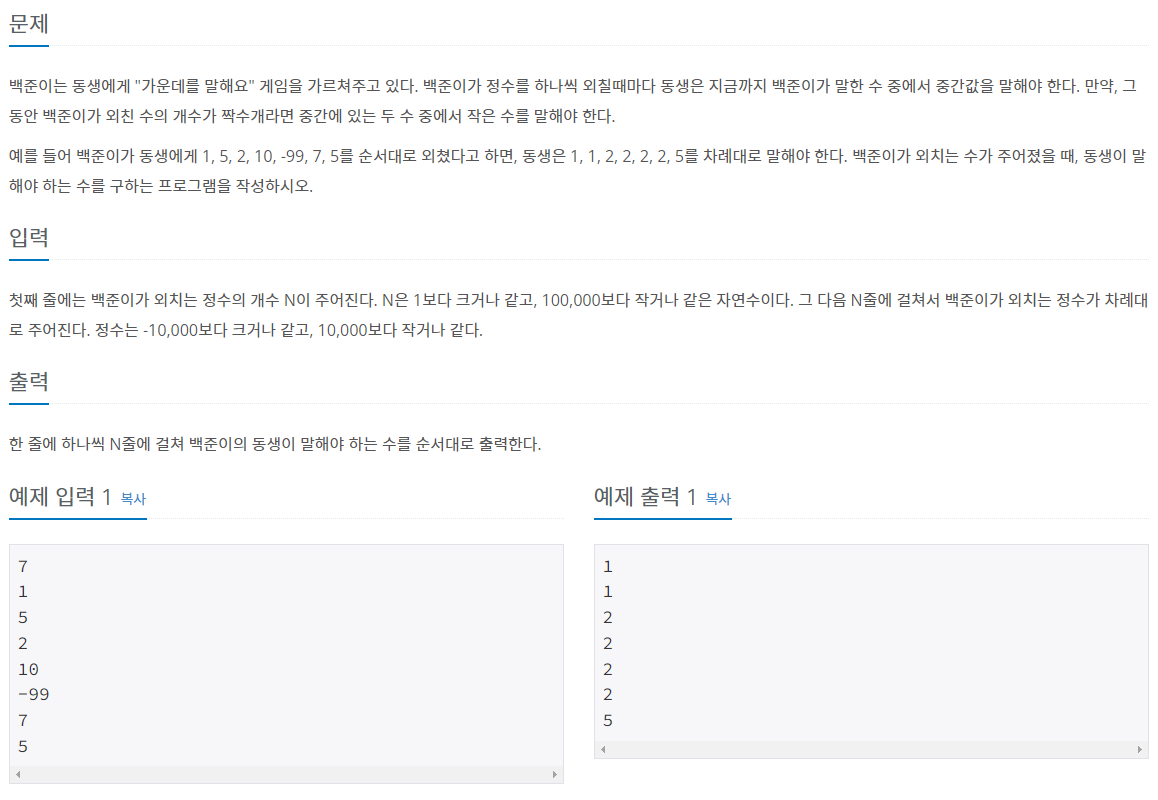
📒문제
📢풀이
N의 범위가 1부터 100,000이하이고, 시간 제한이 0.6초로 제한된 이상 이 문제는 input을 받을 때마다 정렬해서 중간값을 내는 방식으로는 문제의 시간 제한을 통과 할 수 없다. 따라서 다른 방법이 필요하다.
이 문제는 최소 힙과 최대 힙을 이용한 우선순위 큐(Priority Queue)를 이용하여 푸는 문제였다.
문제의 핵심 아이디어는, 수열을 각각 A 집합과 B 집합으로 나눌 때 A 집합에 있는 수가 B 집합에 있는 모든 수보다 작다고 가정한다면, 중간값에 해당하는 값은 A집합에서 가장 큰 수이고 B집합에선 가장 작은 수가 된다는 것이다. 따라서 최소 힙과 최대 힙을 이용하여 문제를 해결 할 수 있다.
import heapq
N = int(input())
l_heap = [] #최대 힙
r_heap = [] #최소 힙
answer = []
for i in range(N):
t = int(input())
if len(l_heap) == len(r_heap):
heapq.heappush(l_heap, -t)
else:
heapq.heappush(r_heap, t)
if r_heap and -l_heap[0] > r_heap[0]:
tmp_1 = heapq.heappop(l_heap)
tmp_2 = heapq.heappop(r_heap)
heapq.heappush(l_heap, -tmp_2)
heapq.heappush(r_heap, -tmp_1)
answer.append(-l_heap[0])
for i in answer:
print(i)풀이 해설
중간값보다 작은 값을 저장해두는 힙을 l_heap으로 두고, 최대값을 뽑을 수 있도록 최대 힙으로 이용한다. 중간값보다 큰 값을 저장해두는 힙을 r_heap으로 두고, 최소값을 뽑을 수 있도록 최소 힙을 이용한다.
이때, 문제의 조건에서 배열의 길이가 짝수일 때 중간 값은 더 작은 값으로 설정한다고 했으므로, 값을 두는 우선순위는 l_heap이 우선이어야 한다. 따라서 l_heap과 r_heap의 길이가 같을 때는 l_heap에 먼저 값을 넣고, r_heap에 나중에 값을 넣어주게 되는 것이다.
if len(l_heap) == len(r_heap):
heapq.heappush(l_heap, -t)
else:
heapq.heappush(r_heap, t)이때, 길이가 같을 때 l_heap에 넣은 값이 r_heap의 최솟값보다 큰 경우가 발생 할 수 있다. 이는 곧, 현재 넣은 값이 중간값보다 크다라는 것을 의미하므로, l_heap의 최대값(지금 방금 넣은 값)과 r_heap의 최솟값을 서로 swap해주어야 한다.
if r_heap and -l_heap[0] > r_heap[0]:
tmp_1 = heapq.heappop(l_heap)
tmp_2 = heapq.heappop(r_heap)
heapq.heappush(l_heap, -tmp_2)
heapq.heappush(r_heap, -tmp_1)📢느낀 점
힙까지는 생각을 못해본 건 아닌데 이렇게 힙을 최소 힙과 최대 힙으로 나눠서 중간값을 구하는 방법은 생각도 못한 방법이었다. 힙의 원리를 중간값의 특징과 연관지어 생각했다면 어렵지 않게 풀 수 있었을 문제인 것 같다.
