[백준 12865, Gold V] - 평범한 가방

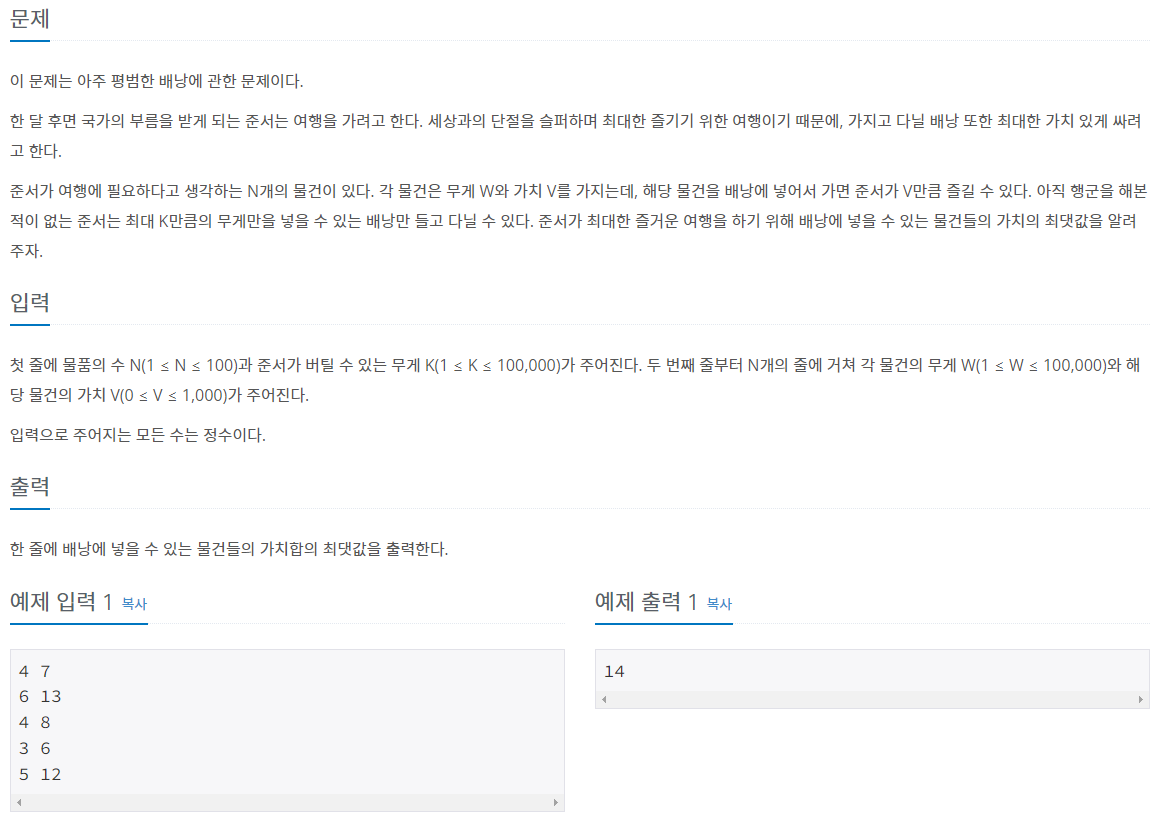
📒문제

---

🎈풀이

이 문제는 dp로 풀 수 있는 전형적인 0-1 Knapsack 문제였다.

Knapsack 문제는?
배낭에 담을 수 있는 무게의 최대값이 정해져 있을 때, 최대의 가격 합을 가지면서 배낭에 담을 수 있도록 하는 경우를 찾도록 하는 알고리즘이다.

이 문제는
1) Brute Force 방식으로 이론상 풀 수는 있지만, 시간복잡도가 어마어마하게 오래 걸린다. (무려 O(2^N))
2) Greedy 한 방식으로는 풀 수 없다. (반례 발생)

따라서 이 문제는 큰 문제를 작은 문제로 쪼개서 푸는 DP의 기법을 사용해야 한다.

📢 DP 최적의 원리) 어떤 문제를 DP로 풀 수 있으려면 최적의 원리가 성립해야 한다.
어떤 문제의 입력사례의 최적해가 그 입력사례를 분할한 부분사례에 대한 최적해를 항상 포함할 시에는 최적의 원리가 성립한다.

이 문제에 최적의 원리를 적용해 본다면,

이 문제의 최적해 집합(n개의 물건중 가장 최적으로 물건을 고른 부분집합)을 A라고 가정하자.

• 만일 A가 x번째 보석을 포함하지 않는다면, A는 x번째 보석을 제외한 나머지 x-1개의 보석들 중에 최적으로 고른 부분집합과 같다.
• 만일 A가 x번쨰 보석을 포함한다면, A는 x-1개의 보석들 중에 최적으로 고른 부분집합에서 x번째 보석을 추가한 부분집합과 같다.

사진 출처 1

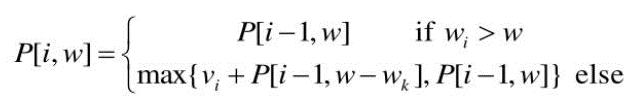
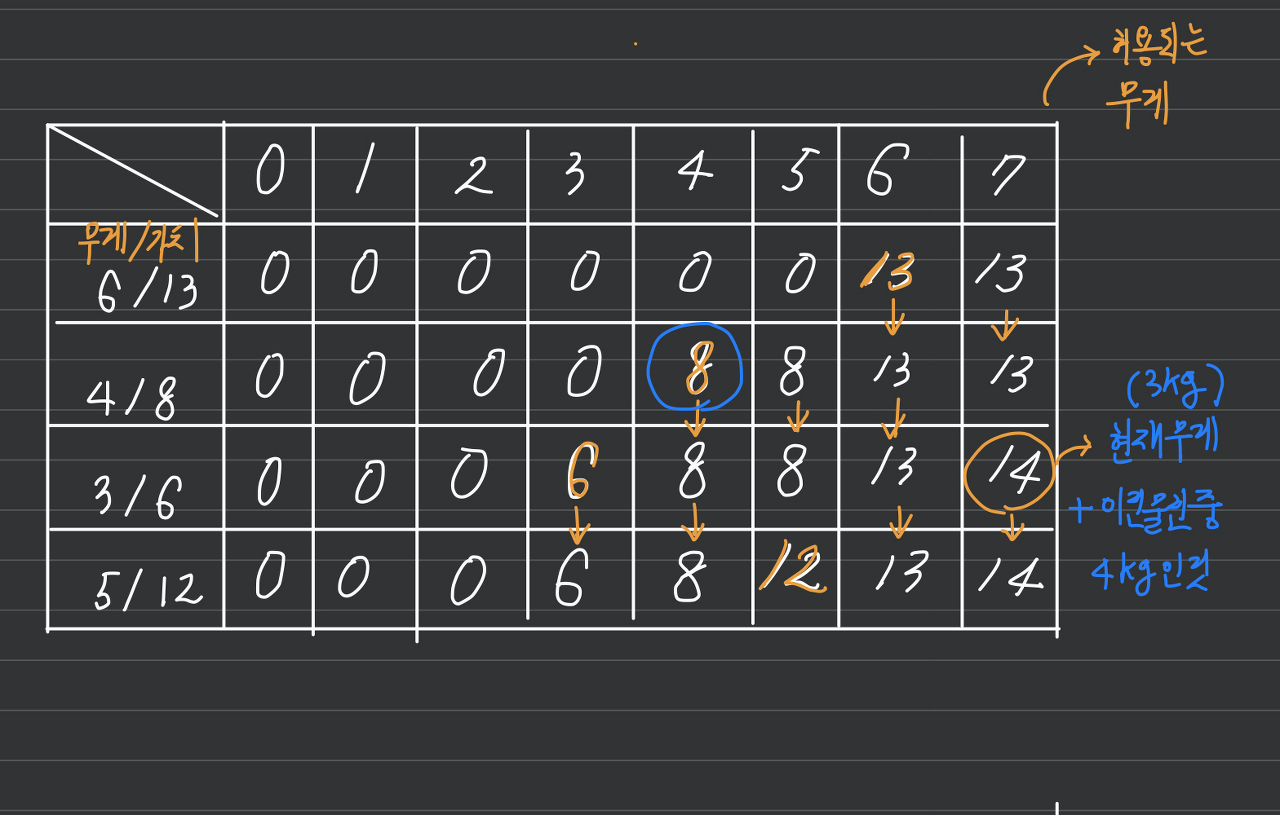
따라서 위와 같은 점화식을 세울 수 있는데,(이때 i = 보석 수, w = 무게 한도) 이 말인 즉슨,

• i번째 보석이 배낭 무게 한도보다 무거우면 배낭에 넣을 수 없으니, i-1번째 보석들을 가지고 만든 최적 집합을 그대로 가지고 온다.
• 그렇지 않다면, i번째 보석이 들어갈 수 있도록 무게를 비운 최적집합에 i번째 보석을 추가한 값과 i-1번째 보석까지의 최적 집합 중 더 최적화된 집합을 선택한다.

사진 출처 2

def solution(N, K, things):
    result = -1
    dp = [[0 for _ in range(K+1)] for _ in range(N+1)]

    things.insert(0, (0, 0))


    for i in range(1, N+1): # i = 물건 번호
        weight, value = things[i][0], things[i][1]
        for j in range(1, K+1): # j = 담을 수 있는 무게 최대
           
            if weight <= j:
                dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight] + value)
            else:
                dp[i][j] = dp[i-1][j]
            
            result = max(result, dp[i][j])
            
    return result

N, K = map(int, input().split())
things = []
for _ in range(N):
    things.append(tuple(map(int, input().split())))

print(solution(N, K, things))

문제 자체의 구현은 빠르게 이해한 편인 것 같은데, 배열 인덱스가 너무 헷갈렸다. (K+1인지, N+1인지....) 많이 풀다 보면 이런것도 없어지겠지...?