[프로그래밍언어] - Top-down parser

📜 Top-down Parser

👍 개요

📢 정의

• LL = Left-to-right input scan, Leftmost Derivation
• Parse tree의 root부터 시작해서 가지와 잎을 그리는 파싱 방식
• Production rule을 하나 선택하고, 파싱 되도록 input을 끼워맞춘다!

📢 Top-down parsing의 문제점

• 만일 잘못된 production rule을 택했다면, backtracking을 해야한다.
  • 하지만 backtracking을 하지 않는, predictive parsing을 할 수 있는 LL(1) 특성을 갖는 문법이 존재한다.
  • LL(1) 특성을 갖지 않는 문법이라도 Left-factoring을 할 수 있는 문법이라면 LL(1) 특성을 갖게 할 수도 있다!
• Left-Recursion이 발생하게 되면 Infinite loop에 빠지는 문제가 발생한다.

👍 Left-Recursion

📢 Left Recursion이란?

• 쉽게 풀어쓰면, 만약 A가 non-terminal에 속하고, A가 Aa(이때 a는 terminal일수도, non-terminal일수도 있음)로 derive 가능할 때 이 grammar는 left-recursive 하다.
• Left-recursion은 top-down parsing이 infinite loop에 빠지게 하는 원인이 될 수 있다. => right- recursion으로 바꿔 쓰자!

📢 Solution: Left-recursion을 바꿔쓰자!

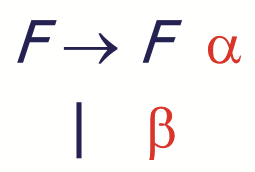
• 현재 이 grammar는 left-recursive한 grammar이다. (Non-terminal F가 왼쪽에 재등장 하기 때문)
  
• 이거와 같이 바꿔쓴다. (새로운 non-terminal P를 추가하였고, 입실론이 production rule에 추가된다.)
• 위의 예시는 left-recursion의 특성 대신 right recursion의 특징을 갖도록 했으며, left-associativity(같은 우선순위에 있다면 왼쪽부터 묶어서 해석)은 유지된다.

👍 Predictive Parsing

• 기본 아이디어는 non-terminal A가 alpha 또는 beta로 derive 가능할 경우, parser가 고민없이 alpha 혹은 beta를 선택할 수 있도록 하는것!

📜 기본 아이디어 - First set

• 모든 symbol alpha에 대해서, First(alpha)는 derive시 첫 번째로 나타나는 symbol(terminal)들의 집합이다.

📢 Building First set
Symbol X에 대한 First set을 구한다고 가정해보자.

• X가 terminal일때, First(X) = {X}이다.
• X가 epsilon으로 deriving 될 때, epsilon은 First(X)에 포함된다.
  
• X가 가 y1y2....yk로 derive 될 수 있을 때,
  1. 만일 epsilon이 First(X)에 포함된다면, First(y1), First(y2)...First(yk)는 모두 epsilon을 포함해야 한다.
  2. 만일 terminal a가 First(X)에 포함될 때, First(yi)=a라면, 1<=h<i에 대해 모든 First(yh)는 epsilon을 포함해야한다.
  3. 만일 First(yi)가 epsilon을 포함하지 않는다면, k>i에 대해서 First(yk)를 탐색하는 것은 무의미하다.

📜 기본 아이디어 2 - Follow set

• Non-terminal symbol alpha에 대해서, FOLLOW(alpha)는 derive시 alpha뒤에 나타나는 모든 terminal들의 집합이다.

📢 Building FOLLOW set
Symbol X에 대한 Follow set을 구한다고 가정해보자.

• X가 Starting non terminal이라면, EOF를 FOLLOW(X)에 추가해준다.
• A → αB, A → αBβ 에서,
  1. A → αB에서, FOLLOW(B)에 FOLLOW(A)를 추가한다. -> 반대가 맞는거 아닌가?
  2. 만일 β가 terminal이라면 FOLLOW(B)에 β를 추가한다.
  3. 만일 β가 non-terminal이라면, FOLLOW(B)에 First(β)-e를 추가한다.
  4. 만일 First(β)에 e가 포함된다면, FOLLOW(B)에 FOLLOW(A)를 추가한다.

📢 Building FOLLOW set 다시 정리하기
1. 모든 FOLLOW set에는 EOF가 포함된다.
2. FOLLOW를 구하려는 non-terminal 뒤에 terminal이 있다면 그 terminal을 FOLLOW에 포함시킨다.
3. 구하려는 non-terminal뒤에 아무것도 오지 않는다면 구하려는 non-terminal의 좌변 non-terminal의 FOLLOW를 찾아 넣는다.
4. 구하려는 Non Terminal 다음에 Non Terminal이 나온다면이 Non Terminal의 First를 구하면된다. 만약 다음 Non Terminal의 First가 이라면 이 3번 규칙을 다시 적용하면 된다
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=noma000&logNo=220902314630 -> 연습하기...

👍 Left-factoring

• 찾을 수 있는 가장 긴 prefix α에 대해, 새로운 Non-terminal Z를 추가한 후 위와 같이 문법을 바꿔 쓸 수 있다.

📜 LL조건

• LL조건을 만족하는 Predictive parsing이 가능한 문법이려면, 다음과 같은 두가지 조건을 만족해야 한다.

  임의의 production rule A → α | β에 대해서,

  • First(α)와 First(β)의 교집합은 공집합이어야 한다.
  • First(α)에 e가 포함된다면, Follow(α)와 First(β)의 교집합은 공집합이어야 한다.

• LL조건을 판단하려면, 문법이 Left-recursive하진 않은지, Left-factoring을 제거하고 판단해야 한다. => Left-recursive와 Left-factoring의 요소를 전부 제거했다고 해서 그 문법이 LL(1)을 꼭 만족한다고 말할 수는 없다!

뒤에 Automative predictive parser 부분은 좀 물어보고 나중에 다시 정리하기....