https://programmers.co.kr/learn/courses/30/lessons/72412

---

1. 전체 코드

from bisect import bisect_left, bisect_right
from itertools import combinations
from collections import defaultdict
import heapq

import re
def solution(info, query):
    answer = []
    member = []
    q = []
    d = defaultdict(list)

    for j in info:
        a = j.split()
        member.append(a) ## a = ['java', 'backend', 'junior', 'pizza', '150']
        

    for j in query:
        s = re.sub('and', '', j)
        s = s.split() 
        q.append(s)  ## s = ['-', '-', '-', 'chicken', '100']
	
    a = [0, 1, 2, 3]
    for k in member:
        temp = []
        # '-' 없는 검색 -> 1개
        temp.append(k[:4])

        # '-' 1개 -> 4C1 -> 4개
        temp.append(['-', k[1], k[2], k[3]])
        temp.append([k[0], '-', k[2], k[3]])
        temp.append([k[0], k[1], '-', k[3]])
        temp.append([k[0], k[1], k[2], '-'])

        # '-' 2개 -> 4C2 -> 6개
        arr_two = list(map(list, combinations(a, 2)))
        for j in arr_two:
            temp_k = k[:4]
            x, y = j
            temp_k[x] = '-'
            temp_k[y] = '-'
            temp.append(temp_k[:])

        # '-' 3개 -> 4C3 -> 4개
        arr_three = list(map(list, combinations(a, 3)))
        for j in arr_three:
            temp_k = k[:4]
            x, y, z = j
            temp_k[x] = '-'
            temp_k[y] = '-'
            temp_k[z] = '-'
            temp.append(temp_k[:])

        # '-' 4개 -> 1개
        temp.append(['-', '-', '-', '-'])
        
        for j in temp:
            d[''.join(j)].append(int(k[4]))
            
    # 풀이-4번 설명
    for key in d.keys():
        d[key].sort()
    
    # 효율성 X -> 풀이-3번 설명
    # for j in q:
    #   d[''.join(j[:4])].sort()

    for j in q:
        a = d[''.join(j[:4])]
        left = bisect_left(a, int(j[4]))
        right = bisect_right(a, 100000)
        answer.append(right - left)
    return answer

---

2. 후기 및 설명

1. 시간복잡도 O(N*M)의 풀이로 풀게 된다면, O(50,000 * 100,000) = O(5,000,000,000)의 시간복잡도가 소요된다. 체점용 서버는 파이썬이 1초에 약 20,000,000번 정도의 연산만 처리할 수 있다고 가정하고 문제를 풀어야하기 때문에, 이 풀이의 경우 25초의 시간이 소요된다. 이 문제의 정답률이 낮았던 이유는 효율성 테스트를 통과하기 매우 까다롭기 때문이다.

2. member 배열에 담긴 k = ['java', 'backend', 'junior', 'pizza', '150']가 어떠한 query(=q)들로 검색될 수 있을지 생각해야 한다. '-'를 생각한다면 각각의 k는 아래의 16가지 형식의 그룹으로 묶을 수 있다. 자세한 설명은 해설 참고

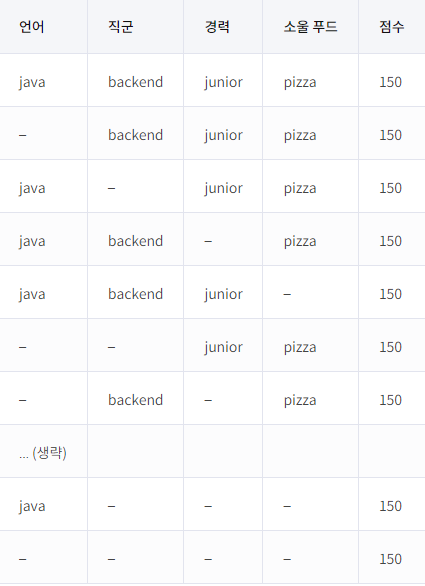
3. 처음에는 q(=query)에 해당하는 d[''.join(j[:4])]의 값만 정렬 하는게 효율적이라 생각했지만, 효율성 테스트를 통과하지 못했다. 예제와 다르게도 q는 최대 100,000개의 값을 가질 수 있고 sort()는 O(nlogn)의 시간복잡도를 가지기 때문에 각 그룹에 묶인 점수들d[key] =[150, 200, 80 .....]의 길이 n이 클 경우 시간초과가 발생할 수 있다고 생각했다. 또한 동일한 d[key]에 대해 중복된 sort()가 수행되는 것도 생각할 수 있다.

4. 사전형 d의 길이는 모든query 조합을 고려한다 해도 기껏해야 수백, 수천가지의 그룹이 한계일 것이다. 따라서 for문을 통한 동일한 sort() 수행 시 시간복잡도 측면에서 훨씬 유리하다.