[CS] 알고리즘 시간복잡도 정리 (Big-O, Big-Ω, Big-θ)

Hyunjun Kim·2025년 5월 7일

Algorithms CS 알고리즘

Computer_Science

목록 보기

4/19

1. 알고리즘 복잡도란?

알고리즘의 성능을 정량적으로 비교할 수 있는 지표로 시간복잡도와 공간복잡도가 있다.

시간복잡도(Time Complexity): 입력 크기 N이 증가할 때 연산 횟수가 얼마나 증가하는지를 나타낸다.

공간복잡도(Space Complexity): 입력 크기 N이 증가할 때 필요한 메모리(공간) 가 얼마나 증가하는지를 나타낸다.

2. 시간복잡도 표기법의 종류

Big-O Notation, Big-Omega Notation, Big-Theta Notation

표기법	의미	설명
Big-O	최악(Worst case)	입력값 중 가장 많은 시간 소요 상황을 기준. 가장 일반적, 보수적 평가.
Big-Ω	최선(Best case)	가장 빠르게 동작하는 최상의 입력에 대한 시간
Big-θ	평균(Average case)	평균적인 입력에 대한 실행 시간 (엄밀한 수학적 분석 필요)

실무 및 알고리즘 문제에서는 대부분 Big-O 기준으로 성능을 판단한다.

3. Big-O 표기법의 핵심 규칙

복잡도 표기에서 실제 시간 측정보다는 성장률(Growth rate) 이 중요하다.

상수항 제거: O(N + 5) → O(N)
계수 제거: O(3N) → O(N)
최고차항만 사용: O(3N³ + 2N² + N + 5) → O(N³)

즉, 입력이 커질수록 영향력이 미미한 요소(상수, 낮은 차수) 는 무시한다.

4. 자주 사용하는 시간복잡도 종류와 예시

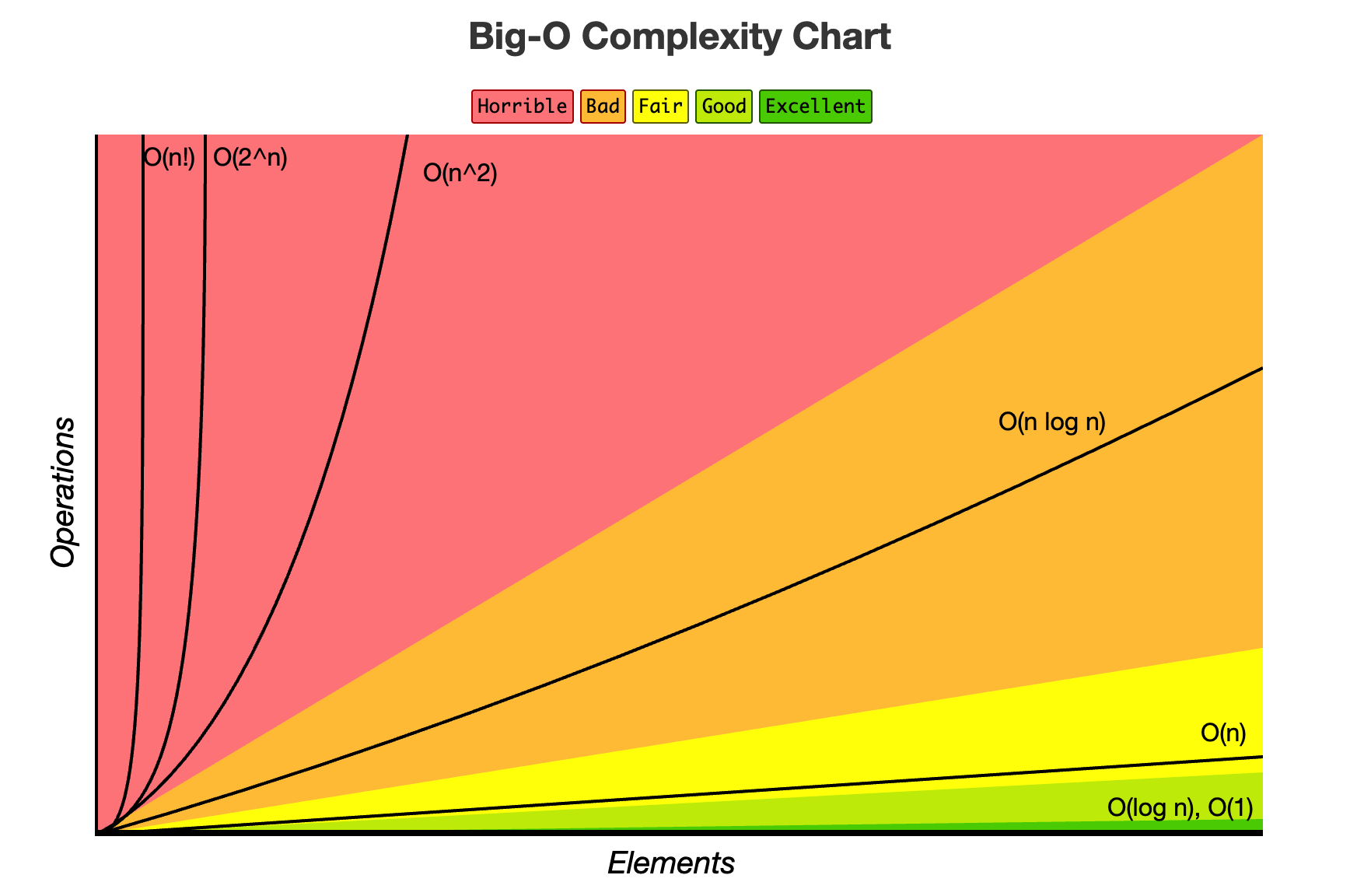
이미지 출처 : https://www.bigocheatsheet.com/

시간복잡도	영어 표기	한글 의미	예시 알고리즘 또는 연산
O(1)	Constant Time	상수 시간	배열 인덱스 접근, 스택 `push/pop`, 딕셔너리 `get`
O(log N)	Logarithmic Time	로그 시간	이진 탐색, 힙 삽입/삭제
O(N)	Linear Time	선형 시간	단일 for문 순회, 배열 전체 합산
O(N log N)	Linearithmic Time	선형로그 시간	병합 정렬, 퀵 정렬 평균, 힙 정렬
O(N²)	Quadratic Time	이차 시간	2중 for문, 버블 정렬, 삽입 정렬
O(N³)	Cubic Time	삼차 시간	3중 for문, 플로이드-워셜 알고리즘
O(2ⁿ)	Exponential Time	지수 시간	피보나치(재귀), 조합 문제 전체 탐색
O(N!)	Factorial Time	팩토리얼 시간	순열 생성, 외판원 문제(브루트포스)

5. 코드 예시로 이해하는 시간복잡도

# O(1)
def get_first_element(arr):
    return arr[0]

# O(n)
def sum_elements(arr):
    total = 0
    for x in arr:
        total += x
    return total

# O(n^2)
def all_pairs(arr):
    for i in arr:
        for j in arr:
            print(i, j)

# O(log n)
def binary_search(arr, target):
    left, right = 0, len(arr)-1
    while left <= right:
        mid = (left + right) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return -1

6. 시간복잡도 판단 팁

6.1. 입력 범위별 시간 제한 기준

입력 크기(N)	시간 복잡도 허용 범위
`N ≤ 10`	`O(N!)`, `O(2^N)` 가능
`N ≤ 100`	`O(N^3)` 이하 가능
`N ≤ 1,000`	`O(N^2)` 이하 가능
`N ≤ 100,000`	`O(N log N)` 이하 권장
`N ≤ 1,000,000`	`O(N)` 이하 권장