선형모델_Linear Regression

maro·2024년 5월 17일

머신러닝

선형회귀 개요

선형 회귀(線型回歸, Linear regression)는 종속 변수 y와 한 개 이상의 독립 변수X와의 선형 상관 관계를 모델링하는 회귀분석 기법. 위키백과

선형회귀 모델

각 Feature들에 가중치(Weight)를 곱하고 편향(bias)를 더해 예측 결과를 출력한다.
Weight와 bias가 학습 대상 Parameter가 된다.

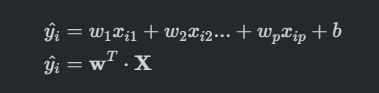
$\hat{y_i}$ : 예측값
$x$ : 특성(feature-컬럼)
$w$ : 가중치(weight), 회귀계수(regression coefficient). 특성이 $\hat{y_i}$ 에 얼마나 영향을 주는지 정도
$b$ : 절편
$p$ : p 번째 특성(feature)/p번째 가중치
$i$ : i번째 관측치(sample)

Boston DataSet

보스톤의 지역별 집값 데이터셋

CRIM : 지역별 범죄 발생률
ZN : 25,000 평방피트를 초과하는 거주지역의 비율
INDUS: 비상업지역 토지의 비율
CHAS : 찰스강에 대한 더미변수(강의 경계에 위치한 경우는 1, 아니면 0)
NOX : 일산화질소 농도
RM : 주택 1가구당 평균 방의 개수
AGE : 1940년 이전에 건축된 소유주택의 비율
DIS : 5개의 보스턴 고용센터까지의 접근성 지수
RAD : 고속도로까지의 접근성 지수
TAX : 10,000 달러 당 재산세율
PTRATIO : 지역별 교사 한명당 학생 비율
B : 지역의 흑인 거주 비율
LSTAT: 하위계층의 비율(%)
MEDV : Target. 지역의 주택가격 중앙값 (단위: $1,000)

Boston housing dataset loading

import pandas as pd
df = pd.read_csv("data/boston_hosing.csv")
df.shape

(506, 14)

X = df.drop(columns='MEDV')
y = df['MEDV']

# train/test set 분리
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

LinearRegression

가장 기본적인 선형 회귀 모델
각 Feauture에 가중합으로 Y값을 추론한다.
attribute(학습 후 조회가능)
- coef_: 각 Feature에 곱하는 가중치
- intercept_: y절편. 모든 Feature가 0일때 예측값

데이터 전처리

선형회귀 모델사용시 전처리
- 범주형 Feature
  - : 원핫 인코딩
- 연속형 Feature
  - Feature Scaling을 통해서 각 컬럼들의 값의 단위를 맞춰준다.
  - StandardScaler를 사용할 때 성능이 더 잘나오는 경향이 있다.

Feature scaling
## trainset으로 fit 한 것으로 train/test/validation set 변환.
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
모델 생성, 학습
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X_train_scaled, y_train)
#### 학습 후 찾은 weights 와 bias 조회
print("weights")
# print(lr.coef_)
pd.Series(lr.coef_, index=X.columns)
print("bias-모든 feature들이 0일 때 y값")
lr.intercept_
weights
CRIM -0.970820
ZN 1.057149
INDUS 0.038311
CHAS 0.594506
NOX -1.855148
RM 2.573219
AGE -0.087615
DIS -2.880943
RAD 2.112245
TAX -1.875331
PTRATIO -2.292767
B 0.718179
LSTAT -3.592455
dtype: float64
bias-모든 feature들이 0일 때 y값
22.611881188118804

Coeficient의 부호

weight가

양수: Feature가 1 증가할때 y(집값)도 weight만큼 증가한다.

음수: Feature가 1 증가할때 y(집값)도 weight만큼 감소한다.

절대값 기준으로 0에 가까울 수록 집값에 영향을 주지 않고 크면 클수록(0에서 멀어질 수록) 집값에 영향을 많이 주는 Feature 란 의미가 된다.

평가

## 회귀 - mse, rmse, (ma-절대값-e), r2
from metrics import print_regression_metrics
print_regression_metrics(y_train, lr.predict(X_train_scaled), title="Trainset")
print_regression_metrics(y_test, lr.predict(X_test_scaled), title="Testset")

Trainset
MSE: 19.326470203585725
RMSE: 4.396188144698282
R Squared: 0.7730135569264234
Testset
MSE: 33.448979997676496
RMSE: 5.783509315085133
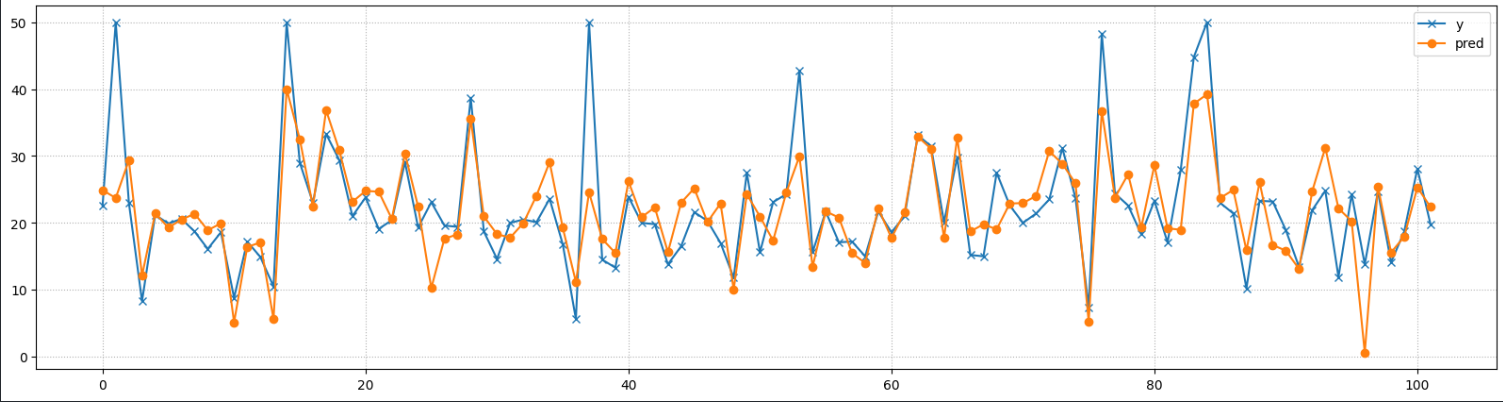
R Squared: 0.5892223849182512

####### Pipeline 이용
from sklearn.pipeline import Pipeline
pl = Pipeline([
    ("scaler", StandardScaler()), ("model", LinearRegression())
], verbose=True)
pl.fit(X_train, y_train)
pred = pl.predict(X_test)
pred[:10]

array([24.88963777, 23.72141085, 29.36499868, 12.12238621, 21.44382254,
19.2834443 , 20.49647539, 21.36099298, 18.8967118 , 19.9280658 ])

### y_test 정답과 추론값 비교 - 시각화
import matplotlib.pyplot as plt
plt.figure(figsize=(20, 5))
plt.plot(range(y_test.size), y_test, marker="x", label="y")
plt.plot(range(y_test.size), pred, marker='o', label="pred")
plt.legend()
plt.grid(True, linestyle=":")
plt.show()

다항회귀 (Polynomial Regression)

전처리방식 중 하나로 Feature가 너무 적어 y의 값들을 다 설명하지 못하여 underfitting이 된 경우 Feature를 늘려준다.
각 Feature들을 거듭제곱한 것과 Feature들 끼리 곱한 새로운 특성들을 추가한다.
- 파라미터(Coef, weight)를 기준으로는 일차식이 되어 선형모델이다. 그렇지만 input 기준으로는 N차식이 되어 비선형 데이터를 추론할 수 있는 모델이 된다.
PolynomialFeatures Transformer를 사용해서 변환한다.

예제

데이터셋 만들기

import numpy as np
np.random.seed(0)
# 모델링을 통해 찾아야 하는 함수.
def func(X):
    return X**2 + X + 2 + np.random.normal(0,1, size=(X.size, 1))
  # 노이즈를 추가. 평균이 0이고 표준 편차가 1인 정규분포 따름.
  # X와 같은 크기의 노이즈 배열을 생성.
  # 0.94978823 * X2 + 0.97906552 * X1 + 2.3405007562628866
m = 100
X = 6 * np.random.rand(m, 1) - 3
# -3에서 3 사이의 값을 가지는 100개의 샘플을 생성.
# 6 * np.random.rand(m, 1) - 3은 0에서 6 사이의 난수를 생성하고, 
# 이를 -3으로 평행 이동시켜 -3에서 3 사이의 값을 가지도록 함.
y = func(X)
y = y.flatten()
print(X.shape, y.shape)

(100, 1) (100,)

import matplotlib.pyplot as plt
plt.scatter(X,  y)
plt.show()

모델생성, 학습

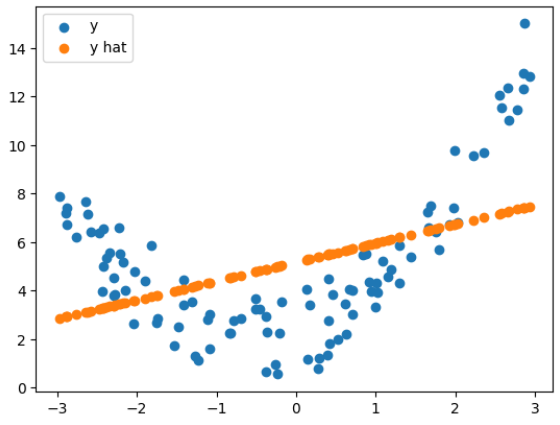
lr = LinearRegression()
lr.fit(X, y)
pred = lr.predict(X)

import matplotlib.pyplot as plt
plt.scatter(X,  y, label="y")
plt.scatter(X, pred, label='y hat')
plt.legend()
plt.show()

lr.coef_, lr.intercept_

(array([0.78189543]), 5.175619278567209)

print_regression_metrics(y, pred)

MSE: 7.729204760808937
RMSE: 2.7801447373848966
R Squared: 0.19138252437306003

PolynomialFeatures를 이용해 다항회귀구현

from sklearn.preprocessing import PolynomialFeatures
pnf = PolynomialFeatures(
	degree=2, # 최고차항의 차수. ex) 4로 지정. -> x(원래 컬럼), x^2, x^3, x^4  한 feature추가.
    include_bias=False # True(기본값) - 상수항 feature 생성여부. (모든 값이 1인 feature)
X_poly = pnf.fit_transform(X)
print(X.shape, X_poly.shape)

(100, 1) (100, 2)

LinearRegression 모델을 이용해 평가

lr2 = LinearRegression()
lr2.fit(X_poly, y)

lr2.coef_, lr2.intercept_

(array([0.97906552, 0.94978823]), 2.3405007562628866)

시각화

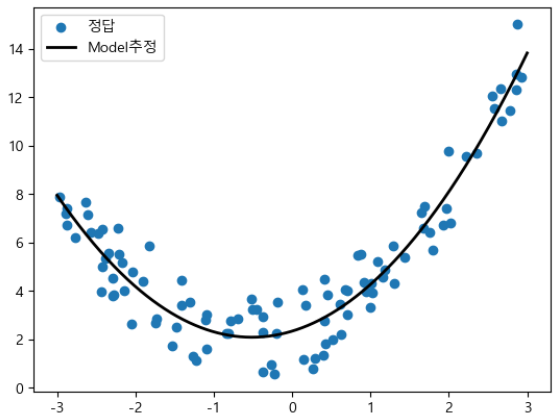
X_new = np.linspace(-3, 3, 1000)[..., np.newaxis] 
# -3에서 3까지의 구간을 1000개의 균등한 간격으로 나눈 숫자 배열을 생성
# 배열에 새로운 축(axis)을 추가. 배열의 마지막 축에 새로운 차원을 추가
# 여기서 ...는 모든 기존 차원을 의미
# 결과적으로, 원래 (1000,) 형태의 1차원 배열이 (1000, 1) 형태의 2차원 배열로 변경
X_new_poly = pnf.transform(X_new)
y_hat = lr2.predict(X_new_poly)

import matplotlib.pyplot as plt
plt.rcParams['font.family'] = "malgun gothic"
plt.rcParams['axes.unicode_minus'] = False
plt.scatter(X, y, label="정답")
plt.plot(X_new, y_hat, color='k', linewidth=2, label="Model추정")
plt.legend()
plt.show()

# 평가
from metrics import print_regression_metrics
print_regression_metrics(y, lr2.predict(X_poly))

MSE: 0.9735576723414217
RMSE: 0.9866902616026073
R Squared: 0.8981478985551461

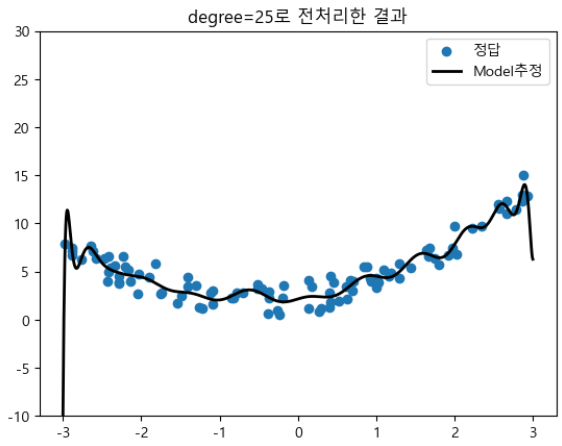
degree를 크게

Feature가 너무 많으면 Overfitting 문제가 생긴다.

pnf3 = PolynomialFeatures(degree=25, include_bias=25)
X_poly3 = pnf3.fit_transform(X)
lr3 = LinearRegression()
lr3.fit(X_poly3, y)

pred3 = lr3.predict(X_poly3)
print_regression_metrics(y, pred3)

MSE: 0.7964961565754771
RMSE: 0.89246633358098
R Squared: 0.9166718011221099

# degree=25 시각화
y_hat = lr3.predict(pnf3.transform(X_new))
plt.scatter(X, y, label="정답")
plt.plot(X_new, y_hat, color='k', linewidth=2, label="Model추정")
plt.legend()
plt.title("degree=25로 전처리한 결과")
plt.ylim(-10, 30)
plt.show()

PolynomialFeatures를 Boston Dataset에 적용

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from metrics import print_regression_metrics

df = pd.read_csv('data/boston_hosing.csv')
X = df.drop(columns='MEDV')
y = df['MEDV']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

# interaction_only=True : 교차항만 추가.
preprocessing = Pipeline(
    steps=[("poly", PolynomialFeatures(degree=2, include_bias=False)), 
            ("scaler", StandardScaler())]
)

X_train_scaled = preprocessing.fit_transform(X_train)
X_test_scaled = preprocessing.transform(X_test)
X.shape, X_train_scaled.shape

((506, 13), (404, 104))

#### 모델링용 파이프라인
pipeline = Pipeline([
    ("preprocess", preprocessing), 
    ("model", LinearRegression())
])

모델 생성 학습 추론 평가

# 학습
pipeline.fit(X_train, y_train)
# 검증
pred_train = pipeline.predict(X_train)
pred_test = pipeline.predict(X_test)

print_regression_metrics(y_train, pred_train, "train set")
print_regression_metrics(y_test, pred_test, "test set")

train set
MSE: 4.340278052012291
RMSE: 2.0833333991496157
R Squared: 0.9490240966612828
test set
MSE: 31.27781497144707
RMSE: 5.592657237078549
R Squared: 0.6158858584078876

규제 (Regularization)

선형 회귀 모델에서 과대적합(Overfitting) 문제를 해결하기 위해 가중치(회귀계수)에 페널티 값을 적용한다.
입력데이터의 Feature들이 너무 많은 경우 Overfitting이 발생.
- Feature수에 비해 관측치 수가 적은 경우 모델이 복잡해 지면서 Overfitting이 발생한다.
해결
- 데이터를 더 수집한다.
- Feature selection
  - 불필요한 Features들을 제거한다.
- 규제 (Regularization) 을 통해 Feature들에 곱해지는 가중치가 커지지 않도록 제한한다.(0에 가까운 값으로 만들어 준다.)
  - LinearRegression의 규제는 학습시 계산하는 오차를 키워서 모델이 오차를 줄이기 위해 가중치를 0에 가까운 값으로 만들도록 하는 방식을 사용한다.
  - L1 규제 (Lasso)
  - L2 규제 (Ridge)

Ridge Regression (L2 규제)

손실함수(loss function)에 규제항으로 $\alpha \sum_{i=1}^{n}{w_{i}^{2}}$ (L2 Norm)을 더해준다.
$\alpha$ 는 하이퍼파라미터로 모델을 얼마나 많이 규제할지 조절한다.
- $\alpha = 0$ 에 가까울수록 규제가 약해진다. (0일 경우 선형 회귀동일)
- $\alpha$ 가 커질 수록 모든 가중치가 작아져 입력데이터의 Feature들 중 중요하지 않은 Feature의 예측에 대한 영향력이 작아지게 된다.

\text{손실함수}(w) = \text{MSE}(w) + \alpha \cfrac{1}{2}\sum_{i=1}^{n}{w_{i}^{2}}

손실함수(Loss Function): 모델의 예측한 값과 실제값 사이의 차이를 정의하는 함수로 모델이 학습할 때 사용된다.

# Ridge, Lasso, LinearRegression - 모델 함수는 동일(WX + b). 
#                                           최적의 parameter(w, b)를 찾는 방법(손실함수)의 차이.
from sklearn.linear_model import Ridge #, Lasso, LinearRegression
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

규제 alpha 에 따른 weight 변화

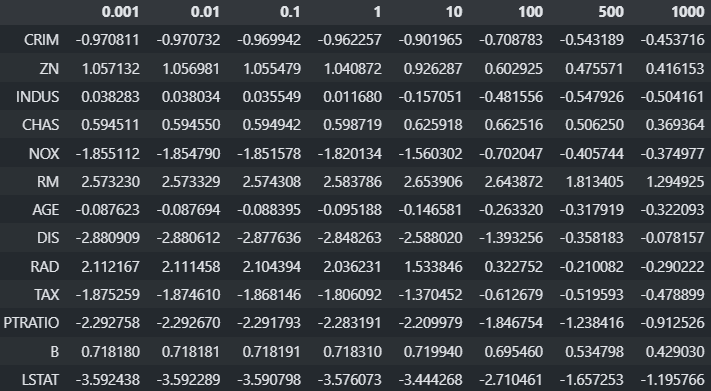
from sklearn.metrics import r2_score
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100, 500, 1000]
# alpha에 따른 각 feature 곱해지는 weight들을 저장할 DataFrame
coef_df = pd.DataFrame() 
bias_list = [] #bias 들 저장할 리스트
for alpha in alpha_list:
    model = Ridge(alpha=alpha, random_state=0)
    model.fit(X_train_scaled, y_train)
    coef_df[f"{alpha}"] = model.coef_
    bias_list.append(model.intercept_)
    # 검증결과 출력
    pred_train = model.predict(X_train_scaled)
    pred_test = model.predict(X_test_scaled)
    print(f"Alpha {alpha} - Train: {r2_score(y_train, pred_train)}, Test: {r2_score(y_test, pred_test)}")

Alpha 0.001 - Train: 0.7730135569106857, Test: 0.5892212945055596
Alpha 0.01 - Train: 0.7730135553534744, Test: 0.5892114815046761
Alpha 0.1 - Train: 0.7730134004374536, Test: 0.589113422273519
Alpha 1 - Train: 0.7729986739069825, Test: 0.5881400471345539
Alpha 10 - Train: 0.772025270378812, Test: 0.5791628807875258
Alpha 100 - Train: 0.7515163225742547, Test: 0.5272685191319562
Alpha 500 - Train: 0.6588192082625857, Test: 0.42879808129182595
Alpha 1000 - Train: 0.5728326430134054, Test: 0.36551722844114254

coef_df.index = X_train.columns
coef_df

Lasso(Least Absolut Shrinkage and Selection Operator) Regression (L1 규제)

손실함수에 규제항으로 $\alpha \sum_{i=1}^{n}{\left| w_i \right|}$ (L1 Norm)더한다.
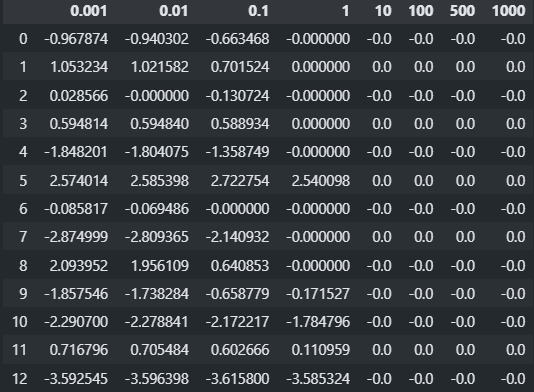
Lasso 회귀의 상대적으로 덜 중요한 특성의 가중치를 0으로 만들어 자동으로 Feature Selection이 된다.

\text{손실함수}(w) = \text{MSE}(w) + \alpha \sum_{i=1}^{n}{\left| w_i \right|}

from sklearn.linear_model import Lasso
from sklearn.metrics import r2_score
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100, 500, 1000]
# alpha에 따른 각 feature 곱해지는 weight들을 저장할 DataFrame
coef_df2 = pd.DataFrame() 
bias_list2 = [] #bias 들 저장할 리스트
for alpha in alpha_list:
    model = Lasso(alpha=alpha, random_state=0)
    model.fit(X_train_scaled, y_train)
    coef_df2[f"{alpha}"] = model.coef_
    bias_list2.append(model.intercept_)
    # 검증결과 출력
    pred_train = model.predict(X_train_scaled)
    pred_test = model.predict(X_test_scaled)
    print(f"Alpha {alpha} - Train: {r2_score(y_train, pred_train)}, Test: {r2_score(y_test, pred_test)}")
Alpha 0.001 - Train: 0.773012729511684, Test: 0.5890287763120774
Alpha 0.01 - Train: 0.7729557113377097, Test: 0.5874763161420908
Alpha 0.1 - Train: 0.7676692732920614, Test: 0.5663726208397636
Alpha 1 - Train: 0.7066864437965619, Test: 0.5069663003862215
Alpha 10 - Train: 0.0, Test: -0.001889737528507185
Alpha 100 - Train: 0.0, Test: -0.001889737528507185
Alpha 500 - Train: 0.0, Test: -0.001889737528507185
Alpha 1000 - Train: 0.0, Test: -0.001889737528507185
coef_df2

PolynormialFeatures로 전처리한 Boston Dataset 에 Ridge, Lasso 규제 적용
X_train_poly = preprocessing.fit_transform(X_train)
X_test_poly = preprocessing.transform(X_test)
X_train_poly.shape
(404, 104)

LinearRegression으로 평가
model1 = LinearRegression()
model1.fit(X_train_poly, y_train)
print_regression_metrics(y_train, model1.predict(X_train_poly), "==========Trainset")
print_regression_metrics(y_test, model1.predict(X_test_poly), "==========Testset")
==========Trainset
MSE: 4.340278052012291
RMSE: 2.0833333991496157
R Squared: 0.9490240966612828
==========Testset
MSE: 31.27781497144707
RMSE: 5.592657237078549
R Squared: 0.6158858584078876

Ridge 의 alpha값 변화에 따른 R square 확인
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
for alpha in alpha_list:
    ridge = Ridge(alpha=alpha, random_state=0)
    ridge.fit(X_train_poly, y_train)
    print(f"{alpha}----------------------------------------")
    print_regression_metrics(y_train, ridge.predict(X_train_poly), "==========Trainset")
    print_regression_metrics(y_test, ridge.predict(X_test_poly), "==========Testset")
0.001----------------------------------------
==========Trainset
MSE: 4.358604290884409
RMSE: 2.087727063311775
R Squared: 0.9488088577825493
==========Testset
MSE: 30.64453953601483
RMSE: 5.535751036310685
R Squared: 0.623662937800885
0.01----------------------------------------
==========Trainset
MSE: 4.455678340160324
RMSE: 2.1108477775908723
R Squared: 0.9476687378885502
==========Testset
MSE: 29.596104880003274
RMSE: 5.440230223069909
R Squared: 0.6365384720502223
0.1----------------------------------------
==========Trainset
MSE: 4.965134623568844
RMSE: 2.228258203972072
R Squared: 0.9416852515894882
==========Testset
MSE: 27.07693766099346
...
==========Testset
MSE: 28.088168621479237
RMSE: 5.2998272256253065
R Squared: 0.6550570176087065
Output is truncated. View as a scrollable element or open in a text editor. Adjust cell output settings...

lasso 의 alpha값 변화에 따른 R square 확인
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
for alpha in alpha_list:
    lasso = Lasso(alpha=alpha, random_state=0)
    lasso.fit(X_train_poly, y_train)
    print(f">>>>>>{alpha}<<<<<<")
    print_regression_metrics(y_train, lasso.predict(X_train_poly), "==========Trainset")
    print_regression_metrics(y_test, lasso.predict(X_test_poly), "==========Testset")
0.001----------------------------------------
==========Trainset
MSE: 5.601080020410676
RMSE: 2.3666600981997132
R Squared: 0.9342161699570151
==========Testset
MSE: 32.532405710830425
RMSE: 5.703718586223414
R Squared: 0.6004785786683159
0.01----------------------------------------
==========Trainset
MSE: 6.269428497823559
RMSE: 2.5038826845169
R Squared: 0.9263665190883612
==========Testset
MSE: 26.15961747471561
RMSE: 5.1146473460753485
R Squared: 0.678741017559849
0.1----------------------------------------
==========Trainset
MSE: 11.926158040527099
RMSE: 3.4534269994495466
R Squared: 0.8599290938988783
==========Testset
MSE: 23.93928952208268
...
==========Testset
MSE: 81.58231743908229
RMSE: 9.032293033282428
R Squared: -0.001889737528507185
Output is truncated. View as a scrollable element or open in a text editor. Adjust cell output settings...

ElasticNet(엘라스틱넷)

릿지와 라쏘를 절충한 모델.
규제항에 릿지, 라쏘 규제항을 더해서 추가한다.
혼합비율 $r$ 을 사용해 혼합정도를 조절
$r=0$ 이면 릿지와 같고 $r=1$ 이면 라쏘와 같다.

\text{손실함수}(w) = \text{MSE}(w) + r\alpha \sum_{i=1}^{n}{\left| w_i \right|} + \cfrac{1-r}{2}\alpha\sum_{i=1}^{n}{w_{i}^{2}}

from sklearn.linear_model import ElasticNet
model = ElasticNet(alpha=0.5, l1_ratio=0.3) # gamma값 0.3
model.fit(X_train_poly, y_train)
print_regression_metrics(y_train, model.predict(X_train_poly), "==========Trainset")
print_regression_metrics(y_test, model.predict(X_test_poly), "==========Testset")
==========Trainset
MSE: 17.932543567258534
RMSE: 4.234683408149721
R Squared: 0.7893850125389811
==========Testset
MSE: 31.77314113785274
RMSE: 5.636766904693926
R Squared: 0.6098028955989219

정리

일반적으로 선형회귀의 경우 어느정도 규제가 있는 경우가 성능이 좋다.
기본적으로 Ridge를 사용한다.
Target에 영향을 주는 Feature가 몇 개뿐일 경우 특성의 가중치를 0으로 만들어 주는 Lasso 사용한다.
특성 수가 학습 샘플 수 보다 많거나 feature간에 연관성이 높을 때는 ElasticNet을 사용한다.

maro

공부 & 프로젝트 & 개발 블로그

이전 포스트

최적화_경사하강법

다음 포스트