📖이진트리(Binary Tree)
이전 시간에 트리에 대하여 정리하였다. 트리는 하나 이상의 노드(node)로 이루어진 자료구조이다. 그렇다면 트리의 일종인 이진트리는 무엇일까?
이진트리는 각각의 노드가 최대 두 개의 자식 노드를 가지는 트리 자료 구조로, 자식 노드를 각각 왼쪽 자식 노드와 오른쪽 자식 노드라고 한다.
각각의 노드가 가질 수 있는 자식 노드의 수가 최대 두 개인 것이 이진트리이다. 즉, 각 노드의 최대 차수가 2인 트리이다.
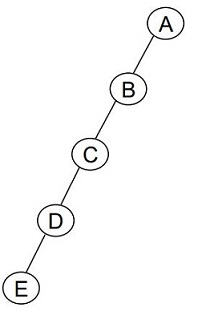
📁편향 이진트리(Skewed Binary Tree)
모든 노드가 한쪽 방향으로만 연결된 트리를 편향 이진트리라고 한다.
📁포화 이진트리(Full Binary Tree)
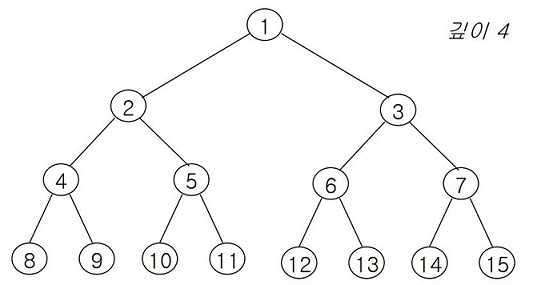
깊이가 k이고, 노드 수가 (2^k - 1)인 이진트리를 포화 이진트리라고 한다. 간단하게 설명하면 리프노드를 제외한 모든 노드가 최대 차수를 갖는 트리이다.
주어진 깊이에 대하여 최대한 노드를 채울 수 있는 만큼 채우는 것이기 때문에 포화라고 한다. 노드에 1부터 (2^k - 1)까지의 번호를 순차적으로 부여할 수 있다.
📁완전 이진트리(Complete Binary Tree)
완전 이진트리는 깊이가 k이고 노드 수가 n일 때, 각 노드들이 깊이가 k인 포화 이진트리에서 1부터 n까지 번호를 붙인 노드와 1대1로 일치한다.
📁이진트리의 배열 표현
이진트리를 표현하는 가장 간단한 방법은 1차원 배열에 노드를 저장하는 것이다. 포화 이진트리에서 노드에 순차적으로 번호를 매긴 것과 같은 개념으로 저장한다.
- 부모 노드의 index : (자식 노드의 index) / 2
- 왼쪽 자식 노드의 index : 2 * (부모 노드의 index)
- 오른쪽 자식 노드의 index : 2 * (부모 노드의 index) + 1
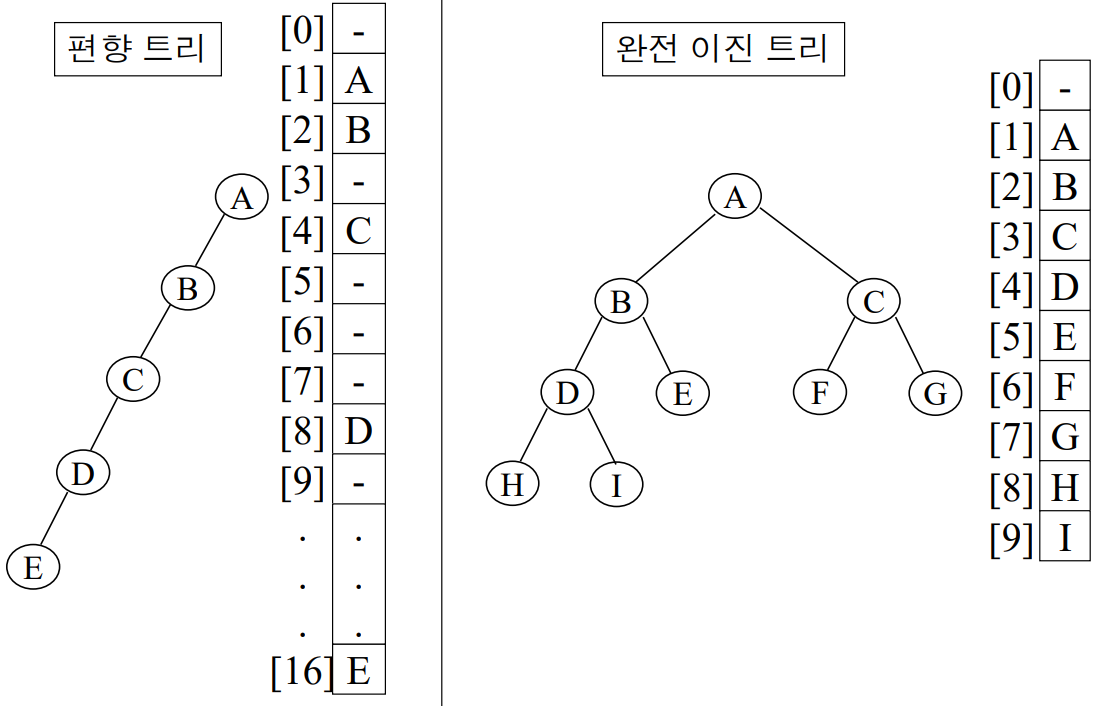
이러한 방식으로 이진트리를 표현하는 경우, 완전 이진트리는 낭비되는 공간이 없지만 편향 이진트리는 공간 낭비가 발생한다.
📁이진트리의 노드 표현
이진트리는 연결리스트의 노드를 이용하여 표현할 수도 있다.
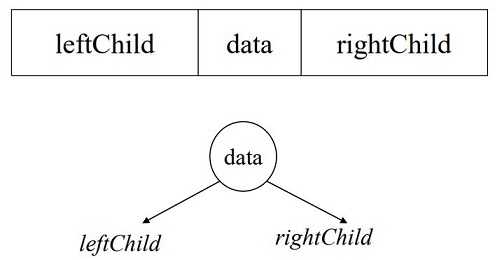
각 노드를 leftChild(왼쪽 자식 노드), data, rightChild(오른쪽 자식 노드)를 저장하는 필드로 구성한다.
이 방법의 경우 data의 부모 노드를 알기 어렵다.
📖이진탐색트리
이진탐색트리 또한 이진트리의 일종으로, 각 노드의 최대 차수가 2이다. 추가된 조건은 다음과 같다.
- 왼쪽 서브트리의 키들은 그 루트의 키보다 작다
- 오른쪽 서브트리의 키들은 그 루트의 키보다 작다
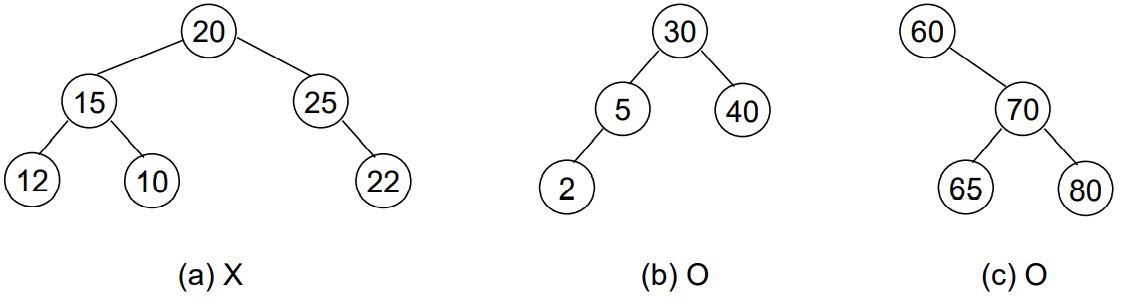
이때, 왼쪽 서브트리와 오른쪽 서브트리도 이진탐색트리이다. 다음과 같은 예시로 개념을 적용해보자.
(a)가 이진탐색트리가 아닌 이유는 10과 22 때문이다.
15의 오른쪽 자식 노드는 15보다 큰 값이어야 한다. 그런데 10이 들어가있으므로 이진탐색트리가 아니다. 이진탐색트리가 되기 위해서는 10이 12의 왼쪽 자식 노드가 되어야 한다.
22도 같은 이유이다. 25의 오른쪽 자식 노드는 25보다 큰 값이어야 하므로 22는 25의 왼쪽 자식 노드가 되어야 한다.
(b)와 (c)를 보면 각 노드의 값보다 왼쪽 자식 노드의 값이 작고, 오른쪽 자식 노드의 값은 크다. 따라서 이진탐색트리이다.
📁이진탐색트리의 탐색
이진탐색트리에서 값 k를 찾는 과정은 다음과 같다.
- k = 노드의 키 : 종료
- k < 노드의 키 : 왼쪽 서브트리 탐색
- k > 노드의 키 : 오른쪽 서브트리 탐색
C++로 구현하면 다음과 같다.
class Node {
public:
int data;
Node* leftChild = nullptr;
Node* rightChild = nullptr;
Node(int input_data, Node* input_leftChild, Node* input_rightChild) {
data = input_data;
leftChild = input_leftChild;
rightChild = input_rightChild;
}
};
Node* BST_Search(Node* node, int k) {
if (node == nullptr) {
return nullptr;
}
if (k == node->data) {
return node;
}
else if (k < node->data) {
return BST_Search(node->leftChild, k); //왼쪽 서브트리 탐색
}
else if (k > node->data) {
return BST_Search(node->rightChild, k); //오른쪽 서브트리 탐색
}
}
📁이진탐색트리의 삽입
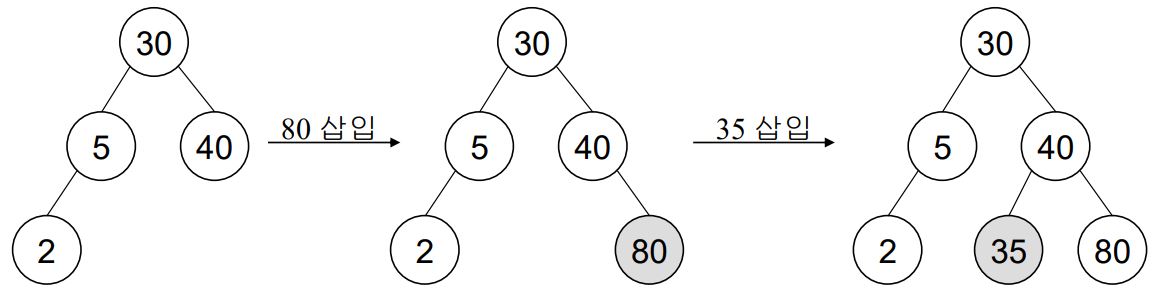
이진탐색트리에서 새로운 값 x를 가진 노드를 삽입하는 과정은 다음과 같다.
- 이진탐색트리에서 x를 값으로 갖는 노드를 탐색
- 탐색이 끝난 지점에 값을 삽입
C++로 구현하면 다음과 같다.
//newNode는 새로 삽입할 노드, tree는 newNode와 값 비교할 이진탐색트리의 노드
void BST_Insert(Node* tree, Node* newNode) {
if (newNode->data < tree->data) {
if (tree->leftChild == nullptr) { //탐색 끝
tree->leftChild = newNode;
return;
}
else {
BST_Insert(tree->leftChild, newNode); //왼쪽 서브트리 탐색
}
}
else if (newNode->data > tree->data) {
if (tree->rightChild == nullptr) { //탐색 끝
tree->rightChild = newNode;
return;
}
else {
BST_Insert(tree->rightChild, newNode); //오른쪽 서브트리 탐색
}
}
}📁이진탐색트리의 삭제
이진탐색트리에서 삭제를 하는 과정은 다음과 같다.
- 리프 노드의 삭제 : 부모 노드의 자식 필드를 초기화
- 하나의 자식 노드를 가진 노드의 삭제 : 삭제된 노드의 자식 노드를 삭제하는 노드의 자리에 위치
- 두 개의 자식 노드를 가진 노드의 삭제 : 왼쪽 서브트리에서 가장 큰 원소나 오른쪽 서브트리에서 가장 작은 원소로 대체
다음은 하나의 자식 노드를 가진 노드를 삭제하는 과정이다.
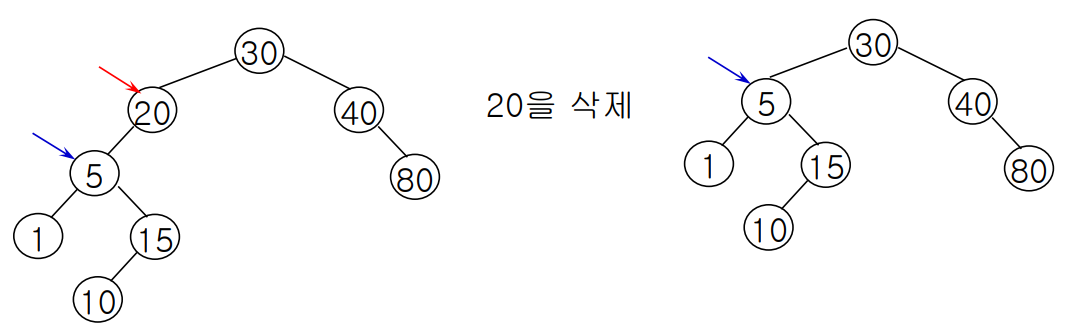
삭제할 20의 자식 노드인 5를 20의 자리에 위치시킨다.
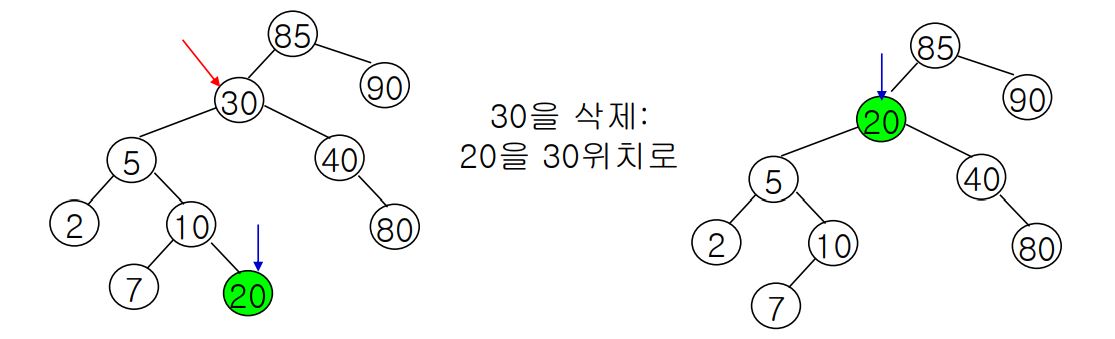
다음은 두 개의 자식 노드를 가진 노드를 삭제하는 과정이다.
30을 삭제하려고 할 때, 30의 왼쪽 서브트리에서 가장 큰 원소인 20으로 노드를 대체한다.
C++로 구현하면 다음과 같다.
//k는 삭제할 노드의 값, node는 k와 값 비교할 노드, parent는 node의 부모 노드
Node* BST_Remove(Node* node, Node* parent, int k) {
if (node == nullptr) {
return nullptr;
}
Node* removeNode = nullptr; //삭제할 노드, 마지막에 반환하기 위해 저장
//삭제할 노드 탐색
if (node->data < k) {
removeNode = BST_Remove(node->rightChild, node, k); //오른쪽 서브트리 탐색
}
else if (node->data > k) {
removeNode = BST_Remove(node->leftChild, node, k); //왼쪽 서브트리 탐색
}
else if (node->data == k) {
removeNode = node; //삭제할 노드 저장
if (node->leftChild == nullptr && node->rightChild == nullptr) { //삭제할 노드가 리프 노드
//부모 노드의 자식 필드 초기화
if (parent->leftChild == node) {
parent->leftChild == nullptr;
}
else {
parent->rightChild == nullptr;
}
}
else if (node->leftChild == nullptr || node->rightChild == nullptr) { //삭제할 노드의 자식 노드가 한 개
Node* newChild = nullptr; //삭제할 노드의 자식 노드
//삭제할 노드의 자식 노드 저장
if (node->leftChild == nullptr) {
newChild = node->rightChild;
}
else {
newChild = node->leftChild;
}
//삭제할 노드의 자식 노드로 대체
if (parent->leftChild == node) {
parent->leftChild = newChild;
}
else {
parent->rightChild == newChild;
}
}
else if (node->leftChild != nullptr && node->rightChild != nullptr) { //삭제할 노드의 자식 노드가 두 개
Node* newChild = node->leftChild; //삭제할 노드의 왼쪽 서브트리에서 가장 큰 원소
while (newChild->rightChild != nullptr) {
newChild = newChild->rightChild;
}
BST_Remove(node, nullptr, newChild->data);
node->data = newChild->data;
}
}
return removeNode;
}