📖해시
해시는 데이터를 효율적으로 다루기 위한 방법 중 하나이다. 자세한 정의는 다음과 같다.
해시(hash)란 임의의 길이의 데이터를 고정된 길이의 데이터로 매핑(mapping)한 값이다.
📁해시 함수와 해시 충돌
임의의 길이의 데이터를 고정된 길이의 데이터로 매핑해주는 것은 해시 함수(hash function)의 역할이다. 매핑 전 데이터를 키(key), 해시 함수를 적용하여 나온 고정된 길이의 값을 해시값 또는 해시라고 한다.

위와 같이 John Smith, Lisa Smith 등의 이름을 해시 함수를 통해 고정된 두 자리 숫자로 매핑한다.
이때, John Smith와 Sandra Dee가 모두 02로 매핑되었다. 이렇게 해시 함수가 서로 다른 두 개의 키를 동일한 해시값으로 매핑하는 것은 해시 충돌이라고 한다.
📁해시 테이블
해시 테이블(hash table)은 해시 함수를 이용하여 키와 값을 매핑하는 자료구조이다.
해시 함수를 사용하여 키를 해시값으로 매핑하고, 이 해시값을 색인(index) 혹은 주소로 삼아 데이터의 값을 키와 함께 저장한다. 이때, 데이터가 저장되는 곳을 버킷(bucket) 또는 슬롯(slot)이라고 한다. 다음과 같이 나타낼 수 있다.
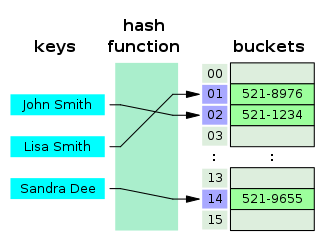
키(이름)을 해시 함수를 통해 해시값(0부터 15까지의 수)로 매핑하고, 이 해시값을 index로 하여 버킷에 전화번호를 저장한다.
이렇게 해시 함수를 이용하면 값이 저장된 위치를 즉시 알아낼 수 있다. 데이터의 양이 아무리 많아지더라도 원리적으로 해시 변환과 검색에 걸리는 시간은 항상 동일하다. 따라서 방대한 데이터에서 특정한 값을 검색할 때 해시 테이블을 사용하면 검색 시간을 획기적으로 단축할 수 있다.
📖해싱
해싱(hashing)은 해시 함수를 사용하여 주어진 값을 변환한 뒤, 해시 테이블에 저장하고 검색하는 기법을 말한다.
일반적으로 특정 데이터가 저장된 위치를 찾아내기 위해서는 데이터가 저장된 자료구조에서 반복 비교를 통해 원하는 데이터인지 확인하는 방법을 사용한다. 그러나, 해시 함수를 통해 데이터를 저장할 경우, 해시 함수에서의 계산으로 바로 데이터가 저장된 위치를 찾아낼 수 있다.
📁제산법
제산법(division)은 나머지 연산을 통해 해시값을 계산하는 방법이다.
키 값 % 전체 버킷의 크기 = 인덱스
키 값을 특정 정수로 나눈 나머지를 인덱스로 하여 해시 테이블에 키 값을 저장한다. 이때, 해시 충돌을 피하기 위해 키 값을 나누는 정수는 소수인 것이 좋다.
따라서 일반적으로 해시 테이블(버킷)의 크기를 소수로 하거나 해시 테이블의 크기보다 큰 정수 중 가장 작은 소수로 나머지 연산을 한다.
📁중간제곱법
중간제곱법(mid-square)는 키 값을 제곱한 결과의 중간 부분 몇 비트를 인덱스로 사용한다.
제곱한 값의 중간 비트들은 키의 모든 비트의 영향을 받으므로 서로 다른 키는 서로 다른 결과값을 도출할 확률이 높다. 이때, 인덱스로 사용하는 비트의 수는 전체 버킷의 크기에 따라 달라진다.

위와 같이 키 값을 제곱한 결과의 중간 8비트를 인덱스로 한다고 가정하면 1110 1001의 10진수 값인 233이 인덱스가 된다. 이렇게 인덱스로 사용하는 비트의 수가 8이면 전체 버킷의 크기는 256개일 것을 예상할 수 있다.
📁폴딩법
폴딩법(folding)은 키 값을 여러 부분으로 나눈 후, 각 부분의 값을 더하거나 XOR(배타적 논리합) 연산을 한 값을 인덱스로 한다.
- 이동 폴딩(Shift Folding) : 각 부분의 값들을 좌측 또는 우측 끝자리에 맞춰 더한다
- 경계 폴딩(Boundary Folding) : 각 부분의 경계선을 역으로 정렬하여 더한다
다음과 같이 키 값을 5개로 나눌 수 있다.
이동 폴딩(우측 끝자리에 맞춤) : P1+P2+P3+P4+P5 = 301+230+123+213+30 = 897
경계 폴딩 : P1+P2(역)+P3+P4(역)+P5 = 301+032+123+312+30 = 798
📁숫자분석법
숫자분석법(digit-analysis)는 키를 구성하는 숫자가 모든 키들 내에서 어떻게 분포되어있는지 조사하고, 숫자가 고르게 분포되어 있는 자리를 필요한만큼 선택해 인덱스로 사용한다.
예를 들어, 다음과 같은 전화번호를 키 값으로 하고, 인덱스는 3자리 수라고 가정하자.
012 - 452 - 0236 ==> 426
012 - 153 - 0530 ==> 150
015 - 342 - 0935 ==> 395
012 - 752 - 1032 ==> 702
012 - 852 - 0470 ==> 840
012 - 543 - 0231 ==> 512
먼저, 첫번째~세번째 자리 수는 거의 012로 동일하므로 제외한다. 이외의 분포를 살펴보면 5번, 6번, 7번, 9번 자리 수 또한 같은 숫자가 많이 분포되어있다. 따라서 4번, 8번, 10번 자리의 수를 선택하여 인덱스로 사용한다.
📁기수변환법
기수변환법(radix-exchange)는 키를 다른 진법으로 간주하고 키를 변환해 인덱스를 얻는다.
변환된 인덱스가 전체 버킷의 크기를 초과할 시, 인덱스의 최하위 자리부터 전체 버킷의 크기가 허용하는 자릿수만큼 취해 인덱스로 사용한다.
10진수 13479
=> 16진수로 간주, 16진수 13479를 10진수로 변환 : 78969
