문제

백준 9461번
https://www.acmicpc.net/problem/9461

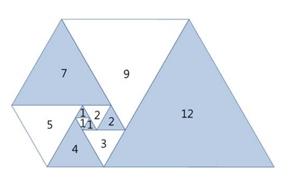
그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 변의 길이를 k라 했을 때, 그 변에 길이가 k인 정삼각형을 추가한다.

파도반 수열 P(N)은 나선에 있는 정삼각형의 변의 길이이다. P(1)부터 P(10)까지 첫 10개 숫자는 1, 1, 1, 2, 2, 3, 4, 5, 7, 9이다.

N이 주어졌을 때, P(N)을 구하는 프로그램을 작성하시오.

---

생각하기

재귀함수를 사용해서 문제를 쉽게 풀 수 있었다.
삼각형의 가장 큰 변을 찾는 규칙은 간단하다.

N번째 위치의 삼각형의 변의 길이를 찾는다고 했을 때,
N-3번째 위치 + N-2번째 위치의 삼각형 변의 길이합이 N번째 변의 길이 값이된다.

동작

	static long DP(long depth) {
		// 가장 긴변을 찾아야 함
		// 만들려는 가장 긴 변은 memoization[depth-3] + memoization[depth-2]의 값이다.
		
		for(int i=4; i<=depth; i++) {
			if(memoization[i] == 0) {				
				memoization[i]= DP(i - 3) + DP(i - 2);
			}
		}

		return memoization[(int) depth];
	} // End of DP

재귀 구조는 그냥 반복되는 규칙되로 depth의 값 까지 반복하며
DP의 함수값을 memoization 배열에 저장해 나가면 된다.

---

코드

import java.io.*;

public class Main {
	static long memoization[] = new long[101];

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringBuilder sb = new StringBuilder();

		memoization[1] = 1;
		memoization[2] = 1;
		memoization[3] = 1;
		int T = Integer.parseInt(br.readLine());
		while(T-->0) {
			int N = Integer.parseInt(br.readLine());

			sb.append(DP(N)).append('\n');
		}

		System.out.println(sb);
	} // End of main

	static long DP(long depth) {
		// 가장 긴변을 찾아야 함
		// 만들려는 가장 긴 변은 memoization[depth-3] + memoization[depth-2]의 값이다.
		
		for(int i=4; i<=depth; i++) {
			if(memoization[i] == 0) {				
				memoization[i]= DP(i - 3) + DP(i - 2);
			}
		}

		return memoization[(int) depth];
	} // End of DP
} // End of Main class