그래프(Graph)
- 비선형 자료구조
- 비선형 자료구조(Non-linear Data Structure)란 데이터를 일렬으로 구성하지 않고, 자료 순서나 관계가 복잡한 자료구조를 말한다.
- 자료를 계층적으로 구성한 자료구조로, 데이터가 일렬로 연결되는 선형 자료구조와 달리 분기점이나 사이클 등이 존재하여 비선형적인 구조를 가지고 있다.
- 선형 자료구조보다 복잡한 구조를 가지기 때문에 구현 및 관리가 어려울 수 있지만, 적절하게 활용하면 다양한 문제를 해결할 때 도움이 된다.
- 대표적인 비선형 자료구조로는 트리, 그래프, 맵, 해시테이블 등이 있다.
- 정점(node 또는 vertex)과 간선(edge)로 이루어진 자료구조
그래프 G를 G=(V,E)로 정의하는데, V는 정점의 집합, E는 간선들의 집합을 의미한다. - 연결되어 있는 객체 간의 관계를 표현할 수 있는 자료구조
- 지도, 지하철 노선도의 최단 경로, 전기 회로의 소자들, 도로(교차점과 일방 통행길), 선수과목 등
그래프의 특징
- 그래프는 네트워크 모델 이다.
- 2개 이상의 경로가 가능하다.
- 즉, 노드들 사이에 무방향/방향에서 양방향 경로를 가질 수 있다.
- self-loop 뿐 아니라 loop/circuit 모두 가능하다.
- 루트 노드라는 개념이 없다.
- 부모-자식 관계라는 개념이 없다.
- 순회는 DFS나 BFS로 이루어진다.
- 그래프는 순환(Cyclic) 혹은 비순환(Acyclic)이다.
- 그래프는 크게 방향 그래프와 무방향 그래프가 있다.
- 간선의 유무는 그래프에 따라 다르다.
- 사이클(Cycle)
- 단순 경로의 시작 정점과 종료 정점이 동일한 경우
- 단순 경로: 경로 중에서 반복되는 정점이 없는 경우
- 차수(Degree)
- 한 노드에 인접한 간선의 수
- 무방향 그래프에서는 노드의 차수가 연결된 노드의 수와 같다.
- 방향 그래프에서는 인접한 노드의 수와 나가는 노드의 수로 구분된다.
그래프의 종류
무방향 그래프(Undirected Graph)
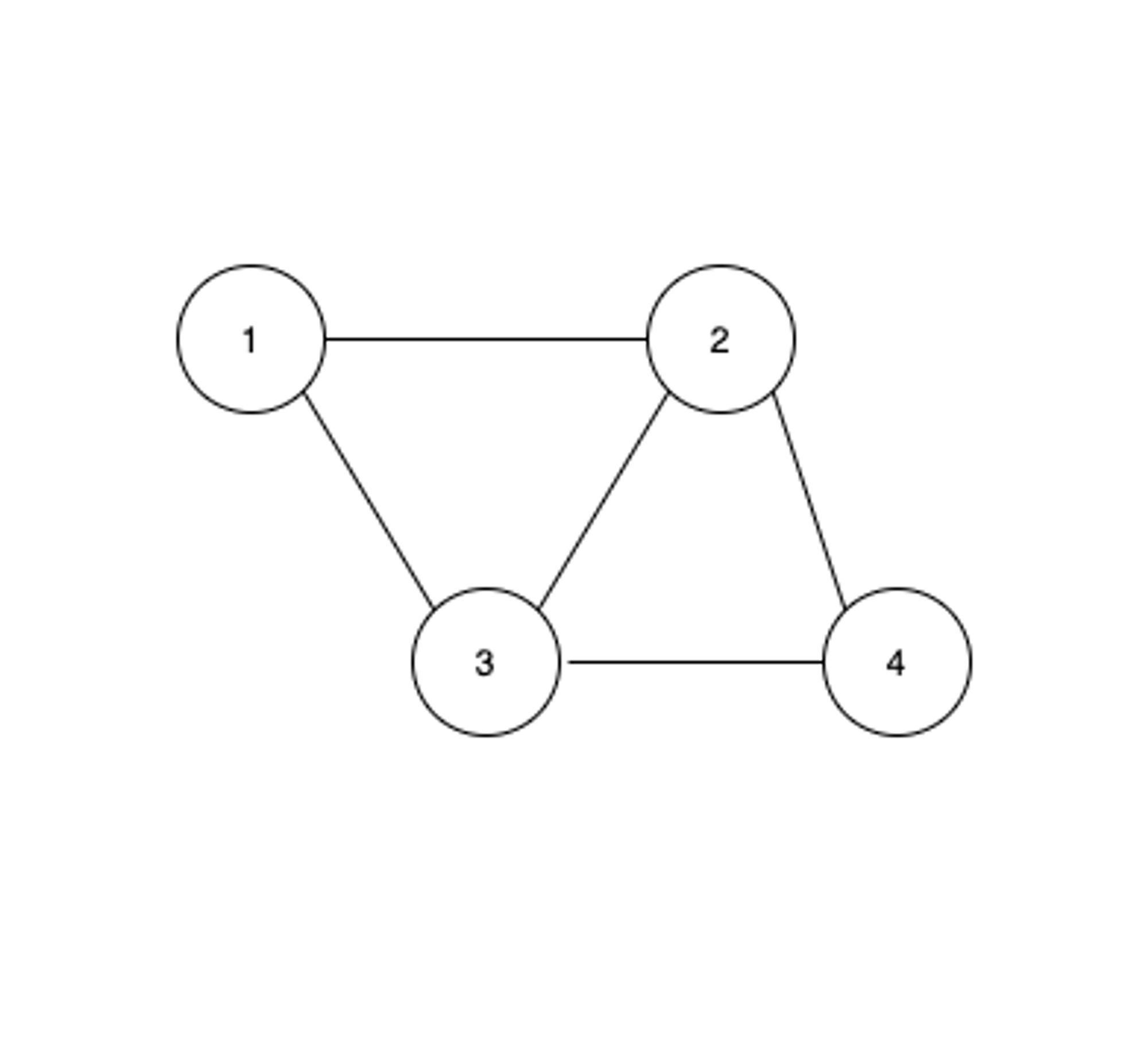
- 두 정점을 연결하는 간선에 방향이 없는 그래프
- 양쪽 방향으로 모두 이동할 수 있다.
- 방향의 강제하는 일방통행이 없다.
- 정점 A와 정점 B를 연결하는 간선은 (A, B)와 같이 정점의 쌍으로 표현한다. (A, B)는 (B, A) 동일하다.
방향 그래프(Directed Graph)
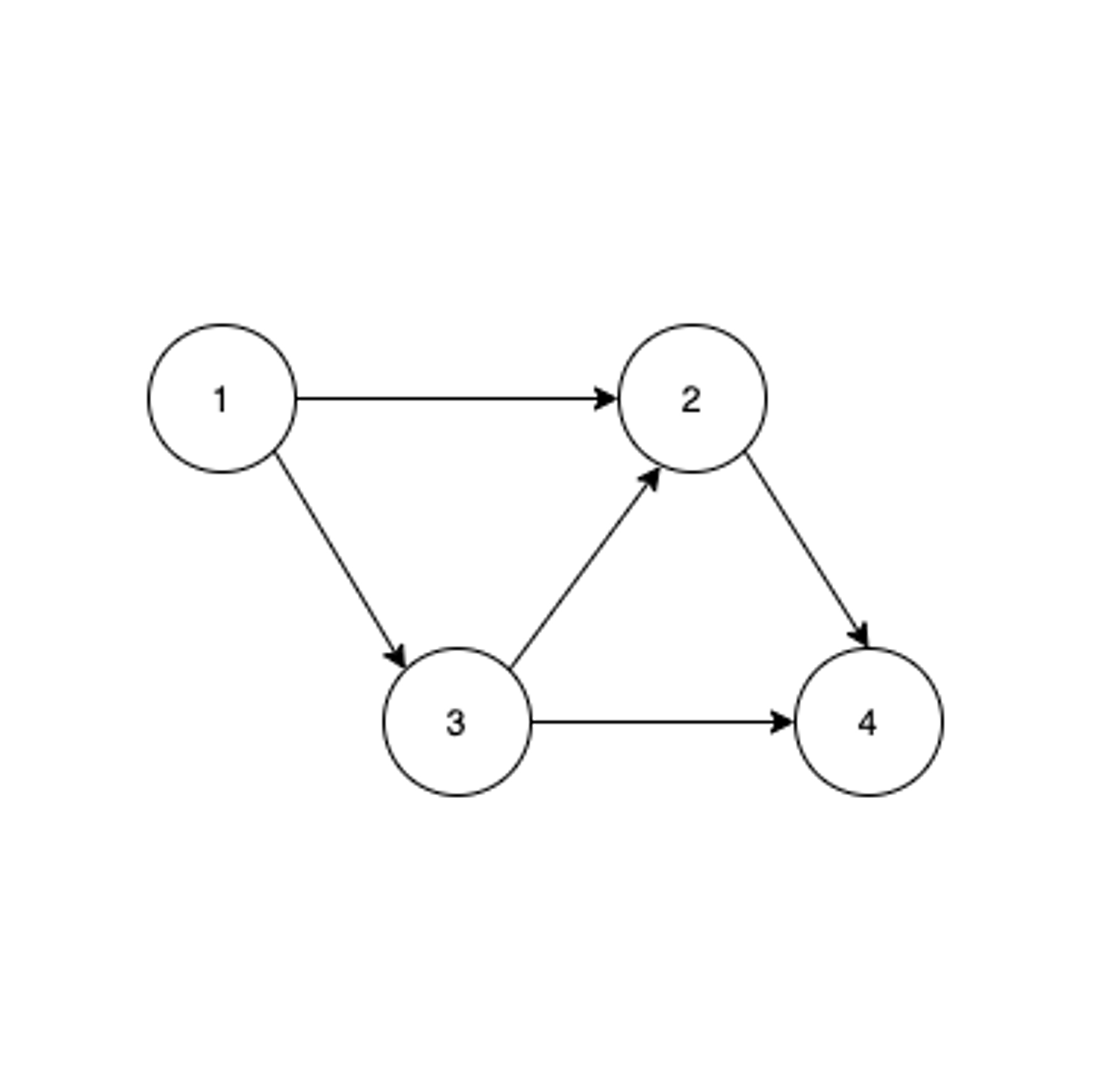
- 두 정점을 연결하는 간선에 방향이 존재하는 그래프
- 간선이 가리키는 방향(한쪽 방향)으로만 이동 가능
가중치 그래프(Weighted Graph)
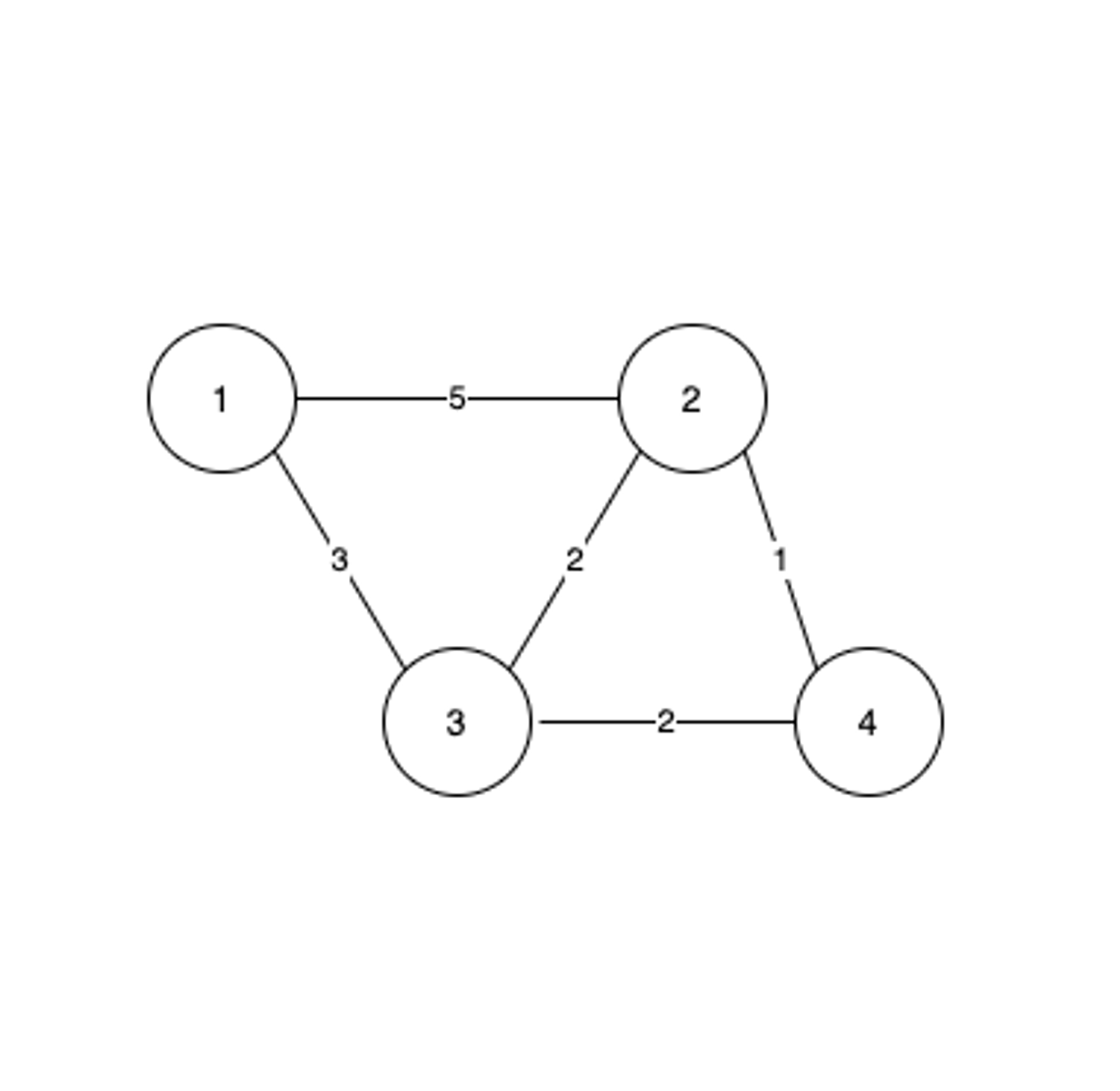
- 간선에 비용이나 가중치가 할당되어, 정점을 이동할 때 비용이 드는 그래프
- '네트워크(Network)'라고도 한다.
- 도시-도시의 연결, 도로의 길이, 회로 소자의 용량, 통신망의 사용료 등
- 도시-도시의 연결, 도로의 길이, 회로 소자의 용량, 통신망의 사용료 등
완전 그래프(Complete Graph)

- 모든 정점이 간선으로 서로 연결된 그래프
- 무방향 완전 그래프의 정점 수가 n이면,
간선의 수는 n * (n - 1) / 2 - 완전 그래프는 항상 연결 그래프를 포함한다.
부분 그래프(Sub Graph)
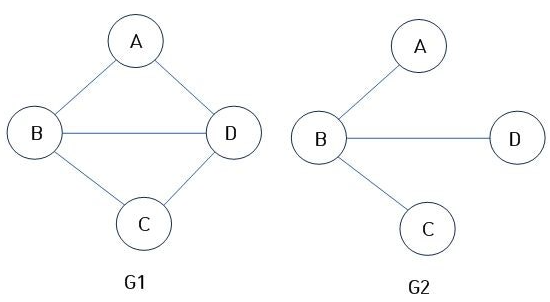
- 주어진 그래프의 일부 노드와 간선으로 이루어진 그래프
- G2는 G1의 부분 그래프이다.
연결 그래프(Connected Graph)
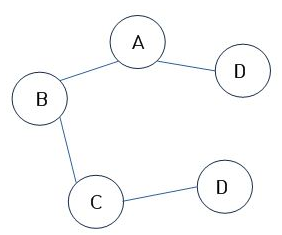
- 무방향 그래프에 있는 모든 정점쌍에 대해서 항상 경로가 존재하는 그래프
- 예) 트리(Tree): 사이클을 가지지 않는 연결 그래프
비연결 그래프(Disconnected Graph)
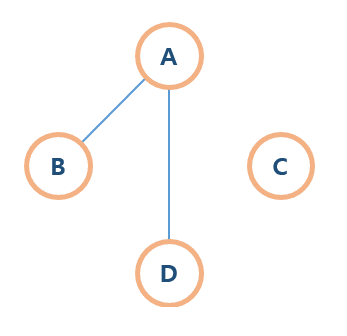
- 무방향 그래프에서 특정 정점쌍 사이에 경로가 존재하지 않는 그래프
순환 그래프(Acyclic Graph)

- 사이클이 있는 그래프
비순환 그래프(Acyclic Graph)
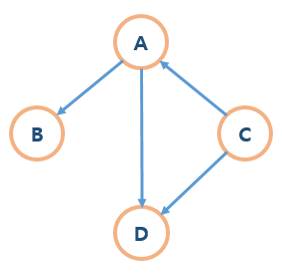
- 사이클이 없는 그래프
그래프의 장단점
장점
- 복잡한 관계를 직관적으로 표현할 수 있다.
- 네트워크 구조를 표현할 수 있어서 소셜 네트워크, 전력망, 노선도 등의 문제를 다룰 수 있다.
- 다양한 최적화 문제를 풀 수 있다.
예를 들어, 최단 경로 문제나 최소 신장 트리 문제 등 다양한 그래프 알고리즘을 사용하여 최적화 문제를 풀 수 있다.
단점
- 데이터의 규모가 커질수록 계산 비용이 증가한다. 대형 그래프에서는 탐색 비용과 알고리즘의 수행 시간 등이 중요한 문제가 될 수 있다.
- 그래프의 구성이 복잡하면 이를 이해하기 어려울 수 있다.
- 방향성 그래프에서는 경로의 유무가 중요하므로, 경로가 존재하지 않는 경우에는 이를 고려하여 알고리즘을 설계해야 한다.
단점의 보완
- 분할 정복, 동적 계획법 등의 최적화 알고리즘을 사용하여, 계산 비용을 줄일 수 있다.
- 복잡해진 그래프를 시각화하는 방법을 고민하여, 데이터의 시각적 이해를 돕는 방법이 있다.
- 그래프를 단순화하여, 경로가 존재하지 않는 경우에도 유용한 결과를 도출할 수 있도록 만든다.
예를 들면, 가중치를 조절하여 일정 이하의 가중치를 가진 간선들은 무시하는 방법을 생각할 수 있다.
그래프의 구현
- 그래프는 인접 행렬 또는 인접 리스트로 구현할 수 있다.
인접 행렬
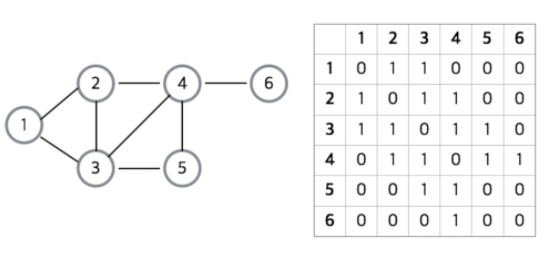
- 그래프의 정점을 2차원 배열로 만든 것
- 정점 간에 직접 연결되어 있다면 1 , 아니라면 0 을 저장
장점
- 2차원 배열에 모든 정점의 간선 정보가 담겨있기 때문에 두 정점에 대한 연결을 조회할 때는 𝑂(1)의 시간 복잡도를 가진다.
- 인접 리스트에 비해 구현이 쉽다.
단점
- 모든 정점에 대해 간선 정보를 입력해야 하므로 인접 행렬을 생성할 때는 𝑂(𝑛^2)의 시간 복잡도가 소요된다.
- 항상 2차원 배열이 필요하므로 필요 이상의 공간이 낭비된다.
인접 리스트
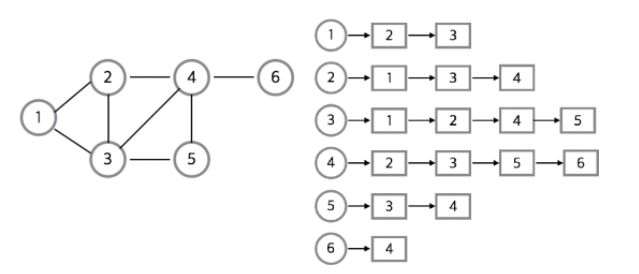
- 인접 리스트는 그래프의 노드를 리스트로 표현한 것이다. 주로 정점의 리스트 배열을 만들어서 관계를 설정한다.
장점
- 정점들의 연결 정보를 탐색할 때 O(n)의 시간 복잡도가 소요된다. (n은 간선의 개수)
- 필요한 만큼 공간을 사용하기 때문에 인접 행렬에 비해 상대적으로 공간의 낭비가 적다.
단점
- 특정 두 정점이 연결되어 있는지 확인하기 위해서는 인접 행렬에 비해 시간이 오래 걸린다.
- 구현이 인접 행렬에 비해 어렵다.
그래프의 탐색
1) 깊이 우선 탐색(DFS)
2) 너비 우선 탐색(BFS)
참고
https://gmlwjd9405.github.io/2018/08/13/data-structure-graph.html
https://leejinseop.tistory.com/43
https://80000coding.oopy.io/125156cf-79bb-48da-82ae-1f2ee7896bb8
https://velog.io/@kwontae1313/%ED%8A%B8%EB%A6%AC%EC%99%80-%EA%B7%B8%EB%9E%98%ED%94%84%EC%97%90-%EB%8C%80%ED%95%B4-%EC%95%8C%EC%95%84%EB%B3%B4%EC%9E%90
https://hongcoding.tistory.com/78
