[자료구조] 트리(Tree)

limce·2024년 5월 23일

자료구조

목록 보기

8/10

트리(Tree)

노드들이 나무 가지처럼 연결된 비선형 계층적 자료구조
- 예) 디렉터리 구조, 조직도
힙을 구현하는 방법 중 하나가 트리
OS의 FileSystem 구조나 대용량의 데이터를 계층적으로 저장할 때 많이 쓰이는 자료구조

트리의 특징

하나의 루트 노드와 0개 이상의 하위 트리로 구성되어 있다.
노드(Node)들과 노드들을 연결하는 간선(Edge)들로 구성
트리내에 또 다른 트리가 있는 재귀적 자료구조
단순 순환(Loop)을 갖지 않고, 연결된 무방향 그래프 구조
그래프의 한 종류이다. '최소 연결 트리'라고도 불린다.
- 사이클(Cycle)이 존재하지 않는
  하나의 연결 그래프(Connected Graph)
- 또는 DAG(Directed Acyclic Graph, 방향성이 있는 비순환 그래프)의 한 종류
노드 간에 부모 자식 관계를 갖고 있는 계층형 자료구조이며 모든 자식 노드는 하나의 부모 노드만 갖는다.
노드가 n개인 트리는 항상 n-1개의 간선(edge)을 가진다.
루트에서 어떤 노드로 가는 경로는 유일하다.
임의의 두 노드 간의 경로도 유일하다.
즉, 두 개의 정점 사이에 반드시 1개의 경로만을 가진다.

트리의 종류

편향 트리

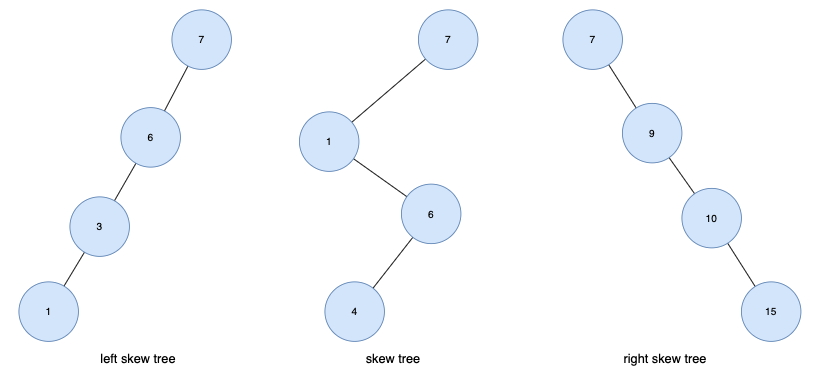
하나의 차수만 가진 경우
즉, 모든 노드들이 자식을 하나만 가진 트리
왼쪽 방향으로 자식을 하나씩만 가질 때 left skew tree,
오른쪽 방향으로 하나씩만 가질 때 right skew tree

이진 트리(Binary Tree)

각 노드의 차수(자식 노드)가 2 이하인 트리

이진 탐색 트리(Binary Search Tree, BST)

순서화된 이진 트리
모든 노드가 아래와 같은 특정 순서를 따르는 속성이 있는 트리
- 모든 왼쪽 자식들 < n <= 모든 오른쪽 자식들 (모든 노드 n에 대해서 반드시 참)
모든 노드는 중복된 값을 갖지 않는다.

m 원 탐색 트리(m-way search tree)

최대 m개의 서브 트리를 갖는 탐색 트리
이진 탐색 트리의 확장된 형태로 높이를 줄이기 위해 사용

균형 트리(Balanced Tree, B-Tree)

O(logN) 시간에 insert와 find를 할 수 있을 정도로 균형이 잘 잡혀 있는 경우
- 예) 레드-블랙 트리, AVL 트리
height-balanced m-way tree라고도 한다.

완전 이진 트리(Complete Binary Tree)

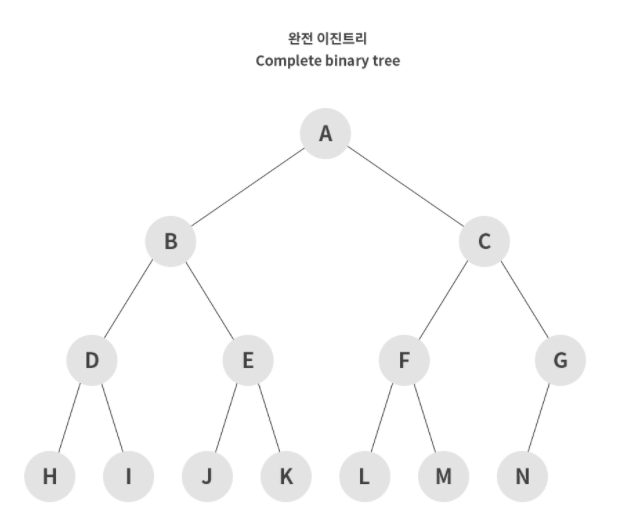
트리의 모든 높이에서 노드가 꽉 차 있는 이진 트리.
즉, 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있다.
마지막 레벨은 꽉 차 있지 않아도 되자만 노드가 왼쪽에서 오른쪽으로 채워져야 한다.
마지막 레벨 h에서 (1 ~ 2h-1)개의 노드를 가질 수 있다.
완전 이진 트리는 배열을 사용해 효율적으로 표현 가능

전 이진 트리(Full Binary Tree 또는 Strictly Binary Tree)

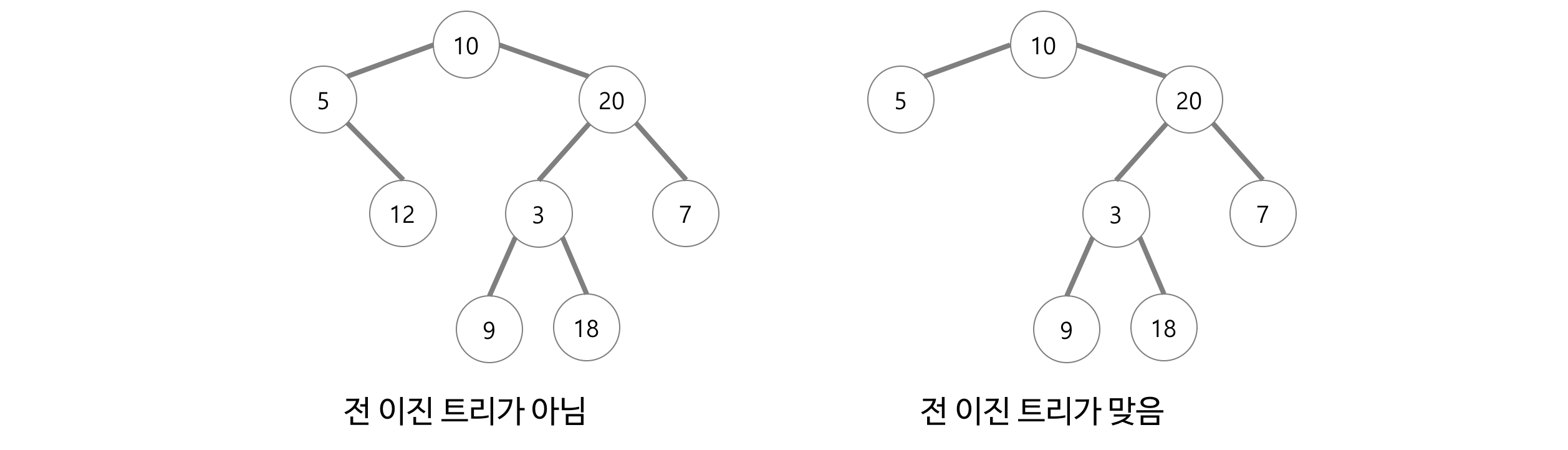
모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리

포화 이진 트리(Perfect Binary Tree)

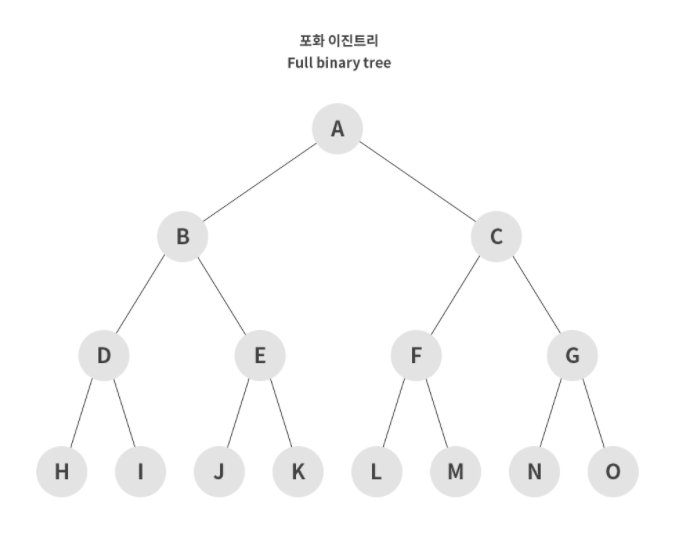
전 이진 트리이면서 완전 이진 트리인 경우
모든 말단 노드는 같은 높이에 있어야 하며, 마지막 단계에서 노드의 개수가 최대가 되어야 한다.
모든 내부 노드가 두 개의 자식 노드를 가진다.
모든 말단 노드가 동일한 깊이 또는 레벨을 갖는다.
노드의 개수가 정확히 2^(k-1)개여야 한다. (k: 트리의 높이)

이진 힙(최소힙과 최대힙)

최소힙(Min Heap)

트리의 마지막 단계에서 오른쪽 부분을 뺀 나머지 부분이 가득 채워져 있는 완전 이진 트리이며, 각 노드의 원소가 자식들의 원소보다 작다.
- 즉, key(부모 노드) >= key(자식 노드)인 완전 이진 트리
- 가장 큰 값은 루트 노드
- N개가 힙에 들어가 있으면 높이는 log(N)이다.

최대 힙(Max Heap)

원소가 내림차순으로 정렬되어 있다는 점에서만 최소힙과 다르다.
각 노드의 원소가 자식들의 원소보다 크다.

트라이(trie, Prefix Tree)

n-차 트리(n-ary Tree)의 변종
각 노드에 문자를 저장하는 자료구조
- 따라서 트리를 아래쪽으로 순회하면 단어 하나가 나온다.
접두사를 빠르게 찾아보기 위한 흔한 방식으로, 모든 언어를 트라이에 저장해 놓는 방식이 있다.
유효한 단어 집합을 이용하는 많은 문제들은 트라이를 통해 최적화할 수 있다.

트리의 순회

전위 순회(Preorder)

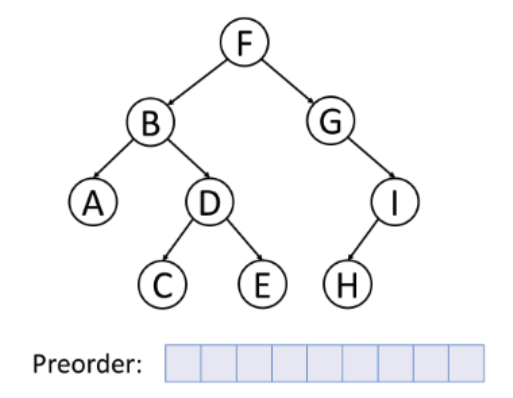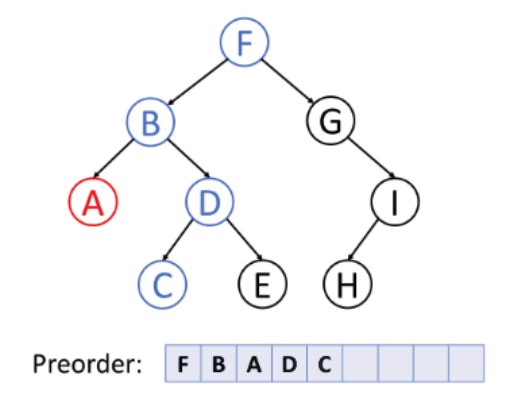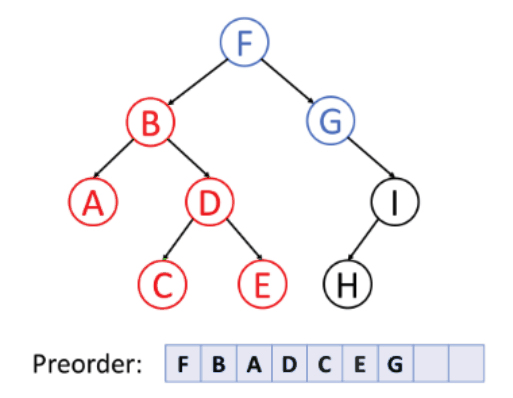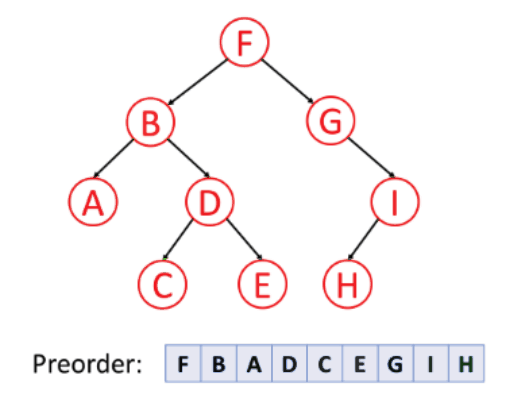
루트노드 --> 왼쪽 서브트리 --> 오른쪽 서브트리의 순서로 순회하는 방식이다. 깊이 우선 순회라고도 불린다.

중위 순회(Inorder)

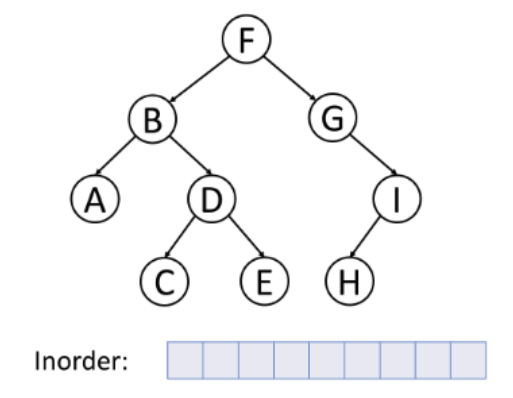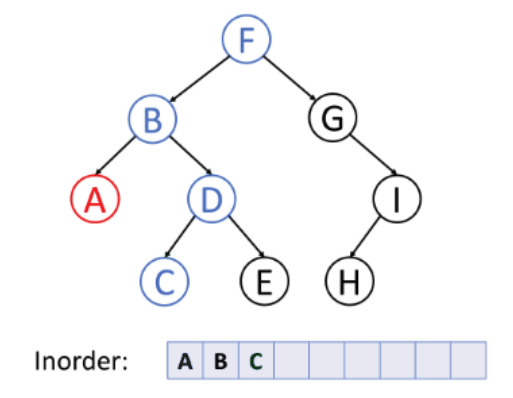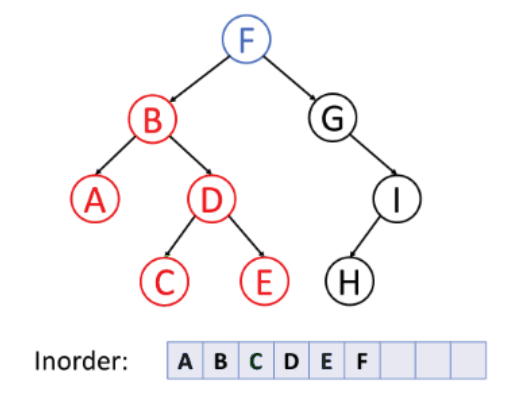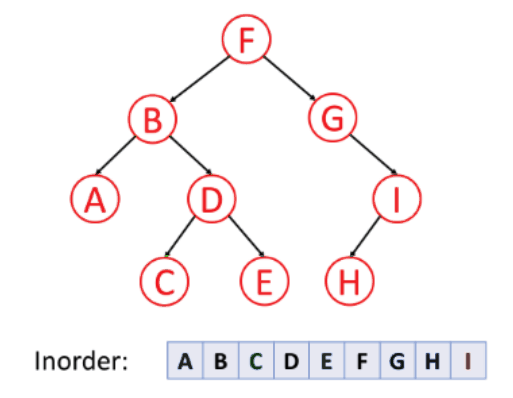
왼쪽 서브트리 --> 노드 --> 오른쪽 서브트리의 순서로 순회하는 방식이다. 대칭 순회라고도 불린다.

후위 순회 (Postorder)

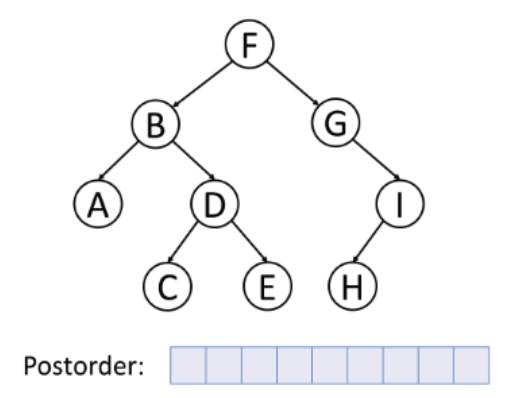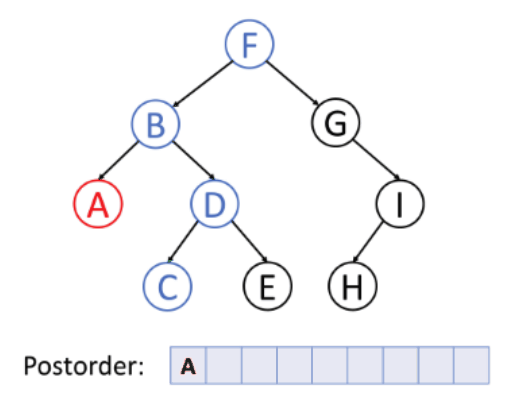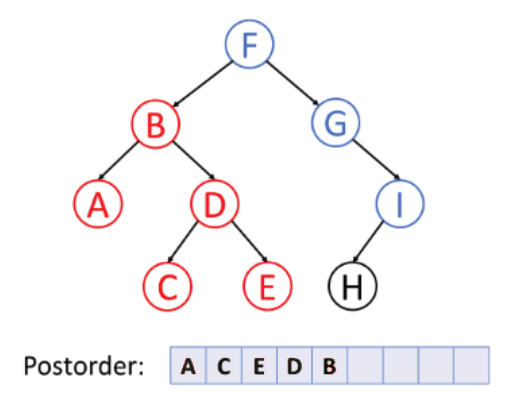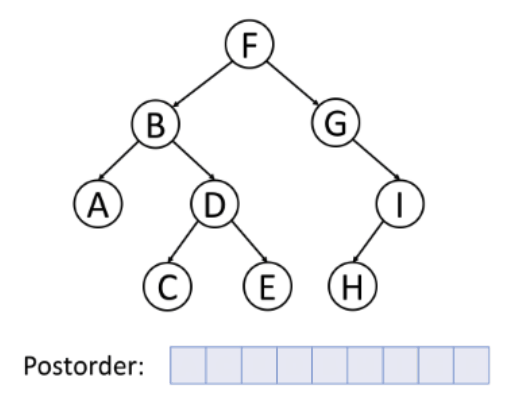
왼쪽 서브트리 --> 오른쪽 서브트리 --> 루트노드의 순서로 순회하는 방식이다.

트리의 구현

트리는 그래프의 한 종류이므로 그래프의 구현 방법(인접 리스트 또는 인접 배열)으로 구현할 수 있다.

인접 배열

1) 1차원 배열에 자신의 부모 노드만 저장하는 방법

트리는 부모 노드를 0개 또는 1개를 가지기 때문
부모 노드가 0개: 루트 노드

2) 이진 트리의 경우, 2차원 배열에 자식 노드를 저장하는 방법

이진 트리는 각 노드가 최대 두 개의 자식을 갖는 트리이기 때문
예) A[i][0]: 왼쪽 자식 노드, A[i][1]: 오른쪽 자식 노드

인접 리스트

1) 가중치가 없는 트리의 경우

ArrayList< ArrayList > list = new ArrayList<>();

2) 가중치가 있는 트리의 경우

1) class Node { int num, dist; // 노드 번호, 거리 } 정의
2) ArrayList[] list = new ArrayList[정점의 수 + 1];

이진 탐색 트리의 구현

[28, 21, 15, 14, 32, 25, 18, 11, 30, 19]를 이진 탐색 트리의 형태로 만들어보자.

이진 탐색 트리로 데이터를 효율적으로 검색(탐색)할 수 있다.
원하는 값을 찾을 때까지 현재의 노드값보다 찾고자하는 값이 작으면 왼쪽으로 움직이고, 크면 오른쪽으로 움직인다.

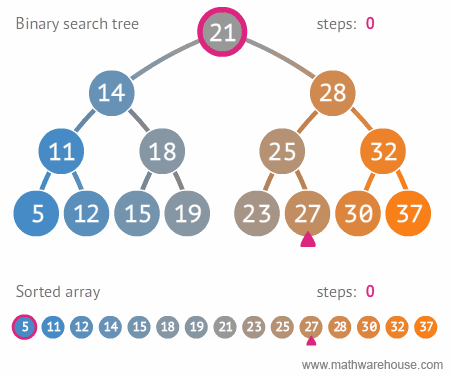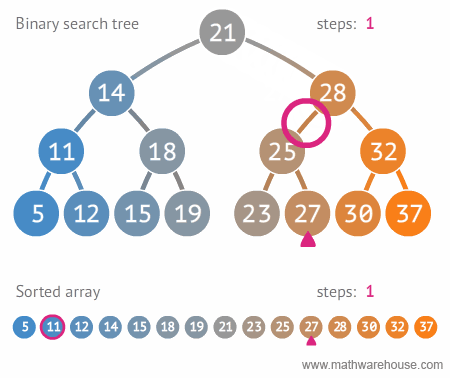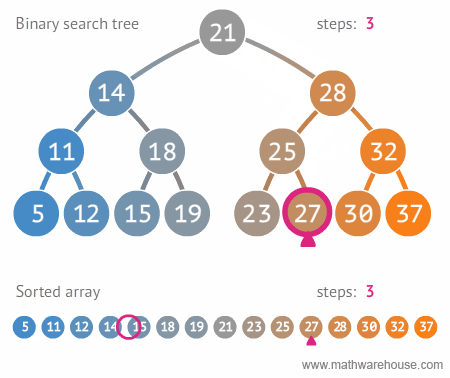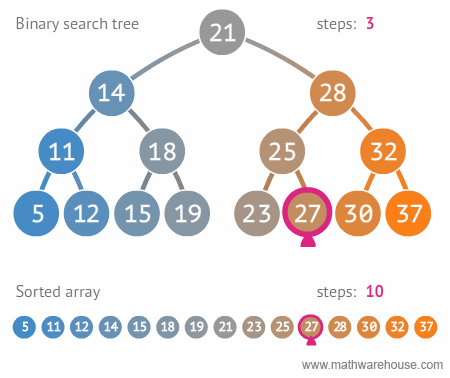
이진 탐색 트리 구현 코드

#pragma once
#include <queue>
#include <iostream>

class Node {
public:
    int value;
    Node* left;
    Node* right;
    Node(const int& value) : value(value) {}
};

class BinarySearchTree {
private:
    Node* root;

    Node* _find(Node* cursor, const int& value) {
        if (!cursor) {
            return nullptr;
        }

        if (cursor->value == value) {
            return cursor;
        }
        else {
            if (cursor->value > value) {
                return _find(cursor->left, value);
            }
            else {
                return _find(cursor->right, value);
            }
        }
    }

    void _insert(Node* cursor, const int& value) {
        Node* parent;
        while (cursor) {
            parent = cursor;
            if (parent->value > value) {
                cursor = cursor->left;
            }
            else {
                cursor = cursor->right;
            }
        }
        if (parent->value > value) {
            parent->left = new Node(value);
        }
        else if (parent->value < value) {
            parent->right = new Node(value);
        }
        else {
            std::cout << "이미 있는 값입니다." << std::endl;
        }
    }

    void _preorderTraversal(Node* cursor) {
        if (!cursor) {
            return;
        }
        
        std::cout << cursor->value << " ";
        this->_preorderTraversal(cursor->left);
        this->_preorderTraversal(cursor->right);
    }

public:
    void insert(const int& value) {
        if (!this->root) {
            this->root = new Node(value);
            return;
        }

        this->_insert(this->root, value);
    }

    Node* find(const int& value) {
        Node* cursor = this->root;
        if (!cursor) {
            return nullptr;
        }
        return this->_find(cursor, value);
    }

    void remove(const int& value) {
        Node* parent;
        Node* deleteTarget;
        Node* cursor = this->root;
        while (cursor) {
            // 노드를 삭제하기 위해서 부모값을 저장해둔다.
            if (cursor->left) {
                if (cursor->left->value == value) {
                    parent = cursor;
                }
            }
            else if (cursor->right) {
                if (cursor->right->value == value) {
                    parent = cursor;
                }
            }

            // 삭제할 노드를 탐색한다.
            if (cursor->value == value) {
                deleteTarget = cursor;
                break;
            }
            else if (cursor->value > value) {
                cursor = cursor->left;
            }
            else {
                cursor = cursor->right;
            }
        }

        // 자식노드가 하나도 없을 때
        if (deleteTarget->right == nullptr && deleteTarget->left == nullptr) {
            if (parent->left == deleteTarget) {
                parent->left = nullptr;
            }
            else if (parent->right == deleteTarget) {
                parent->right = nullptr;
            }   
            delete deleteTarget;
            return;
        }

        // 자식노드가 왼쪽 하나만 있을 때
        if (deleteTarget->right == nullptr && deleteTarget->left != nullptr) {
            if (!parent) {
                this->root = deleteTarget->left;
                delete deleteTarget;
            }
            else {
                if (parent->left == deleteTarget) {
                    parent->left = parent->left->left;
                }
                else if (parent->right == deleteTarget) {
                    parent->right = parent->right->left;
                }
                delete deleteTarget;
            }
            return;
        }
        // 자식노드가 오른쪽 하나만 있을 때
        else if (deleteTarget->right != nullptr && deleteTarget->left == nullptr) {
            if (!parent) {
                this->root = deleteTarget->right;
                delete deleteTarget;
            }
            else {
                if (parent->left == deleteTarget) {
                    parent->left = parent->left->right;
                }
                else if (parent->right == deleteTarget) {
                    parent->right = parent->right->right;
                }
                delete deleteTarget;
            }
            return;
        }
        // 자식노드가 두 개가 있을 때
        else {
            Node* tmp;
            cursor = deleteTarget->right;
            if (cursor->left) {
                while (cursor->left) {
                    tmp = cursor;
                    cursor = cursor->left;
                }

                int tmpValue = tmp->left->value;
                tmp->left->value = deleteTarget->value;
                deleteTarget->value = tmpValue;

                delete tmp->left;
                tmp->left = nullptr;
            }
            else if (cursor->right) {
                while (cursor->right) {
                    tmp = cursor;
                    cursor = cursor->right;
                }

                int tmpValue = tmp->right->value;
                tmp->right->value = deleteTarget->value;
                deleteTarget->value = tmpValue;

                delete tmp->right;
                tmp->right = nullptr;
            }
            return;
        }
    }

    void printTree() {
        this->_preorderTraversal(this->root);
        std::cout << std::endl;
    }
};

#include <iostream>
#include "datastructure/BinarySearchTree.h"

int main() {

    BinarySearchTree* bst = new BinarySearchTree();
    bst->insert(4);
    bst->insert(5);
    bst->insert(6);
    bst->insert(3);
    bst->insert(2);
    bst->insert(1);
    bst->insert(1); // 이미 있는 값입니다.

    std::cout << bst->find(3)->value << " 찾았습니다 !" << std::endl;

    bst->printTree();
    bst->remove(3);
    bst->printTree();
    bst->remove(1);
    bst->printTree();
    bst->remove(4);
    bst->printTree();
    bst->remove(2);
    bst->printTree();
    bst->remove(6);
    bst->printTree();

    return 0;
}