문제 설명📖

초기에는 LCA(Lowest Common Ancesotr)로 접근하여 N개의 노드 중 두 노드(A, B) 선택하여 LCA를 찾고 LCA 부터 루트 노드까지의 경로 + LCA 부터 A 노드 까지 경로 + LCA 부터 B 노드까지 경로를 더해 답을 구하려고 하였다.
하지만 이와 같이 풀 경우 두 개의 노드를 선택하는 데에만 O(N^2)이 걸리고 추가로 LCA를 구하는 데 O(N) 혹은 2의 제곱승 만큼 띄어넘는 방식을 사용하여 O(logN)이 걸린다면 총 O(N^3) 혹은 O(N^2logN)이 걸리게 되어 N의 입력 범위가 300000인 이 문제에서는 시간초과가 나게 된다. 이 때문에 머리를 싸매다가 구글링을 통해 해결하였다.
풀이 방법✏️
처음 문제를 읽게 되면 "모든 가능한 i, j의 쌍에 대해서" 라는 문구 때문에 자연스레 i, j 노드를 선택 후 문제에서 요구하는 걸 찾는 방법을 고민하게 된다. 그러면 자연스레 위에서 이야기했듯이 LCA를 떠올리게 되고 이는 결국 시간초과를 맞이한다. 그래서 이 문제를 풀기 위해서는 노드가 아닌 간선에 입장에서 자신이 i, j 쌍을 골랐을 때 총 몇 번 사용되는 지를 떠올려야 한다.
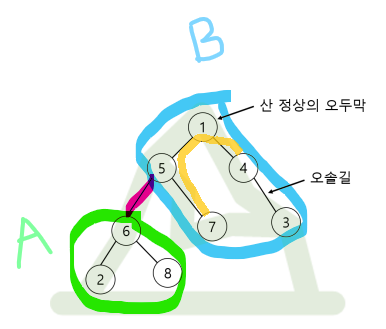
위 그림에 빨간 색으로 칠해진 간선에 입장에서 보았을 때 트리에서 두 노드를 선택하는 모든 경우의 수는 3가지로 구분된다.
- A, B 영역에서 각각 하나의 노드를 선택하는 경우
- A 영역에서 두 노드 모드 선택하는 경우
- B 영역에서 두 노드 모드 선택하는 경우
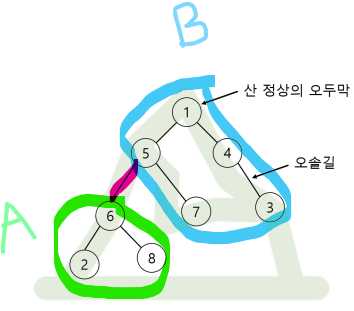
먼저 1번 경우를 고려하여 A 영역에서 2번, B 영역에서 3번을 선택했다고 가정해보자.
이 경우에는 위 그림과 같이 A 영역의 노드에서 B 영역의 노드를 이어주기 위해서 당연히 빨간 간선이 사용될 것이다.
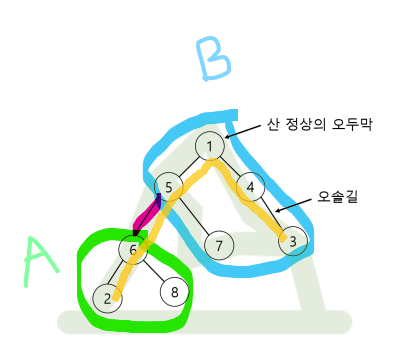
다음으로 2번 경우를 고려하여 A 영역에서 2번, 8번을 선택했다고 가정해보자. 이 경우에는 두 노드를 이을 때는 항상 루트 노드를 거쳐야 한다는 조건에 의해 위 그림과 같이 빨간 간선이 사용될 것이다.
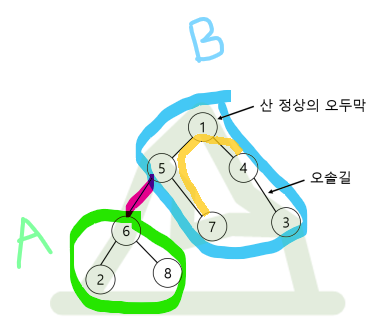
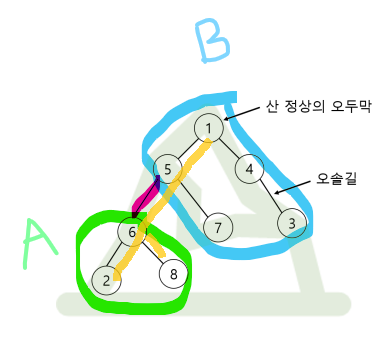
마지막으로 3번 경우를 고려하여 B 영역에서 7번, 4번을 선택한다고 가정해보자. 이 경우에는 루트 노드를 거쳐서 이어준다고 하더라도 위 그림과 같이 빨간 간선을 사용하지 않게 된다.
위 세가지 경우를 통해 우리는 트리에서 두 노드를 골랐을 때 빨간 간선이 사용 되는 경우의 수는 "모든 노드에서 두 노드를 고르는 경우(nC2) - 3번 경우"임을 알 수 있다. 이 계산을 모든 간선에 적용하게 되면 문제에서 원하는 모든 가능한 i, j의 쌍의 다양성의 총 합을 계산할 수 있다.
이제 남은 건 특정 간선을 선택하였을 때 B 영역에 속하는 노드가 몇 개인지를 구하기만 하면 되는데 이는 두 가지 과정으로 구성된다.
- DFS를 통해 루트 노드 부터 리프 노드까지 탐색해나가며 각 노드를 루트로 하는 서브트리에 포함된 총 노드 수 를 미리 구한다.
- 이후 앞서 구한 값을 바탕으로 전체 노드 수에서 선택한 간선의 도착지(더 높은 level의 노드)를 루트 노드로 하는 서브트리의 총 노드 수를 빼주면 B 영역에 속하는 노드의 개수를 구할 수 있다.
소스 코드(feat. 알찬 주석)⌨️
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.StringTokenizer;
public class BJ_20188 {
static int N, variety;
static List<Integer>[] tree;
static int[] subTree;
static boolean[] visited;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
tree = new List[N + 1];
for (int i = 0; i < N + 1; i++) {
tree[i] = new ArrayList<>();
}
subTree = new int[N + 1]; // subTree[i] : i 번째 노드를 루트노드로 하는 서브트리에 포함되는 노드의 수
for (int i = 1; i <= N; i++) { // 자기 자신을 무조건 포함하기 때문에 1로 초기화
subTree[i] = 1;
}
for (int i = 0; i < N - 1; i++) { // 인접리스트로 트리 표현
StringTokenizer st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
tree[start].add(end);
tree[end].add(start);
}
visited = new boolean[N + 1];
visited[1] = true;
DFS(1); // 루트 노드부터 dfs 탐색
// 주어진 서브 테스크에 따르면 루트 노드를 제외한 모든 노드는 부모로 가는 간선을 하나씩 지니게 된다.
// 따라서 2번 노드 위로 뻗어 나가는(부모로 가는) 간선 부터 마지막 노드 위로 뻗어 나가는 간선까지 순회하면 모든 간선을 고려하게 된다.
long variety = 0;
for (int i = 2; i <= N; i++) {
int restNodeCnt = N - subTree[i]; // 현재 선택한 간선을 사용하지 않는 조합을 이루는 노드의 개수
variety += nC2(N) - nC2(restNodeCnt);
}
System.out.println(variety);
}
private static long nC2(int n) { // nC2를 구해주는 메소드, n^2이 int를 초과하므로 long으로 선언
return (long) n * (n - 1) / 2;
}
private static int DFS(int cur) { // 깊이 우선 탐색을 통해 루트 노드 부터 리프 노드까지 내려가며 subTree 배열에 값을 채운다.
for (Integer next : tree[cur]) { // 자식 노드 탐색
if (visited[next]) { // 이미 방문한 곳이라면 continue(양방향 그래프이기 때문에 부모 노드로 다시 올라가는 걸 방지)
continue;
}
visited[next] = true;
subTree[cur] += DFS(next); // 서브트리 내 노드 개수 갱신
}
return subTree[cur];
}
}
- 문제 링크 : 등산 마니아
- 참고 : 백준 20188번: 등산 마니아