Advanced 자료구조(Data structure)2

그래프(Graph)

그래프란?
상하위의 개념없이 연결되어있는 객체 간의 관계를 표현한다. 노드(정점Vertex)와 노드들을 연결하는 간선(Edge)로 구성된다. 따라서 기본적으로 루트, 부모-자식의 개념이 없다
그래프의 특성
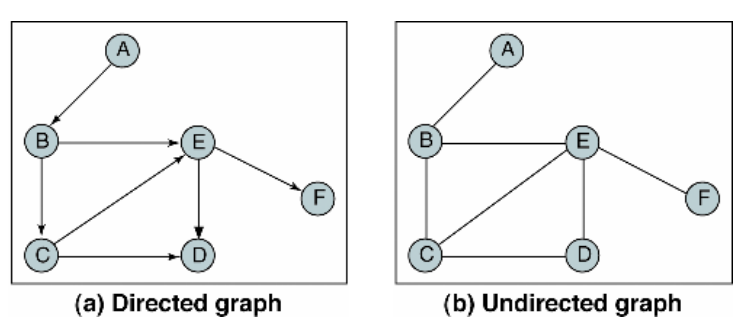
(1) 그래프는 방향이 있을수도 있고 (Directed) 없을수도 있다. (Undirected)

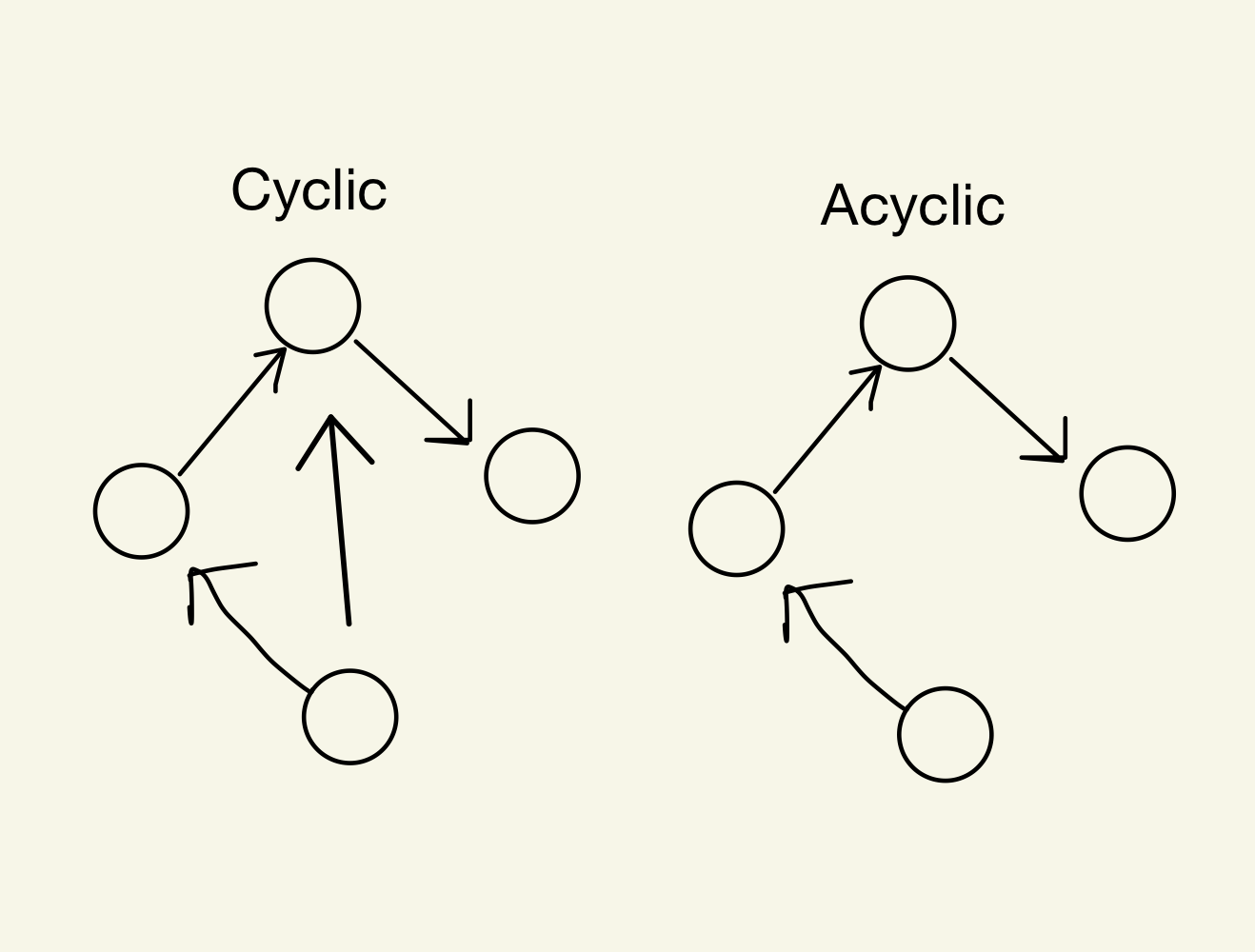
(2) 그래프 내부에 써클이 있을수도 있고 (cyclic) 없을수도 있다. (Acyclic)

그래프를 표현하는 방법 // Adjacency = 인접한
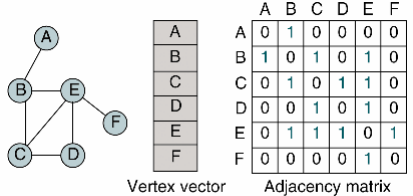
(1) 이차원배열 (Adjacency Matrix)

• 그래프를 0과 1를 이용하여 표로 표현
  
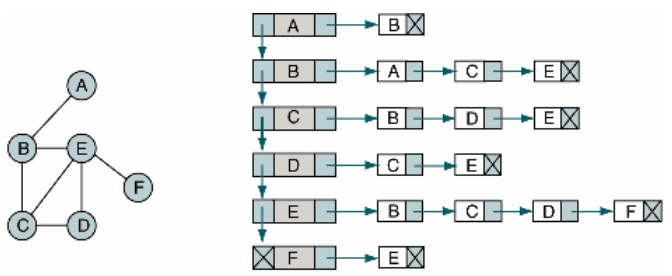
  (2) 리스트 (Adjacency List)
• 그래프를 연결리스트로 표현
  1 - 2 - 3 - 4
  2 - 1
  3 - 1 - 4
  4 - 3
  Edge가 m개일때, 총 노드의 갯수는 2m개이다.

트리(Tree)

트리 = 하나이상의 Child를 가진 계층구조 , 마지막 노드 (leaf)는 child를 가지지 않음
트리는 그래프의 한 종류.
1. 트리의 종류
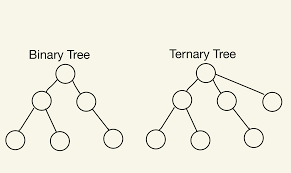
(1) child node가 2개이하로 붙을경우 이진트리 (binary tree)
(2) child node가 3개이상 붙을경우 삼진트리 (ternary tree)

2. 이진트리의 종류
(1) Binary Tree
다른조건없이 노드의 child가 2개이하.
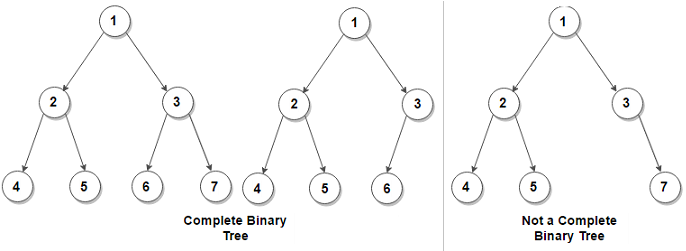
(2) Complete Binary Tree
모든 노드들이 왼쪽부터 채워져있는 이진트리

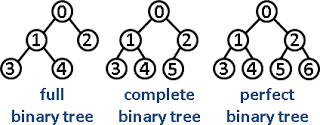
(3) Full Binary Tree
부모 노드가 자식노드를 2개 모두 가지거나 자식노드를 1개도
안갖는 이진트리
(4) Perpect Binary Tree
모든 부모노드가 자식노드를 2개 가지고있는 이진트리
노드의 level가 n일때 노드의 갯수는 2의 n승 -1개

(5) Binary search tree
부모 노드의 왼쪽 child노드와 그 자식노드들은 부모노드보다 작아야하고, 부모노드의 오른쪽 child노드와 그 자식노드들은 부모노드보다 커야한다.

3. Balanced (균형)
노드의 수가 정확히 일치하지않아도 한쪽으로만 크게 치우쳐져 있지않으면 Balance가 맞다고 표현하고 한쪽으로 치우쳐져 있는 경우 UnBalanced라고 한다.
Balanced를 갖는 트리
(1) Red-black tree
(2) Avl tree

4. 이진트리의 순회방법
(1) 중위순회 (Inorder)
Root를 중간에 순회한다. (Left-Root-Right)
(2) 전위순회 (Preorder)
Root를 제일 먼저 순회한다. (Root-Left-Right)
(3) 후위순회 (Postorder)
Root를 제일 나중에 순회한다. (Left-Right-Root)

그래프(Graph)와 트리(Tree)의 차이점