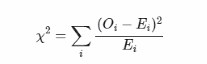
검정통계량?

-어느 가설이 맞는가를 판정할 때 기준이 되는 값

• 평균차이가 크다 표본 비율의 값이 크다 등 이는 상수가 아니라 확률 변수이다. 그러므로 언제든지 틀릴 가능성은 존재한다.
• 가설검정은 모집단의 모수가 이럴 것이다 라는 가설을 다루며 p값을 사용해서 귀무-대립가설을 설정한다.
• 가설이 타당한지를 파악하기 위해 계산을 할 때는 모수를 사용할 수 없다 그래서 통계에서는 표본통계량으로 계산을 한곤 하는데 이 표본통계량을 가설검정에서는 검정통계량이라고 부른다.

집단과 집단 사이가 독립인지 아닌지 서로 관련이 있는지 없는지 또는 집단이 하나 있을 시 데이터가 적합한지 아닌지 가설검정을 할 수 있다.

카이제곱검정

-카이제곱분포는 데이터의 분산이 퍼져있는 모습을 분포로 만든 것

chi2 = sum((실제값 - 기대값)^2 / 기대값)

• 적합도 검정과 교차분석을 이용할 때 카이제곱분포를 이용하는 경우가 많다.
• 빈도의 차이를 확인하는 검정
• 교차분석. 빈도수를 표현할 수 있다.
• 일원카이제곱
  • 변수(변인)가 하나
  • 변수들의 집단이 적합한 데이터로 구성되어있는지 아닌지 확인
• 이원카이제곱
  • 변수가 두개

수식

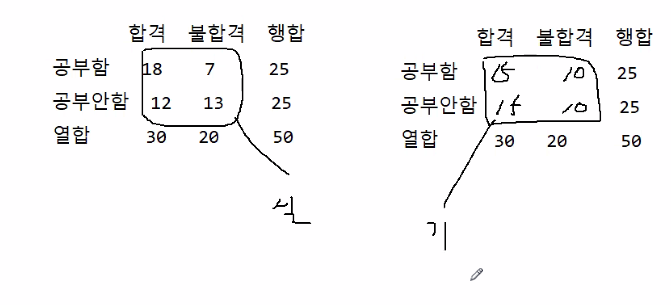
기대값(기대도수)구하기

(행의합/전체표본수x열의합/전체표본수)x전체표본수
기대값 = 각행의 주변합 * 각 열의 주변합 / 총합(전체표본수)

성별과 커피 브랜드의 종류가 있을 때 성별에 따라서 커피 브랜드의 차이가 있느냐 없느냐를 교차분석을 사용해 알아낼 수 있다.