✔️ Sort
오름차순/내림차순
package Sort;
import java.util.*;
public class practiceSort {
public static void main(String[] args) {
List<Integer> list = new LinkedList<>();
Random r = new Random();
for(int i = 0; i < 10; i++) list.add(r.nextInt(50));
System.out.println("Before sorting" + list);
list.sort(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o1.compareTo(o2);
}
});
System.out.println("After sorting" + list);
}
}
실행결과

1. Bubble Sort
- 정렬 알고리즘 중 가장 단순한 알고리즘, 비효율적임
- 동작 방식 : 인접한 두 요소간의 대소 비교 진행
- 시간 복잡도(최고, 평균, 최악) : O(n^2)
- 공간복잡도 : O(n)
2. Insertion Sort
- 알고리즘이 동작하는동안 계속해서 정렬이 진행되므로 반드시 맨 왼쪽 index까지 탐색하지 않아도 됨
- 동작 방식 : 정렬을 진행할 원소의 index보다 낮은 곳에 있는 원소들을 탐색하며 알맞은 위치에 삽입함, 첫 번째 index는 비교할 원소가 없어서 두 번째 index부터 시작함
- 시간 복잡도 : O(n)
- 공간복잡도 : O(n)
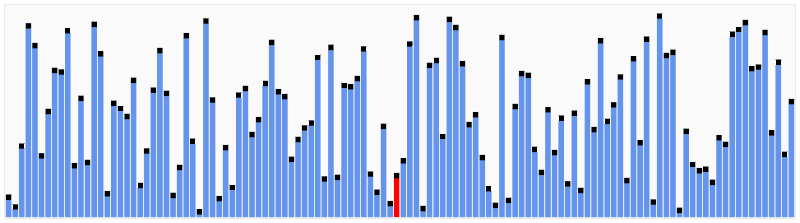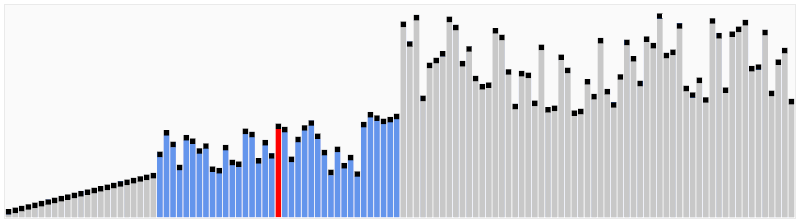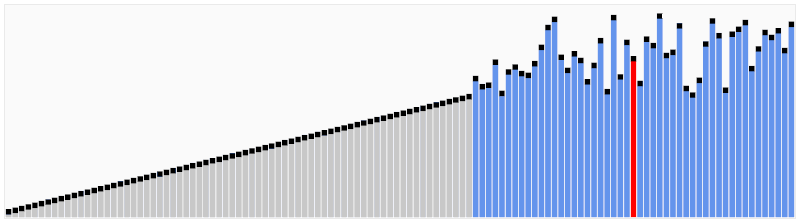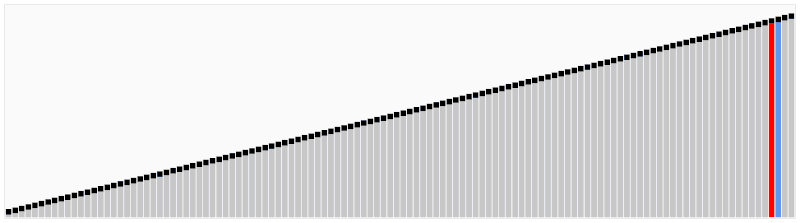
3. Selection Sort
- 배열에서 최소값을 반복적으로 찾아 정렬하는 알고리즘, 비효율적임
- 동작 방식 : 주어진 배열에서 최소값을 찾음 -> 최소값을 맨 앞의 값과 바꿈 -> 바꿔준 맨 앞 값을 제외한 나머지 원소를 동일한 방법으로 바꿈
- 시간 복잡도(최고, 평균, 최악) : O(n^2)
- 공간복잡도 : O(n)
4. Quick Sort
- 분할정복과 재귀 알고리즘을 사용하는 알고리즘, 정렬 될 기준 원소인 피봇 사용
- 시간 복잡도(최고, 평균, 최악) : O(nlogn)
- 공간복잡도 : O(n)
- 동작 방식 : 우선 피벗을 통해 정렬 → 영역을 쪼갬
5. Merge Sort
- 분할정복과 재귀 알고리즘을 사용하는 알고리즘
- 시간 복잡도(최고, 평균, 최악) : O(nlogn)
- 공간복잡도 : O(n)
- 동작 방식 : 영역을 쪼갤 수 있을 만큼 쪼갬 → 정렬
예제
Sortable.java
package Sort;
import java.util.Comparator;
import java.util.List;
public interface Sortable {
<T> List<T> sort(List<T> list, Comparator<T> comparator);
default <T extends Comparable> List<T> sort(List<T> list) {
return sort(list, Comparable::compareTo);
}
}
BubbleSort.java
package Sort;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.List;
public class BubbleSort implements Sortable {
@Override
public <T> List<T> sort(List<T> list, Comparator<T> comparator) {
List<T> copy = new LinkedList<>(list);
int size = copy.size();
for(int i = 0; i < size; i++) {
for(int j = i+1; j < size; j++) {
T d1 = copy.get(i);
T d2 = copy.get(j);
if (comparator.compare(d1, d2) > 0) {
copy.set(i, d2);
copy.set(j, d1);
}
}
}
return copy;
}
}
InsertionSort.java
package Sort;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.List;
public class InsertionSort implements Sortable {
@Override
public <T> List<T> sort(List<T> list, Comparator<T> comparator) {
List<T> copy = new LinkedList<>(list);
int size = copy.size();
for(int i = 1; i < size; i++) {
T d1 = copy.get(i);
for(int j = i-1; j >= 0; j--) {
T d2 = copy.get(j);
if(comparator.compare(d1, d2) > 0) break;
copy.remove(j);
copy.add(j+1, d2);
}
}
return copy;
}
}
SelectionSort.java
package Sort;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.List;
public class SelectionSort implements Sortable {
@Override
public <T> List<T> sort(List<T> list, Comparator<T> comparator) {
List<T> copy = new LinkedList<>(list);
int size = copy.size();
for(int i = 0; i< size; i++) {
int minIndex = i;
T min = copy.get(i);
for(int j = i+1; j < size; j++) {
T d = copy.get(j);
if(min == null || comparator.compare(min, d) > 0) {
minIndex = j;
min = d;
}
}
copy.remove(minIndex);
copy.add(i, min);
}
return copy;
}
}
QuickSort.java
package Sort;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.List;
import java.util.function.Predicate;
import java.util.stream.Collectors;
public class QuickSort implements Sortable {
@Override
public <T> List<T> sort(List<T> list, Comparator<T> comparator) {
List<T> copy = new LinkedList<>(list);
return quickSort(copy, comparator);
}
private <T> List<T> quickSort(List<T> list, Comparator<T> comparator) {
if(list.size() <= 1) return list;
T pivot = list.remove(list.size() / 2);
List<T> lesser = quickSort(sublist(list, (d) -> comparator.compare(pivot, d) > 0), comparator);
List<T> greater = quickSort(sublist(list, (d) -> comparator.compare(pivot, d) <= 0), comparator);
return new LinkedList<>() {{
addAll(lesser);
add(pivot);
addAll(greater);
}};
}
private <T> List<T> sublist(List<T> list, Predicate<T> filter) {
return list.stream().filter(filter).collect(Collectors.toList());
}
}
MergeSort.java
package Sort;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.List;
public class MergeSort implements Sortable {
@Override
public <T> List<T> sort(List<T> list, Comparator<T> comparator) {
List<T> copy = new LinkedList<>(list);
return mergeSort(copy, comparator);
}
private <T> List<T> mergeSort(List<T> list, Comparator<T> comparator) {
if(list.size() <= 1) return list;
int mid = list.size()/2;
List<T> left = sort(list.subList(0, mid), comparator);
List<T> right = sort(list.subList(mid, list.size()), comparator);
List<T> merged = new LinkedList<>();
while(!left.isEmpty() || !right.isEmpty()) {
if(left.isEmpty()) {
merged.addAll(right);
break;
}
if(right.isEmpty()) {
merged.addAll(left);
break;
}
T leftFirst = left.get(0);
T rightFirst = right.get(0);
if(comparator.compare(leftFirst, rightFirst) < 0) {
merged.add(left.remove(0));
} else {
merged.add(right.remove(0));
}
}
return merged;
}
}
SortTest.java
package Sort;
import java.util.Arrays;
import java.util.List;
import org.junit.jupiter.api.Test;
import static org.junit.jupiter.api.Assertions.assertEquals;
public class SortTest {
private List<Integer> getProblemList() {
return Arrays.asList(10, 9, 8, 7, 6, 5, 4, 3, 2, 1);
}
private List<Integer> getAnswerList() {
return Arrays.asList(1, 2, 3, 4, 5, 6, 7, 8, 9, 10);
}
@Test
void bubbleSort() {
List<Integer> list = getProblemList();
List<Integer> sorted = new BubbleSort().sort(list);
assertEquals(getAnswerList(), sorted);
}
@Test
void insertionSort() {
List<Integer> list = getProblemList();
List<Integer> sorted = new InsertionSort().sort(list);
assertEquals(getAnswerList(), sorted);
}
@Test
void selectionSort() {
List<Integer> list = getProblemList();
List<Integer> sorted = new SelectionSort().sort(list);
assertEquals(getAnswerList(), sorted);
}
@Test
void quickSort() {
List<Integer> list = getProblemList();
List<Integer> sorted = new QuickSort().sort(list);
assertEquals(getAnswerList(), sorted);
}
@Test
void mergeSort() {
List<Integer> list = getProblemList();
List<Integer> sorted = new MergeSort().sort(list);
assertEquals(getAnswerList(), sorted);
}
}
실행결과

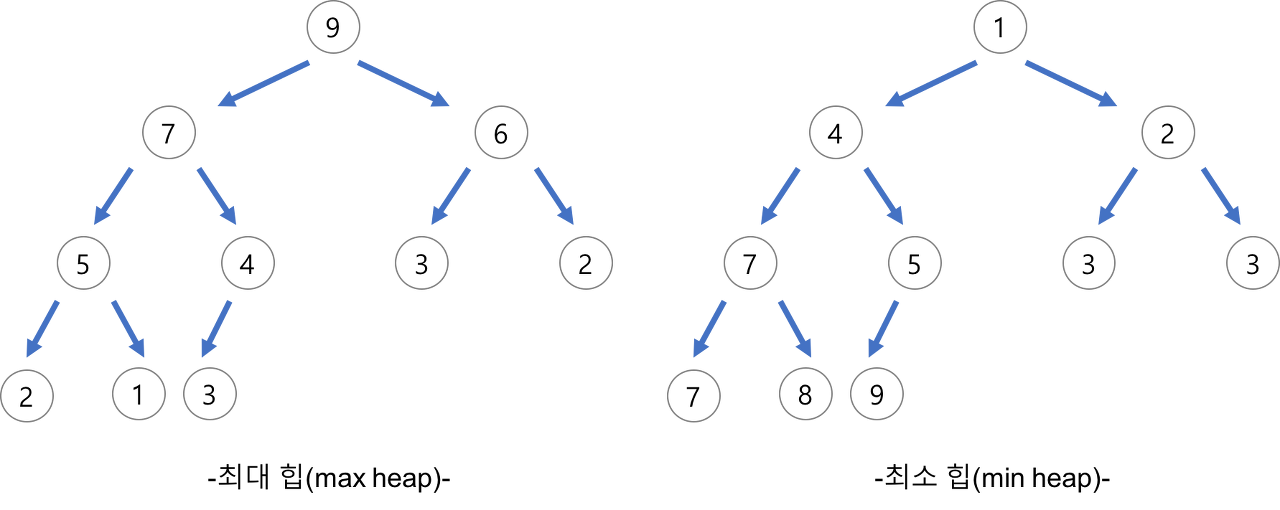
6. Heap Sort
- 완전 이진 트리를 기본으로 하는 힙 자료구조를 기반으로 한 알고리즘
- 시간 복잡도(최고, 평균, 최악) : O(nlogn)
- 공간복잡도 : O(n)
- 동작 방식 : 최대 힙 구성 -> 현재 힙 루트는 가장 큰 값이 존재함. 루트의 값을 마지막 요소와 바꾼 후, 힙의 사이즈 하나 줄임 -> 힙의 사이즈가 1보다 크면 위 과정 반복
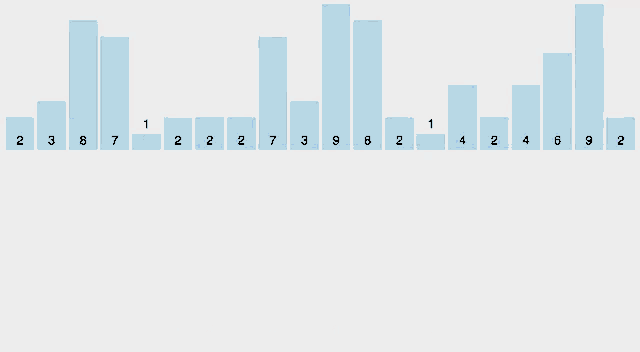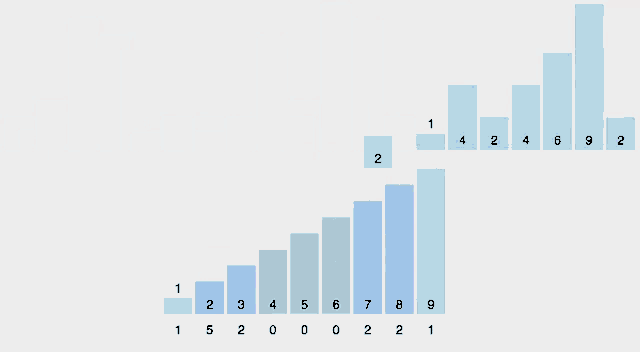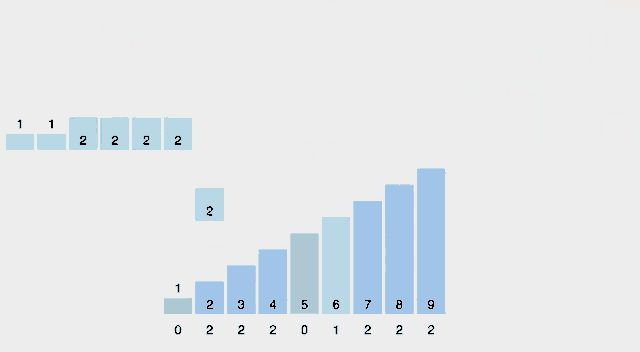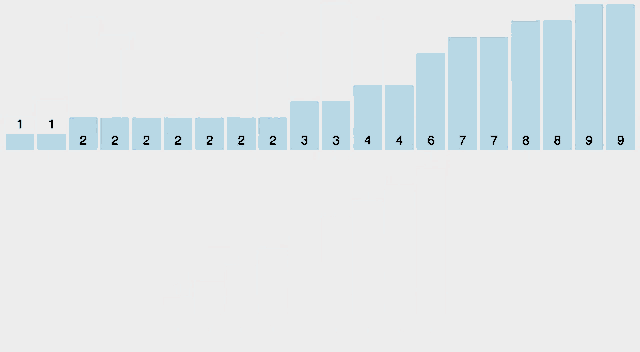
7. Radix Sort
- 데이터를 구성하는 기본 요소(Radix)를 이용하여 정렬하는 알고리즘
- 시간 복잡도(최고, 평균, 최악) : O(d * (n + b)) -> d는 정렬할 숫자의 자릿수, b는 10
- 공간복잡도 : O(n)
- 동작 방식 : 정렬하고자 하는 수의 낮은 자리 수를 차례대로 확인하여 정렬

8. Counting Sort
- 시간복잡도를 O(n)으로 낮추기 위해 도입된 정렬, 메모리 낭비가 심함
- 시간 복잡도(최고, 평균, 최악) : O(n + k) -> k는 배열에서 등장하는 최대값
- 공간복잡도 : O(k) -> k만큼의 배열을 만들어야 함
- 동작 방식 : 배열에 존재하는 원소 별 개수를 세어 정렬
위 내용은 블로그1, 블로그2를 참고하였습니다.