
✔️ Graph(그래프)
- 정점(Vertex)과 간선(Edge)로 이루어짐, 비선형 자료구조 중 하나
1. 그래프의 종류
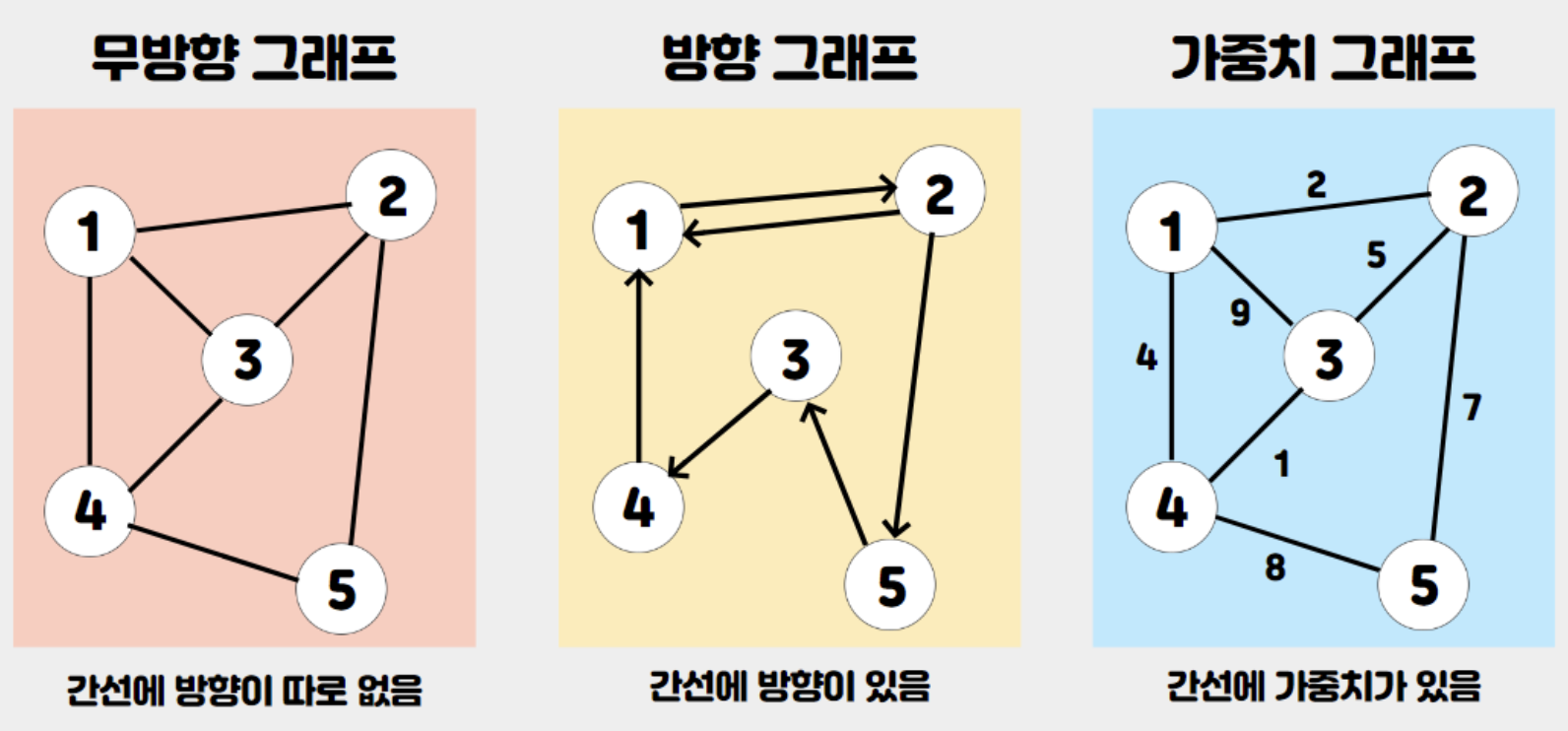
2. 그래프 구현 방법
- (1) 인접 행렬
- (2) 인접 리스트
인접 행렬 예제
Connection.java
package MatrixGraph;
public class Connection<T> {
private Node<T> node;
private int weight;
public Connection(Node<T> node, int weight) {
this.node = node;
this.weight = weight;
}
public Node<T> getNode() {
return node;
}
public int getWeight() {
return weight;
}
}Node.java - 제네릭 타입 T 사용
package MatrixGraph;
import java.util.LinkedList;
import java.util.List;
import java.util.Objects;
class Node<T> {
private T data;
private List<Connection<T>> links;
private boolean visited;
public Node(T name) {
this.data = name;
this.links = new LinkedList<>();
}
public List<Connection<T>> connections() {
return links;
}
public void link(Node<T> node, int weight) {
links.add(new Connection(node, weight));
}
public void resetVisit() { // visited 초기화 -> 재사용 가능하게 함
this.visited = false;
}
public void visit() {
this.visited = true;
}
public boolean isVisited() {
return this.visited;
}
@Override
public String toString() {
return data.toString();
}
@Override
public boolean equals(Object o) {
if (this == o) return true;
if (o == null || getClass() != o.getClass()) return false;
Node node = (Node) o;
return Objects.equals(data, node.data);
}
@Override
public int hashCode() {
return Objects.hash(data);
}
}
Graph.java - BFS/DFS 함수 내장, 각 탐색 시작하기 전에 rest을 통해 visited 초기화
package MatrixGraph;
import java.util.*;
public class Graph<T> {
private List<Node<T>> nodes = new ArrayList<>();
public void addNode(Node<T> node) {
nodes.add(node);
}
public Node<T> getNode(int index) {
return nodes.get(index);
}
public void generate(int[][] matrix) {
for(int i = 0; i < matrix.length; i++) {
int[] row = matrix[i];
for(int j = 0; j < row.length; j++) {
if(row[j] == 0) continue;
nodes.get(i).link(nodes.get(j), row[j]);
}
}
}
public void reset() {
nodes.forEach(Node::resetVisit);
}
public Connection<T> BFS(Node<T> start, Node<T> target) {
reset();
Queue<Connection<T>> queue = new LinkedList<>();
queue.offer(new Connection(start, 0));
while(!queue.isEmpty()) {
Connection<T> conn = queue.poll();
Node<T> n = conn.getNode();
int weight = conn.getWeight();
n.visit();
if(n.equals(target)) {
return new Connection<>(target, weight);
}
n.connections().stream()
.filter(i -> !i.getNode().isVisited())
.filter(i -> !queue.contains(i))
.map(i -> new Connection(i.getNode(), i.getWeight() + weight))
.forEach(queue::offer);
}
return null;
}
public Connection<T> DFS(Node<T> start, Node<T> target) {
reset();
Stack<Connection<T>> stack = new Stack<>();
stack.push(new Connection(start, 0));
while(!stack.isEmpty()) {
Connection<T> conn = stack.pop();
Node<T> n = conn.getNode();
int weight = conn.getWeight();
n.visit();
if(n.equals(target)) {
return new Connection<T>(target, weight);
}
n.connections().stream()
.filter(i -> !i.getNode().isVisited())
.filter(i -> !stack.contains(i))
.map(i -> new Connection(i.getNode(), i.getWeight() + weight))
.forEach(stack::push);
}
return null;
}
}
Main.java
package MatrixGraph;
public class Main {
public static void main(String[] args) {
Graph<String> graph = new Graph<String>();
graph.addNode(new Node("A"));
graph.addNode(new Node("B"));
graph.addNode(new Node("C"));
graph.addNode(new Node("D"));
graph.addNode(new Node("E"));
graph.generate(new int[][] {
{ 0, 0, 0, 2, 0 },
{ 5, 0, 6, 0, 4 },
{ 0, 6, 0, 0, 0 },
{ 0, 0, 2, 0, 0 },
{ 0, 0, 0, 3, 0 }
});
Node a = graph.getNode(0);
Node target = graph.getNode(4);
var answer1 = graph.BFS(a, target);
System.out.println(String.format("BFS : %s (%d)", answer1.getNode(), answer1.getWeight())); // BFS : E(14)
var answer2 = graph.DFS(a, target);
System.out.println(String.format("DFS : %s (%d)", answer2.getNode(), answer2.getWeight())); // DFS : E(14)
}
}3. 인접 행렬과 인접 리스트 비교
| 항목 | 인접 행렬 | 인접 리스트 |
|---|---|---|
| 시간 복잡도 | O(N^2), (정점 N * N만큼 필요) | O(N) |
| 두 정점의 연결 여부 | graph[x][y] 의 값으로 한번에 확인 | graph 의 원소에서 y가 나올때까지 탐색 |
| 인접 노드 파악 여부 | N * N만큼 반복문 돌아 확인 | 각 리스트에 담겨있는 원소 확인 |
